一种采用蒙卡程序计算两群中子价值分布的方法①

安伟健 赵泽昊 霍红磊

(中国原子能科学研究院反应堆工程技术研究部 北京 102413)

在开展反应堆物理特性分析时，中子价值往往可提供重要的帮助。中子价值的求解在确定论程序中较为容易，只需对中子输运方程的共轭方程进行求解，其求解过程和中子通量密度的求解同样容易。然而，对于蒙特卡罗程序（简称蒙卡程序），中子价值的求解则相对较为困难。

中子价值的定义为：临界系统中，在某一位置投入某一能量和运动方向的中子，由该中子引起的对系统稳定功率的贡献，即为该中子的价值。美国的Hurwitz还指出：临界系统中，由1个中子引起的每代裂变次数在代数趋于无穷时（此时中子分布已趋于稳定）会趋于一定值，即为中子价值。根据该理论，国际上针对蒙卡程序陆续开发了几种中子价值计算方法，分别将反复裂变几率、下一代裂变几率或下一代裂变中子数目的统计结果作为中子价值；在国内，汪量子等曾以反复裂变几率作为中子价值，将该方法融入到MCNP以及多群蒙卡程序MCMG中，获得了很好的计算效果[1]。

本文基于对中子价值物理意义的认识，提出了一种采用蒙卡程序计算两群中子价值分布的新方法，并将该方法成功应用于实际的反应堆物理特性分析工作中，取得了较好的效果。

1 方法描述

文献[2]提出了一种求解燃料内两群中子平均价值的比值的方法。该方法基于对反应堆内中子行为的认识，画出了燃料内热群中子的输运流程图，见图1。图中，P0为燃料内热群中子的首次飞行逃脱几率，C为燃料内热群中子在碰撞时发生散射的几率，v2为热群中子的平均裂变中子数；Σ2f为热群中子的宏观裂变截面； Σ2a为热群中子的宏观吸收截面。

根据中子价值守恒原理，初始中子的价值应当等于其后代中子的总价值。图中，初始中子的后代中子可分为两部分：在燃料里被吸收产生新一代的中子，以及泄漏至燃料外的中子。因而图1可简化为图2的形式，并可建立关系式（1）。其中，PFF,2为燃料内热群中子在燃料内被吸收的几率，PFO,2为燃料内热群中子泄漏至燃料外的几率；和分别为燃料内热群及快群中子的平均价值，为燃料外热群中子的平均价值。由此即可得到燃料内外两区的两群中子平均价值之间的关系（对于非临界系统，keff不能省略，用以维持不同代的中子价值守恒）。

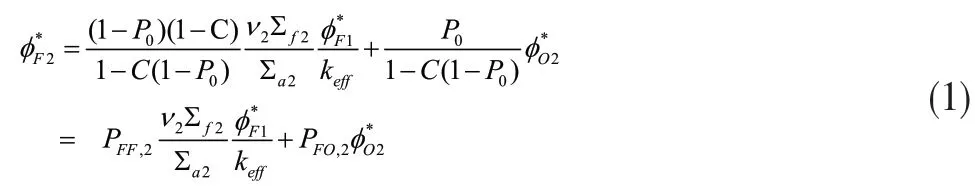
上述分析方法可进行拓展：若将反应堆划分为多个区，对各相邻区域分别开展分析，即可获得各区域的两群中子平均价值之间的关系式，进而可求得整个反应堆内的两群中子价值分布情况。以图3模型为例进行说明，将反应堆由内至外划分为三区，其中活性区分为两区（a区和b区），反射层为一区（c区）。

对a区的热群中子进行分析，可画出其输运简图（见图4），并建立关系式（2）。其中，va,2为a区热群中子的平均裂变中子数；Σa,f,2为a区热群中子的宏观裂变截面；Σa,a,2为a区热群中子的宏观吸收截面，其余各参数的命名规则可参考关系式（1）。

此外，对a区的快群中子进行分析，也可画出其输运简图（见图5），并建立关系式（3）。其中，Pa,12为a区快群中子慢化至热群的几率，其他参数命名规则可参考关系式（1）和（2）。

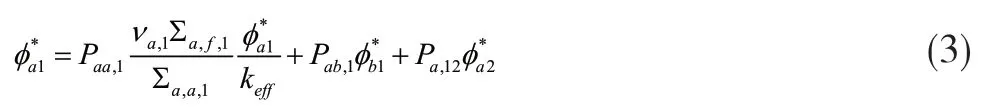
类似的，对b区的热群中子进行分析，也可画出其输运简图（见图6），并建立关系式（4）。参数命名规则可参考关系式（1）和（2）。

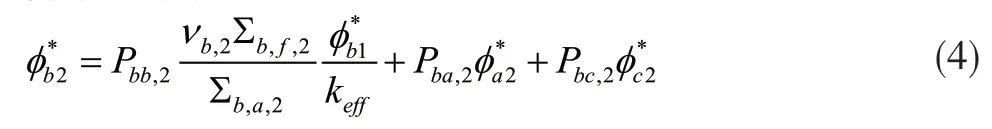
同样，对b区的快群中子、c区的热群及快群中子，均可分别建立对应的关系式如下：

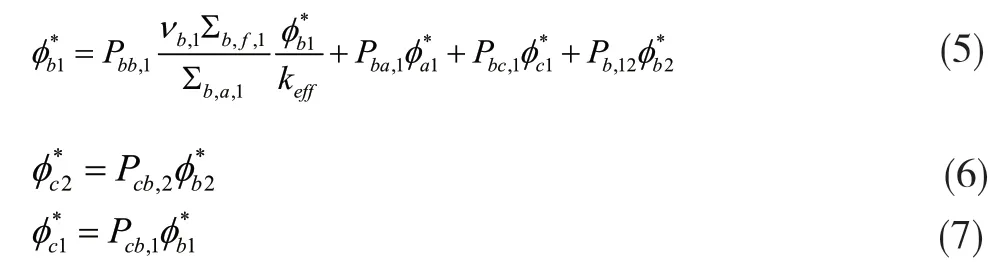
以上各式中的各项系数均可较容易由蒙卡程序MCNP计算并处理得到。将关系式（2）-（7）联立，可得6个关系式和6个未知量，实际计算过程中发现，该方程组并无法求出各未知量的确定解，因为计算过程中会出现两个等同的关系式，但可由其中任意5个关系式求出各未知量的相对值，也就是各区的两群中子平均价值之间的相对关系。以此为基础，若将反应堆较细致地划分为多个区域，采用该方法就可以获得整个反应堆内的两群中子价值分布情况。

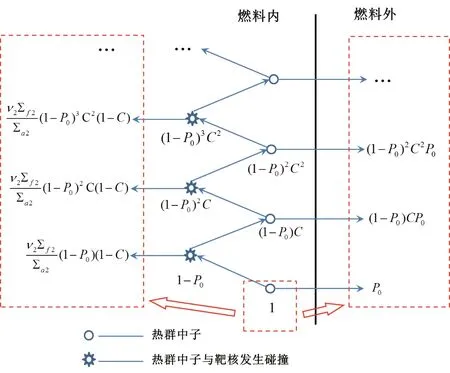
图1 燃料内热群中子的输运流程图

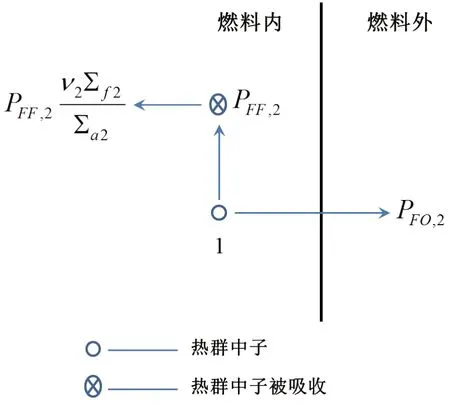
图2 燃料内热群中子的输运简图

2 方法应用

对一个采用CERMET燃料（燃料成分为W-60%UO2-6%Gd2O3，包壳为W-25%Re）的空间核反应堆的临界安全特性进行计算时发现：在反应堆进水的情况下，随着进水量的增加，系统的effk呈现出先增大后减小的特性。下面采用上述方法，从中子价值的角度对该现象进行分析。

首先，将该反应堆简化为球形模型，见图7，其中活性区半径为18cm，BeO反射层厚度为10cm。活性区进水时（假设水在活性区内均匀分布），系统effk随进水量的变化曲线见图8，在堆内水密度小于约0.03g/cm3时，k eff随进水量的增加而增大；而在堆内水密度大于约0.03g/cm3时，k eff将随进水量的增加而减小。

对该现象进行分析：活性区进水时，对系统的直接影响是增加了中子慢化性能，软化了堆芯的中子能谱。而中子能量的变化将影响其价值，也就是对effk的贡献，因而，考虑从中子价值的角度来进行研究，求解出堆内不同能群中子的价值分布，进而评估中子能谱的改变对effk的影响。

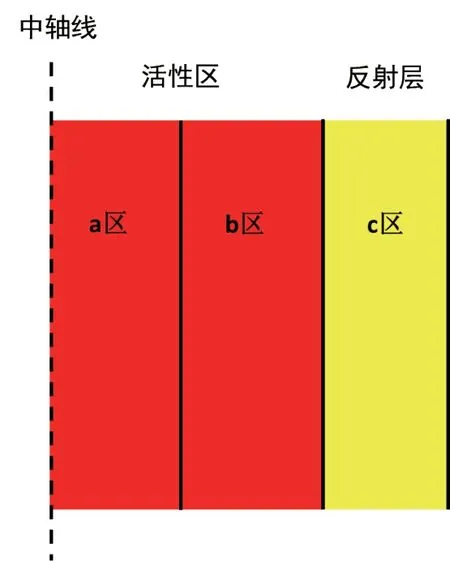
图3 反应堆分区模型

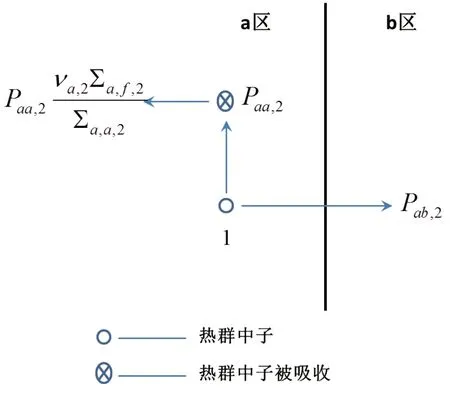
图4 a区热群中子的输运简图

图5 a区快群中子的输运简图

图6 b区热群中子的输运简图

由于该反应堆的中子能谱非常硬（无慢化剂，且燃料内含较多W、Re、Gd热中子毒物），热群中子所占份额极小，因此考虑以5.5 keV作为分界能，第二群中子包括共振中子和热中子，第一群中子则包括快中子和中能中子，裂变中子均为第一群中子。

将该球形反应堆模型按同心圆分成23区，其中活性区16区，反射层7区，从里到外用字母进行编号，见图9。在靠近活性区与反射层的交界处划分较细，这是由于该处中子通量密度随空间变化较快。

采用本文所提方法，对每个区的两群中子平均价值均可建立一个线性方程，这样一共可建立46个线性方程。而每个区均有两个未知量（也就是两群中子的平均价值），因此一共有46个未知量。在实际计算过程中会出现两个等同的关系式，可任选其一。这样，由45个方程可求解出46个未知量的相对值。令活性区最外层的第二群中子平均价值为1，将该线性方程组写为矩阵形式，可用MATLAB程序很容易求解。对于不同进水量的情况，计算结果如图10～12所示。

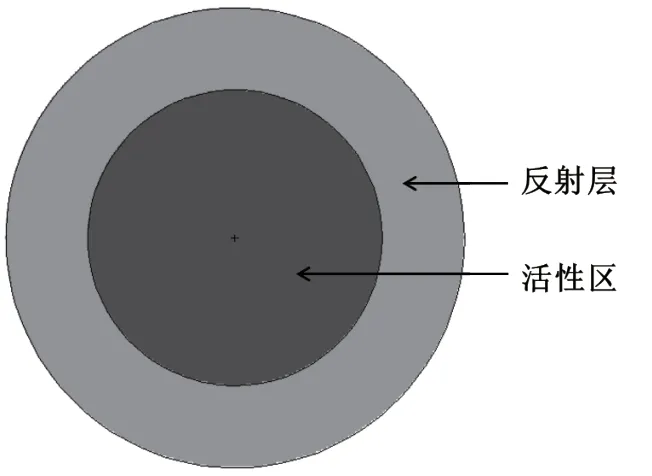
图7 反应堆简化球形模型

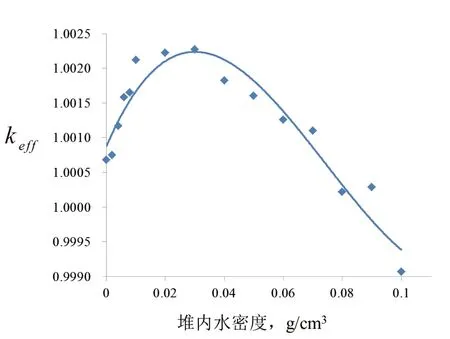
图8 反应堆 effk 随进水量的变化

图9 分区的计算模型

根据图10，活性区未进水时，在距离球心约0～8cm范围内，第一群中子的价值大于第二群中子，而在距球心8～18cm的区域（占活性区绝大部分区域），第一群中子的价值小于第二群中子，这使得在活性区进水导致能谱软化时，8～18cm的区域对反应性的正贡献占主导地位，从而使effk上升。再由图11和图12可以看出，随着进水量的增加，两群中子价值分布曲线的交叉点有明显的右移趋势。到水密度为0.1g/cm3时，活性区内绝大部分区域的第一群中子价值均大于第二群中子。这使得此时随着进水量的增加，keff将呈现下降趋势。这就解释了图8中effk随进水量的增加呈现出先增大后减小的现象。

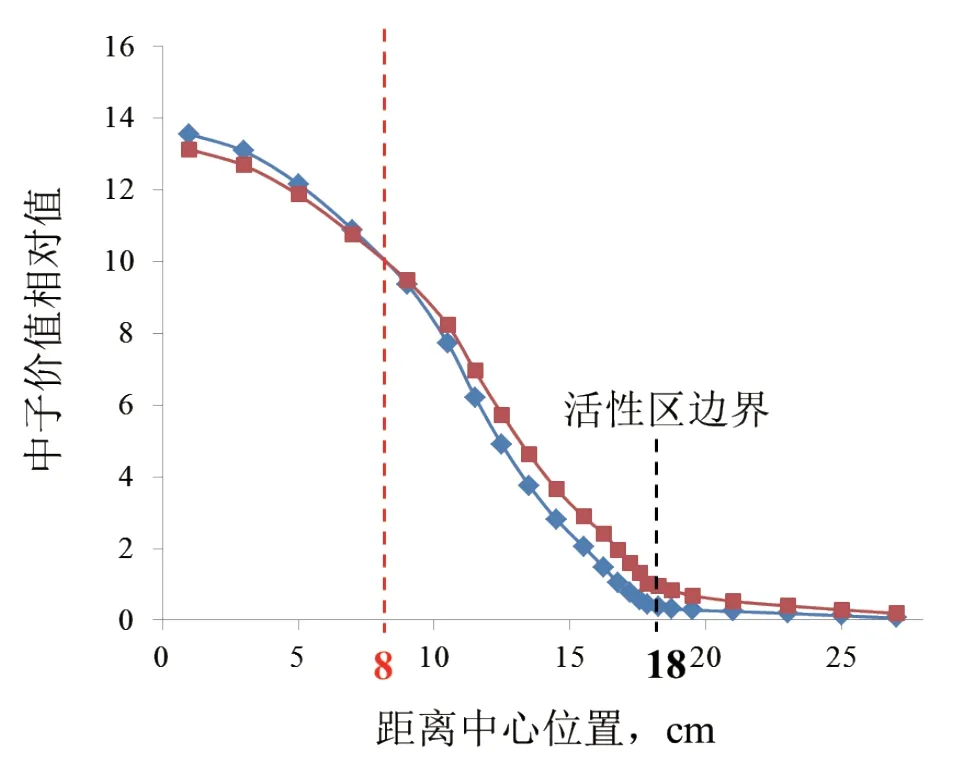
图10 堆芯两群中子价值相对分布（未进水）

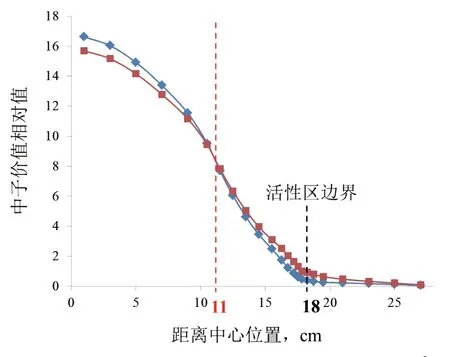
图11 堆芯两群中子价值相对分布（水密度0.03 g/cm3）

基于上述计算和分析结果，从物理方面可对该现象可作如下解释：在活性区靠近中心的区域，对中子价值起主导作用的是中子利用系数，由于W、Re、Gd等第二群中子毒物的存在，使得第二群中子的利用系数低于第一群中子，因此其价值低于第一群中子；在活性区靠外的区域，泄漏是影响中子价值的主导因素，第一群中子的泄漏率要比第二群中子高，导致第二群中子的价值高于第一群中子。在堆内未进水或进水量较少时，随着进水量的增加，中子的利用系数减小，不泄漏几率增大，后者对系统的影响大于前者，使得effk增大；在堆内进水量较多时，随着进水量的增加，中子的利用系数减小，不泄漏几率增大，此时前者占主导地位，使得effk减小。

3 结果验证

采用微扰方法对上述中子价值计算结果进行验证。具体如下：

CERMET燃料里包含一定量的Gd2O3。若对Gd的量作微小的调整，对中子通量密度的分布影响很小，可采用微扰方法计算反应性的变化量。该值也可通过计算调整前后的effk变化量来求得。若上述中子价值的计算结果正确，则这两种方法的计算结果应当相符。

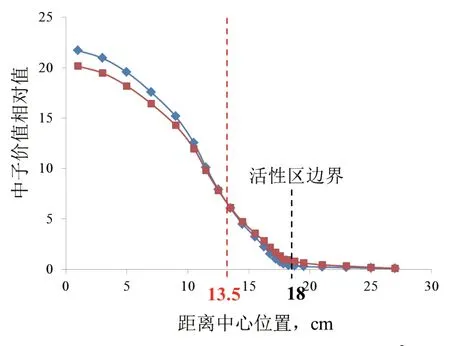
图12 堆芯两群中子价值相对分布（水密度0.1g/cm3）

将CERMET燃料中的Gd减少10%。按照微扰理论[3]，反应性的变化量应当等于这10%的Gd所吸收的中子价值与系统内中子总价值的比值：

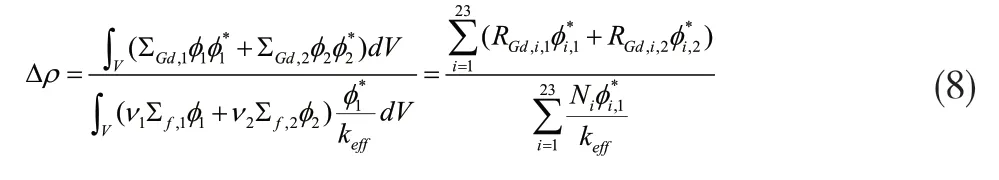
式中，ΣGd,1、ΣGd,2分别为Gd的宏观吸收截面，RGd,i,1、分别为第i区内Gd对第一群和第二群中子的吸收率，Ni为第i区燃料的裂变中子产生率。各参数均可由MCNP程序很容易算得。结合之前的计算结果，可算得由于Gd的减少所引起的反应性变化量为：另一方面，通过计算调整前后的effk变化量也可得到Δρ的数值，该方法的计算结果为：两种方法的计算结果差别仅为4.2%。这说明该方法的计算结果是合理可信的。

4 结语

针对一般蒙卡程序无法计算中子价值的问题，提出了一种采用蒙卡程序计算两群中子价值分布的新方法，并将该方法成功应用于实际反应堆的物理特性分析中。所存在的不足之处在于：由于手头上没有其他有效的中子价值计算程序，因此没能对中子价值分布的计算结果进行直接校验，而是通过微扰方法进行了间接的验证。