恒应变速率压缩中压实黄土结构特征试验研究

秦鹏举，宋志伟，王永宝，苗晨曦，马富丽，董晓强

(太原理工大学 土木工程学院，太原 030024)

随着“一带一路”和中西部开发等国家战略的实施，我国黄土地区的工程建设如火如荼。从世界范围内看，我国黄土分布面积最广、层厚最大、地层完整、地貌类型多而复杂，覆盖面积达64万km2，约占我国领土面积的6.6%，主要分布于我国黄河中、下游地区[1-2]。在工程实践中，如建筑、道路和桥梁地基，往往通过压实原状黄土比如重锤表层夯实、强夯等，来改善土体的力学性质，以增强土体的稳定。并且，压实黄土的力学性质决定工程的安全性。然而，如何快速准确地确定压实黄土能否满足建设工程需要，有必要进行深入研究。

变形黄土力学性质的确定通常采用分级加载的方法，测试过程中需要确定荷载分级、加载比等测试参数。然而，分级加载方法所用时间较长，并且所得压缩曲线为离散的点，不利于力学参数的确定，结果受荷载分级和加载比的影响较大。为了能够克服这些困难，有学者采用恒应变速率方法确定土的力学性质。恒应变速率方法是一种连续加载的方法，能快速、有效和标准地获取压缩曲线连续的点，从而更加准确地确定土的力学参数，此方法已初步用于非饱和土力学性质的研究中[3-5]。另外，恒应变速率方法更适合于容易受龄期影响或试样性质容易变化的土样的力学参数确定，以减少土样性质随时间变化对其力学性质的影响。但恒应变速率方法在非饱和土中的应用较少，需要进一步探索其适用性。

另外，土电阻率是表征土导电性的基本参数。土的电阻率特征受许多因素的影响，如孔隙率、孔隙形状、孔隙液电阻率、饱和度、固体颗粒成分、温度、结构特征等。同时，土电阻率法能够连续实时测量土体的电阻率值的变化，并且可以根据土体的形式变换测试电极的形状大小，容易满足测试中苛刻的要求，所用装置相对简单且无复杂的操作，具有方便、连续、快速、经济等优点。为此，电阻率法可用于土体的微观结构变形特征定量评价、测量水含量、分析土的颗粒组成，进而确定土的工程力学性质[6-11]。基于这些优点，电阻率法用于表征土样变形过程中土的性质。

为了研究快速确定压实黄土力学性质的方法，本文配置一定含水量的黄土粉末，并压实成一定尺寸圆柱状黄土试样，将电阻率电极置于试样顶底部，用于测量土样变形过程中电阻率的变化。而土样的压缩通过恒应变速率法进行测试，测试过程中保持试样含水量不变。试验结束后，对比分析试样压缩曲线及力学参数，分析电阻率值变化特征以表征土的性质。

1 试验材料与方法

1.1 土的基本性质

本次试验所用黄土取自太原东山地区，取土深度为4～5 m，土质比较均匀，呈黄色，坚硬状，其基本物理指标见表1，其中最大干密度和最优含水量由轻型标准击实试验确定。颗粒分布曲线见图1，根据《土的工程分类标准》(GB/T 50145-2007)[12]，试验所用黄土细粒含量超过50%，塑性指数Ip<10，可判定其为粉土。

表1 黄土基本物理指标Table 1 Basic physical properties of the soil

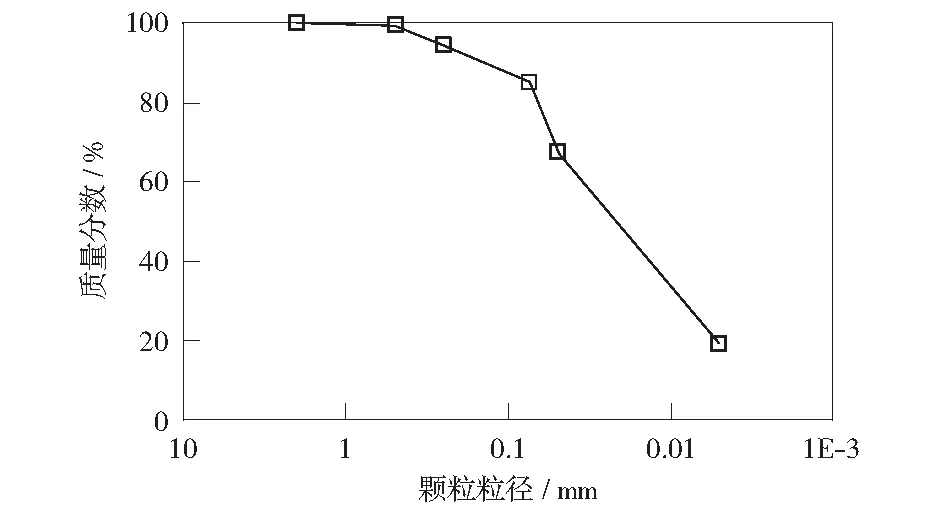
图1 土样颗分曲线Fig.1 Grain size distribution of sample

1.2 试样的制备

将采集的原状土晾干、碾碎，过2 mm标准筛，以准备所用黄土碎散土料。首先，为了与文献[11]对比，预计配置含水量(质量分数)为11.3%的土料，将配置好的土料封闭保存24 h，使水分均匀分布于土料中。烘干法确定配备好土料含水量为12.01%，而后，压制土样。根据压制试样的高度、干密度和所配土料含水量，将准备后的土料放置于试样环中，通过施加0.4 mm/min恒定位移速率来压制试样，直至试样高度达到10 mm，干密度达到1.39 g/cm3，停止压制试样，并静止30 min.而后，测量压制试样尺寸，至此试样压制完成。经测量所压制试样实际高度为9.755 mm，直径为64 mm，干密度1.424 g/cm3.试验完成后的含水量为11.84%，具体参数如表2所示。

表2 压实黄土初始参数Table 2 Parameters of the compacted loess soil

1.3 试验方法

图2为本研究所用仪器示意图。试样压制于试样环中，试样环材料是具有高强度、刚度的绝缘材料，其内径为64 mm，高度为10 mm.试样顶底两端各设置一片铜箔导体材料制成的横向电极，厚约0.05 mm，直径为20 mm，并有导线引出与电阻率测试仪相连。试样和横向电极夹于上下透水石之间，上透水石置于试样环内，下透水石尺寸大于试样环外径，承托试样环、电极和试样等。另外，紧贴着透水石在试样一侧为滤纸，未绘制于图2中。上透水石之上为金属上盖，承受加载架施加的荷载，并传递给试样。钢珠置于上盖之上以使荷载均匀作用于上盖之上。将试样环、透水石等置于金属水槽之中。试样顶端和底部的横向电极用于测量试样竖向电阻率。试验过程中也需要测量试样的横向电阻率，由贴近试样环内壁径向对称设置铜箔竖向电极实现，并且通过导线将电极与电阻率测试仪连接，电极的高度要高于试样高度，电极的宽度为3.5 mm，测量横向电阻率的所用电极如图2所示。试验过程中通过交替将横向和竖向电极与电阻率测试仪来测量试样的竖向和横向电阻率。

本次试验采用电阻率测试仪为TH2828A型号的LCR数字电桥，其基本精度为0.1%，频率范围为20 Hz～1 MHz，试验中使用的交流电频率为50 Hz～1 MHz，仪器有效量程高达100 MΩ，本文中用于测量压实黄土试样的阻抗模|Z|等参数，并用式(1)计算电阻率值。

ρ=|Z|·S/L.

(1)

式中：ρ为黄土电阻率，Ω·m；|Z|为阻抗模，Ω ；S为电极片面积，m2；L为电极片之间的距离，m.

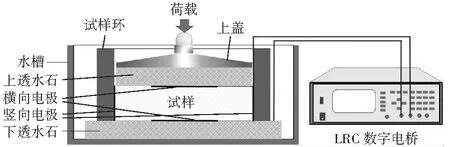
图2 试验装置示意图Fig.2 Schematic graph of test setup

将压制好的试样如图2所示安装，而后将水槽及内部部分放置于加载架上，施加恒应变速率0.005%·s-1，相应位移应变速率为0.06 mm/min，应变速率的选择应以较快的速度完成试验并减小或避免出现孔隙水压力为依据，参考文献[13]中应变速率取值。试验过程中将水槽内试验装置用速率带包裹以减少含水量变化。试验过程中同时记录试样压缩过程中试样竖向变形和相应施加的压力。

2 试验结果与分析

2.1 压缩曲线与压缩性指标

由图3可见，恒应变速率试验获取的压缩曲线数据点相对于分级加载数据点多，且数据数量可根据精度要求进行采集。另外，随着应力增大，应变随之增大。初期压力较小，压缩应变较小。当压力大于一定值后，压缩应变变形速率增大。变形曲线呈类似两段线形，是比较典型的重塑土的压缩曲线。根据压缩变形曲线的形状，可将曲线分为弹性压缩和塑性压缩部分。弹性部分压缩产生的变形较小，这部分的变形通常是土骨架的弹性变形。而当压缩黄土压缩曲线位于塑性压缩部分，压实黄土骨架发生塑性变形，即卸载后试样发生不可逆的压缩变形。在此阶段，土中与外部连通，气体会部分排出土样外部，土颗粒排列发生变化，土中孔隙受压后变小。可

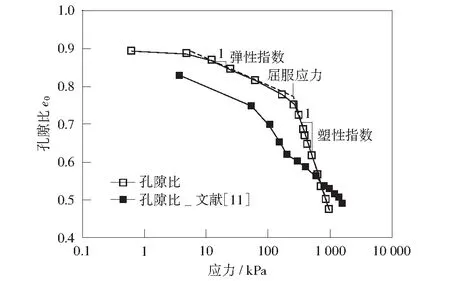
图3 应力-孔隙比曲线Fig.3 Curves of stress-void ratio

见，分级加载方法和恒应变速率方法获取压缩曲线形式基本相同，但由于初始孔隙比不同，两曲线弹性压缩阶段不同，在塑性压缩阶段压缩曲线出现交叉。

为了定量分析曲线的压缩情况，文中获取弹性压缩指数和塑性压缩指数，获取的方法参见文献[3]，即弹性部分压缩曲线的切线的斜率获取弹性压缩指数，塑性压缩曲线部分切线的斜率获取塑性压缩指数。弹性部分压缩曲线的切线和塑性部分压缩曲线的切线交点的应力为屈服应力，具体的参数获取方法示意图如图3所示。在确定力学参数过程中，恒应变速率试验获取点数较多，可以比较准确确定弹性压缩曲线和塑性压缩曲线的位置，但分级加载试验获取的压缩曲线数据较为离散，从而确定参数存在一些困难，甚至不准确。图4为根据本文试验和文献[11]压缩曲线所确定力学参数，可见弹性压缩指数小于塑性压缩指数，与图3两曲线确定的弹性压缩指数较为相近，反映在图3中为两压缩曲线弹性压缩阶段基本平行。另外，两压缩曲线获取的塑性压缩指数和屈服应力有所不同，即恒应变速率试验压缩曲线获取的塑性压缩指数和屈服应力较大，而分级加载试验压缩曲线所确定的塑性压缩指数和屈服应力较小。根据文献[14]，可以看到初始孔隙比不同压缩曲线基本平行。另外，根据文献[15]，可以看到相同初始孔隙比下，饱和原状土的压缩曲线在初始压缩阶段比重塑黄土靠右，对比本文中压缩曲线，可能是初始孔隙比和土的结构性的共同影响结果，反映在图3中为两曲线出现交叉。由此可见，恒应变速率法在确定土样力学参数方面确有其难得的优点。

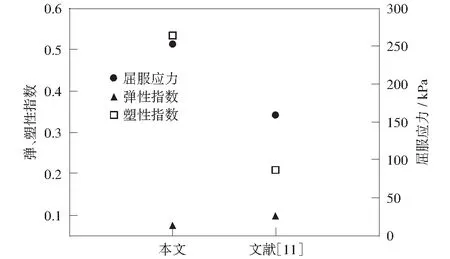
图4 力学参数Fig.4 Mechanical parameters

2.2 压实黄土电阻率特征

图5为应变-竖向电阻率关系，根据图5所示，压缩曲线可分为两个阶段：第一阶段，随着应力的增加，应变开始加大，电极被所施加荷载压紧，电极与试样之间的空气被挤出，进入试样电阻率测试阶段，土的密实度提高，孔隙体积减小，饱和度增大，部分孔隙水得以联通形成导电通道， 故电流路径明显增多，表现为电阻率急速降低；第二阶段，荷载逐渐增加，应变同步增大，土骨架发生错动，孔隙被填充，颗粒连接更加紧密，空气排出土外，土体更加密实，孔隙率减小，饱和度增大，在含水量不变情况下，孔隙水连通性加强，电流导通路径增多，电阻率值继续下降，但下降的速度明显放缓。根据文献[11]，还会出现第三阶段，即当荷载增大到一定程度，虽然应变同步增加，但是空气基本排出，饱和度增加幅度变小，孔隙水通路增长很少，导致电流路径增加不明显，电阻率值变化较小趋于稳定。另外，同一应力作用下，随着交变电流频率的增加，电阻率减小，试样表现出容性电阻的性质。此现象是由于在一定的电压下，电容器充放电过程中电容器电路中定向移动的电荷量为定值，电流的频率越高充放电的时间就越短，从而导电容器电路中电流越大，容抗越小。然而，500 kHz交流频率下取得的电阻率却高于其临近电流频率下的电阻率值，类似于共振现象即输入的电流频率和材料的固有频率相同，所得的电阻率最大，但这需要进一步的研究。

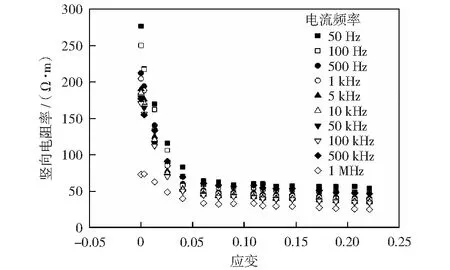
图5 应变-竖向电阻率关系Fig.5 Curves of stress-vertical electrical resistivity

图6为电流频率50 kHz下电阻率和应变之间的关系。图中电阻率分为竖向电阻率和横向电阻率。竖向电阻率与横向电阻率随应变增大而减小。竖向电阻率大于横向电阻率，这表明土的竖向结构和横向结构不同，即土存在各向异性。竖向电阻率初期随应变增大较快减小，随后幅度下降较慢，呈双线型的变化。横向电阻率随应变增大基本呈线型变化，未出现竖向电阻率初始快速下降段。这可能是由于试样受横向限制变形小甚至无变形，而竖向受压变形较大引起的。

图6 电阻率(50 kHz)-应变关系Fig.6 Curves of electrical resistivity (50 kHz)-strain

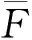
FV=ρV/ρw，FH=ρH/ρw.

(2)

(3)

(4)

(5)

根据图6中所示竖向和横向电阻率值，并且测量了50 kHz下水的电阻率为6.732 Ω·m，则根据公式(3)-(5)可以计算土样的平均结构因子、各向异性系数和平均形状因子。压实黄土压缩过程中应变是土样结构变化的宏观参量，因此建立结构参数与应变之间的关系，来讨论微观结构和宏观应变之间的关系。具体的结果分析如下：

土体压缩过程中伴随土结构调整以及新结构的形成，可分为土的竖向和横向结构变化。压缩过程中平均结构因子与应变的关系如图7所示。由图7可见，平均结构因子随应变增大而减小，其变化规律类似于竖向电阻率的变化规律，这是由于竖向结构因子占主导地位。平均结构因子减小主要由压缩过程中土样孔隙被压缩，孔隙率减小，饱和度逐渐增大，竖向结构单元发生较大变化引起。结构单元指包括颗粒排列、接触情况、土骨架状态、水分布状态等结构的单元。根据文献[15]，土受到击实或压实，土中较大直径的孔隙减少，较小直径的孔隙增多，表明土颗粒间接触面积增大，由点接触变成面接触状态，平均结构因子减小。平均结构因子随应变呈双线型变化，第一阶段平均结构因子减小较快，而第二阶段平均结构因子减小较慢，这表明随着压缩的不断进行，土体结构不断变化，密实度逐渐增大，压缩性越来越小，结构稳定性增加。应变的变化是土的微结构变化的宏观体现，影响着压实黄土在工程中的稳定性，通过测量土体的电阻率，利用平均结构因子与应变之间的线性关系，可评价压实黄土在工程中的稳定性。

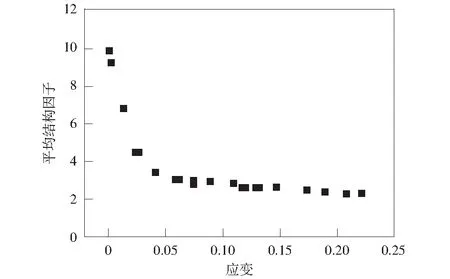
图7 平均结构因子与应变的关系Fig.7 Relationship between average structure factor and strain

压实黄土存在各向异性，表现为竖向结构和横向结构不同。由土电阻率获取的竖向和横向结构因子及其变化计算的各向异性系数及其变化规律可反映土体的各向异性。压实黄土压缩过程中的各向异性系数随应变的变化关系如图8所示。从图8可以看出，在初期压缩阶段，土的各向异性系数随着应变增大而明显减小，这可能由于竖向结构变化明显大于横向结构的变化；第二压缩阶段，各向异性系数趋于稳定。这可能由于土的横向结构变化受到环刀的限制，土的压缩变形主要引起竖向结构的变化，横向结构变形较竖向上的要小，而初始阶段竖向结构减小较快；土体在经过第一阶段的压缩后，其竖向结构变形已经达到一定的程度，此时土的竖向结构变化减小，横向方向上也变的相对密实，随着土的继续压缩，土的竖向结构变化和横向结构变化趋于稳定，从而导致各向异性系数趋于稳定。根据文献[17]，随着应力增大，静止侧压力系数由小增大。笔者认为静止侧压力系数可以反映出土在压缩过程中的各向异性，正是由于各向异性的存在导致静止侧压力系数小于1.从竖向和横向的比值关系看，本文中各向异性系数与静止侧压力系数呈倒数关系，随着应力增大均趋向于稳定，说明各向异性系数应变增大是合理的。

图8 各向异性系数与应变的关系Fig.8 Relationship between anisotropic index and strain

压实黄土压缩过程是伴随土的结构单元体变形、土体微观结构的调整与土颗粒间的胶结作用变化。压实黄土压缩过程中平均形状因子与应变的关系如图9所示。从图9可以看出，在第一压缩阶段，平均形状因子随应变增大而大幅度降低；在第二压缩阶段，平均形状因子随应变增大继续减小，但下降幅度减小；平均形状因子随应变变化基本呈双线型。根据文献[18]，黄土胶结材料主要包括碳酸钙、黏土矿物、有机胶体、易溶盐等。随着压缩孔隙中孔隙水增多，胶结材料溶解使胶结作用减小。黄土的压缩导致土的结构破坏，土的颗粒发生转动或者滑移，土颗粒间的胶结程度继续变弱，导致平均形状因子不断减小。毛细吸力随饱和度增大而减小，这也会导致随着应变的增大压实黄土的胶结作用减小。另外，根据胶结试样剪切波速表现，文献[19]发现橡胶-砂颗粒混合物颗粒间胶结作用在高应力条件下退化完全。这些均表明随着应变增大平均形状因子减小。平均形状因子与土颗粒间的胶结作用紧密相连，利用平均形状因子可定量分析土体压缩过程中土颗粒间的胶结作用的变化规律。

图9 平均形状因子与应变的关系Fig.9 Relationship between average shape factor and strain

3 结论

通过压实黄土恒应变速率压实试验以及压缩过程中的电阻率测试，研究了压实黄土压缩性质和与电阻率相关结构参数，包括平均结构因子、各向异性系数以及平均形状因子的变化规律，探讨了电阻率方法在土的恒应变速率压缩过程中的微结构变化研究中的应用。得出的主要结论如下：

恒应变速率方法可快速获取连续的压缩曲线点，压缩曲线可分为弹性压缩阶段、塑性压缩阶段。塑性压缩指数大于弹性压缩指数。另外，初始孔隙比和土的结构性对压缩曲线有影响，需要深入研究。

根据压实黄土竖向电阻率与应变之间的关系，可将土的压缩分为两个阶段。第一阶段竖向电阻率下降迅速，第二阶段竖向电阻率下降幅度减小。压实黄土竖向电阻率随应变的增大而减小，电流频率的升高基本呈减小趋势，500 kHz交流频率下取得的电阻率高于其临近电流频率下的电阻率值。横向电阻率随应变的增加而逐渐减小，竖向电阻率大于横向电阻率；另外，压缩过程中，平均结构因子和平均形状因子随着应变的增大而呈双线型减小，表明压实黄土孔隙率逐渐减小，土颗粒滑移或错动等重平衡过程中土样稳定性增加。各向异性系数随应变增大先减小随后趋于稳定，表明随着压缩，土样趋于稳定，竖向和横向结构单元变化速率趋于稳定。平均形状因子随着应变的增大而呈双线型减小，表明土样压缩过程中土颗粒间的胶结程度不断减弱。压缩过程中压实黄土的结构参数反映其微观结构的变化规律，可作为评价黄土力学性质的依据。