脑网络社团连接在轻度认知障碍分类中的应用

高 原，王 鑫，牛 焱，曹 锐，相 洁

(太原理工大学 a.信息与计算机学院，b.软件学院，太原 030024)

轻度认知障碍(mild cognitive impairment，MCI)是从正常衰老(normal control，NC)发展至阿尔茨海默病(alzheimer’s disease，AD)的中间状态，特点为有轻微的记忆和认知受损却未达到痴呆状态[1]。已有研究表明，每年大约有接近15%的MCI患者转化成AD，而NC的转化率不到2%[2]。因此，尽早诊断MCI尤其重要。事实上，当下对MCI的诊断仍旧依赖于医生临床诊断经验和心理测量学评估，并且由于部分医生的主观性经验判断很容易造成MCI的误漏诊，导致病情耽误甚至恶化。因此辅助医疗诊断工具的研究与开发是十分必要的。

近几年，随着神经科学中脑连接组研究的不断深入，图论分析(graph theory analysis)的发展为脑神经疾病早期诊断的研究提供了重要的技术保证。研究者们发现依据功能磁共振影像(functional magnetic resonance imaging，fMRI)数据构建得到的脑网络不仅具有重要研究意义的拓扑特性，而且存在不同的功能模块组织，例如运动、默认网络、边缘系统、视觉、注意力处理等[3]。SPORNS et al[4]发现模块组织似乎在婴儿期就开始存在，并随着年龄的增长而退化，这表明它与认知能力有关。这为从模块化的角度解析拓扑特性提供了必要的理论基础。在之前模块化拓扑属性研究中发现，其连接不仅起着桥梁通信的作用，还能够更精确地反映各功能模块的信息交流规律和组织模式的变化。例如，AVENA et al[5]发现模块间和模块内连接的数量会随着年龄的变化而变化，并且连接的异常中断有可能会扰乱大脑结构本身。MEUNIER et al[6]研究发现模块间边连接模式的广泛改变反映了人类大脑结构变化。因此，基于模块化的连接特征较容易识别大脑结构的异常变化。

此外机器学习方法，如支持向量机(support vector machine，SVM)算法结合磁共振影像(magnetic resonance imaging，MRI)已广泛应用在MCI诊断中。例如，ERIC et al[7]使用偏最小二乘法分析原始MRI数据，利用SVM算法实现对NC和MCI分类。梁红等[8]选取功能脑网络中的异常属性作为特征进行了基于SVM的分类研究。崔会芳等[9]利用静息态fMRI数据构建有向功能连接矩阵，随后对提取到的脑网络拓扑属性进行方差分析，利用SVM学习模型对NC组和MCI组被试进行分类识别。然而在前期的研究中，传统的特征分析集中于脑区节点的拓扑属性，从连接数的角度分析脑连接损失的研究较少，且对节点属性进行研究时，许多研究只对提取到的多脑区节点特征进行了简单地合并，也未充分发挥功能模块对脑网络分析的优势。总体来说，未能实现更深层次对各脑区间交互信息和功能连接关联研究的目的。

本文首先基于模块化拓扑连接的新角度，首次提取桥梁连接数作为特征，与传统提取的脑网络特征相比，精确直观地反映出各功能脑区连接的异常损失，实现更深层次对功能模块交互作用与脑结构异常改变相关研究的目的。其次本文提取特征时，通过计算边的介数中心性选取桥梁连接，简化网络中冗余的功能连接，在保留网络的生理学意义的同时，可以更全面可靠地分析和理解脑部疾病的病理生理机制。最后，分类结果显示，基于模块化的桥梁连接数特征极大提高了MCI检测的正确率。

1 研究对象

本实验fMRI数据取自ADNI(alzheimer’s dis-ease neuroimaging initiative)数据集，此公开数据集利用AD的医学成像数据对其病理机制进行分析研究，得到研究者的广泛使用。实验包括79例NC被试以及56例MCI被试。被试的年龄、性别信息如表1所示。对两组被试施以单因素方差分析，结果发现在NC组与MCI组患者性别上没有显著差异，而在年龄上存在显著的差异。

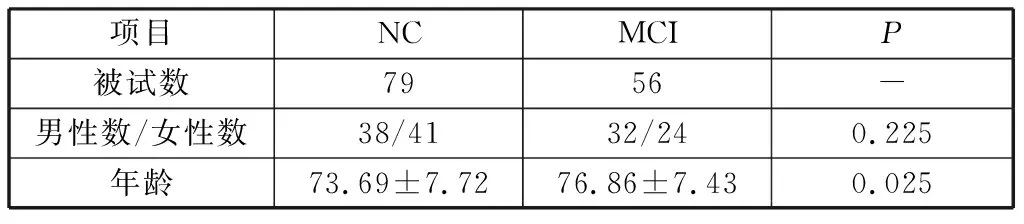
表1 被试性别及年龄信息Table 1 Information of gender and age of subjects

2 研究方法

2.1 数据采集及预处理

所有受试者闭上眼睛在3.0 T扫描仪(飞利浦医疗系统)上处于休息状态下完成的fMRI扫描。使用以下参数:重复时间(TR)为3 000 ms；回波时间(TE)为30 ms；皮层厚度为3.3 mm；皮层数为48；140个时间点。

本实验预处理基于Data Processing Assistant for Resting-state fMRI(DPARSFv2.3)工具[10]。针对每例数据的预处理流程：1) 首先将前10 s的功能图像丢弃；2) 对图像施以时间片校正和转动头动校正，只保留水平头动距离小于1 mm或者转动幅度小于1°的被试；3) 选择平面回波成像(echo planar imaging，EPI)中体素为3 mm的MNI标准空间模板对图像进行配准；4) 在进行过高斯平滑之后，选择0.01～0.1 Hz的低频滤波对图像数据中的低频漂移过滤及高频的生物噪音降低。

2.2 功能脑网络构建

在本研究中，通过计算得到时间序列之间的同步性，表达出功能关系在大脑区域间的异同。首先，利用解剖自动化的标记模板(automated anatomical labeling，AAL)[11]，对预处理完成后的功能图像划分成90个大脑区域，其中左右半球各45个脑区。功能脑网络中由单个节点代表对应的单个脑区。平均所有脑区内所包含体素的时间序列。然后通过使用多元线性回归分析的方法去除由头动带来的可避免脑信号误差影响。最后基于每对脑区间得到的平均时间序列计算皮尔逊相关，由此构建相关矩阵(90×90)。为了对脑网络实现后续的模块化及应用研究，基于NC组被试功能矩阵中各脑区的相关系数计算其算术平均值，得到NC组均值相关矩阵(90×90)如图1(a)所示。研究中，采用稀疏度S来进行阈值设置，目的是生成一个二值连接矩阵A，并根据图论分析脑功能连接网络的属性。本研究设定阈值S为15%构建出被试的脑功能网络，这不仅能够保证脑网络基本特性存在，也能最大程度地去除伪连接。NC组稀疏后的脑网络如图1(b)所示。

图1 79例NC组所构建的平均脑网络Fig.1 Mean correlation matrix constructed of 79 NC groups

2.3 模块度

自模块度(modularity)定义由Newman和Girvan提出后，越来越多的研究将其选作模块化算法的衡量依据[12]。模块度指标Q量化了实际网络中模块内连接数与随机网络中连接数之间的差异，简而言之，模块内和模块间连接的关系决定了每个模块的强度[13]。在本次研究中，应用“堆结构”的贪婪算法，实现寻找全局最优模块度M及划分模块，在脑网络中的每个节点都代表一个独立的社区。之后，社区被反复合并成越来越大的成对，在每个步骤中选择合并，以使Q最大增加或最小减少(如果不再可能增加)。模块度定义为：

(1)

式中：NM代表模块化后的所有模块总数，L代表当前网络中所有边的条数，LS表示模块S内包含的节点间连接的条数，dS表示在模块S内所有节点度的总和。如图2所示，在模块及边连接示意图中，由红色、黄色、蓝色节点分别组成3个独立的模块，同一模块内包含的边与节点颜色一致，模块间连接的颜色为灰色。

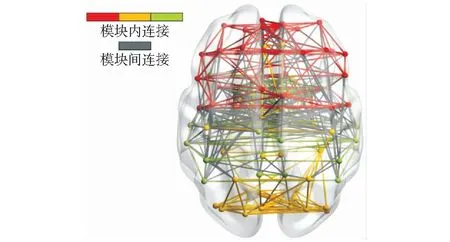
图2 模块及连接示意图Fig.2 Schematic diagram of modules and connections

2.4 全局桥梁连接

为了确定每条连接在功能脑网络中信息交流的重要性，我们计算了每条连接的介数中心性[14]，连接介数中心性定义为：

(2)

式中：σst表示从节点s到节点t距离最短的路径条数，σst({i,j})表示从节点s到节点t且之间经过特定连接(节点i与节点j之间的连接)的距离最短的路径条数。

2.5 特征提取及统计分析

提取特征第一步：使用基于“堆结构”的贪婪算法对NC组(90×90)平均相关矩阵进行模块划分(为忽略MCI组和NC组的个体模块差异，MCI组使用NC组的模块划分结果)；第二步：通过图论计算NC组与MCI组功能连接矩阵中每条连接的介数中心性，筛选全局桥梁连接，关于桥梁连接提取的方法，已在2.4节中详细阐述；第三步：计算各模块间与模块内全局桥梁连接数。

本研究使用SPSS19，单因素方差分析判断NC、MCI的模块内及模块间桥梁连接数是否存在显著组间差异，并去除性别、年龄协变量对检验结果的影响。

2.6 分类模型构建

SVM分类器由SUYKENS et al[15]基于结构风险最小化原理提出的一种机器学习算法，其特点是具有较强的泛化能力且涉及的参数较少，因此比较适合对小样本数据进行分类。使用SVM分类器时，有多个核函数可供选择，因研究基于不稳定的脑影像信号进行分类，选择SVM径向基核函数(radial basis function，RBF)映射特征空间。其中，涉及到C和g两个参数。C是惩罚因子，g是核参数。为了获得更好的分类效果，设置C和g的范围为[2～8,28]，步长1，随后通过网格搜索的方法，可取得最优的(C,g).

为实现对疾病数据建模及自动识别，利用机器学习方法，选择SVM(RBF核函数)算法，使用交叉验证随机选择所有样本中的70%为训练集，剩余30%为测试集，重复100次。生成并评测模型来计算平均正确率、特异率、敏感率。

3 结果与分析

3.1 模块化

利用“堆结构”贪婪算法实现对正常组的脑网络的模块划分，得到如图3所示的5个模块并由5种颜色分别表示。表2为各模块(标记为M1至M5)中所包含节点信息。

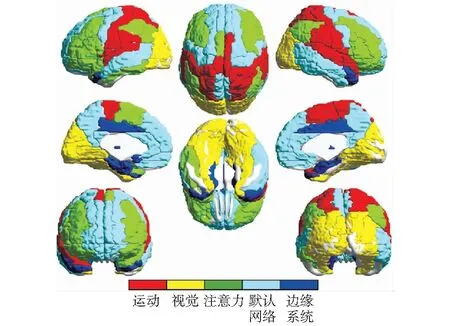
图3 模块划分结果图Fig.3 Graph of modular division result

表2 模块划分结果Table 2 Result of modular division

综合模块划分结果来看，M1的脑区主要来自(前)运动皮层、顶叶和颞叶皮层的区域，这些区域主要与躯体感觉、运动有关[5]。M2的脑区主要分布于枕叶，其主要功能包括：动作、语言、抽象概念及视觉处理等[16]。M3的脑区主要参与注意力处理，其主要功能包括：自我意识、记忆、意识与知觉[17]。M4的这些区域是额叶内侧和颞中回的关键组成部分，属于RALCHLE et al[18]描述的“默认”网络。M5的脑区属于边缘系统，其主要功能包括：产生情绪、学习记忆等[19]。这与先前研究划分模块的结果较为一致。

3.2 统计分析

在统计分析中，图4是Bonferroni校正后两两比较模块内及模块间桥梁数的具体信息(图中横坐标表示各模块内、模块间)。

由图4可知，在MCI患者的功能脑网络中，并非只出现少数功能模块间及模块内的桥梁连接缺失，而是在多个功能模块间及模块内均发现存在着不同程度的桥梁连接损伤及补偿。在前人的研究当中，JI et al[20]基于正常老年人的功能和结构磁共振成像数据，通过空间独立分量分析(ICA)发现，当核心脑区中灰质(GM)结构体积逐渐变小，需要激活网络连接数量增多(r=0.408，p=0.035)，视觉、注意力会出现补偿机制，即会增加网络之间的连接。SHENG et al[21]发现MCI在内侧颞叶的记忆脑区结构会明显萎缩同时发生连接补偿，更指明内侧颞叶功能连接的增强有助于鉴别AD倾向受试者，这与本研究发现基本一致。

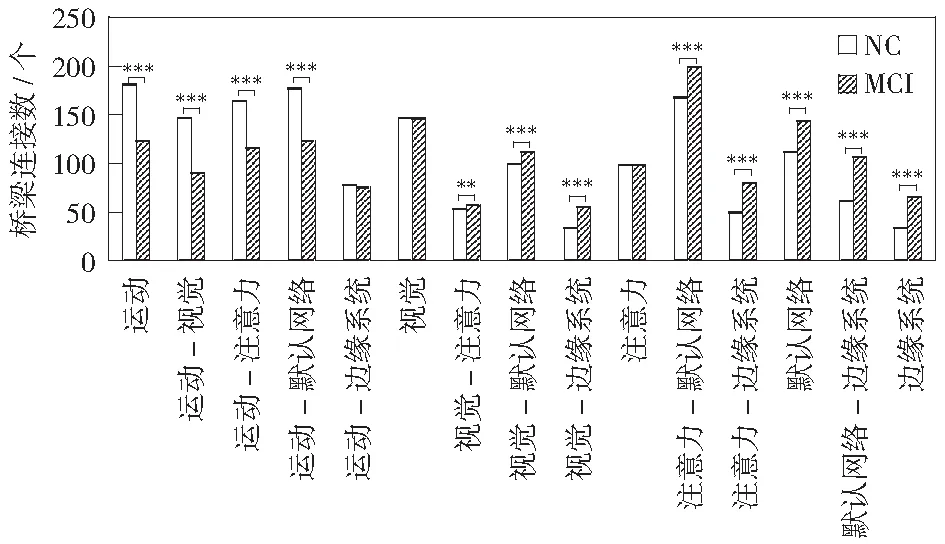
图4 模块内、模块间边连接数的差异Fig.4 Difference in the number of global edges in within-module and between-module

3.3 SVM分类

本研究将桥梁连接数作为输入特征，利用7折交叉验证方法对NC与MCI进行分类，平均分类正确率达到92.89%，平均特异率为94.29%(健康人中得出阴性检测的样本占健康人总数的百分比)，平均敏感率为97.14%(病人中得出阳性检测的样本占病人总数的百分比)。因此，从分类正确率来看，本研究发挥出了模块化桥梁连接数对脑网络分析的优势，证明了本特征选择方法的有效性。

对比先前基于fMRI提取脑网络特征方法的研究，本文应用于特征提取的方法明显提高了分类正确率。梁红等[8]将功能脑网络中的异常属性输入SVM训练学习模型中作为特征对NC、MCI分类，得到正确率为75.33%。接标等[22]利用fMRI数据，构建网络得到局部节点多层次拓扑特征对MCI和NC分类，正确率为82.6%。郭浩等[23]基于fMRI数据构建脑网络，利用得到的模块内网络属性度与参与系数对NC与抑郁症病人进行分类，最高正确率达90.5%。这些都说明在当前的研究中利用节点拓扑属性作为特征进行疾病诊断及分类必然会使得信息分析不够全面充分，进而对研究的分类性能造成影响。因此现将脑网络拓扑连接边应用在分类研究的方法已经被越来越多的研究认可。另外，从模块的角度对脑网络桥梁连接进行研究，更能有效直观地发现脑部疾病患者与正常人在大脑功能模块上的差异，提高分类正确率。

4 结束语

图论作为研究复杂系统的基础与工具，成为脑精神疾病分类研究的热点。但是，已有的基于图论提取功能特征的方法较为繁琐且单一，无法直观有效地衡量脑结构的改变带给功能模块间信息交流组织模式的影响。为了解决这些问题，本研究首先基于脑网络模块化的角度，选取桥梁连接数作为样本特征对MCI和NC进行分类，精确直观地反映出模块连接组织模式变换与脑结构改变的相关程度。其次，本研究在不影响脑网络生理学意义的前提下，筛选桥梁连接去除了冗余的功能连接，与之前脑网络特征选取方法等相比，该方法概念简单，运算量小，因而计算复杂度大大降低，运算速度提高，实现利用最少的特征数达到最高的分类正确率的目的。最后，分类结果显示，基于模块化提取桥梁连接数特征的方法大大提高了MCI检测的正确率，从而更好地辅助MCI的诊断，以便及早发现病情。