考虑土壤水平衡的灌区水资源优化配置研究

赵 敏 郭 萍 张 妍

(中国农业大学 水利与土木工程学院，北京 100083)

河套灌区是我国3 个特大型灌区之一，平坦的地势以及便利的引黄灌溉条件使其成为重要的商品粮基地和产油基地。解放闸灌域(106°43′～107°27′E,40°34′～41°14′N)是河套灌区第二大灌域，引黄灌区面积占总种植面积的95%，农业用水几乎全部依赖于引黄灌溉，是典型的无灌溉则无农业的地区[1]。但长年的引黄漫灌不仅导致灌溉效率低下，而且引发地下水矿化度高、土壤盐渍化等问题。这些因素严重影响当地农作物正常生长，制约了农作物产量提高[2]。近年来黄河受到气候变化与人类活动影响，径流量逐年减少，城镇化进程不断加快，建设用水量大幅度增加，农业灌溉用水供需矛盾不断加剧[3]。因此，迫切需要借助灌区水资源优化配置技术对有限农业水资源进行优化分配，提高水资源利用效率。

灌区水资源优化配置被证明是实现灌区高效用水的有效方法,即：在整个灌溉季节，将灌区可利用的、有限的水资源在时、空上进行合理的分配，获得全灌区最高的产量或收益[4]。该技术在我国黑河、石羊河流域及东北地区已得到较好应用，为当地农业水资源配置规划提供了决策参考。早期优化配水模型一般基于相对简单的线性规划模型结构进行构建，以达到整个灌区净经济效益最大的优化目标[5]。随着Jensen模型的引入，水资源优化配置模型在农业水资源管理应用方面进一步发展，可以通过优化方法得到不同作物的灌溉制度[6]。已有研究在进行水资源优化配置研究时，越来越注重如多目标、区间、模糊等优化方法的拓展与选择，却一定程度上忽略了优化模型对于具体问题中一些特殊环境的适用性。对于河套灌区地下水埋深较浅，土壤水与地下水交换频繁的特殊水文环境，相关优化模型适用性还有待提高[7]。已有研究也会忽略作物对不同时期土壤水分和农业水循环的响应以及灌溉系统的水文循环过程，不考虑地下水潜水蒸发对土壤含水量带来的影响[8-9]。而将水资源优化配置模型与土壤水平衡模型相结合是解决以上问题行之有效的改进方法[10]。2017年，Li等[10]综合考虑到内蒙古河套灌区地下水埋深较浅的情况，以玉米这种植面积大的高耗水作物作为典型作物，将作物水模型和水循环模型与不确定性优化模型相结合进行优化配水，在实现较高的经济效益基础上获得了玉米的灌溉制度。但是，上述研究尺度为田间尺度，而在实际灌溉水资源管理中对于水资源的调配是在整个灌区或区域进行的；相关试验研究表明，初始地下水埋深及土壤含水量对土壤水与地下水转化有较明显的影响，间接影响了灌溉水量的配置[11]。因此，在考虑初始地下水埋深及土壤含水量条件下，从灌域尺度来研究解放闸灌域玉米灌溉制度优化方案对于实际水资源策略制定有一定指导意义。本研究为优化分配有限引黄灌溉水量以实现灌区最大的净经济效益，拟采用将水分生产函数模型、土壤水平衡模型与水资源优化配置模型相结合的研究方法，在灌域尺度上构建考虑土壤水平衡的水资源优化配置模型，对河套灌区解放闸灌域玉米灌溉水资源优化配置问题进行研究，以期为灌区管理者提供多情景下合理的优化配水方案，助力灌区可持续发展。

1 材料与方法

1.1 模型建立

1.1.1模型基本框架

针对解放闸灌域农业用水供需失衡、地下水埋深浅等问题，本研究构建了基于土壤水平衡的水资源优化配置模型来分配引黄灌溉水量，模型基本框架图如图1所示。模型通过实际蒸散量这一参数建立Jensen水分生产函数模型，土壤水平衡模型及优化配水模型三者之间的相关关系。模型以天为基本时间步长，以月作为配水时间尺度，灌水量作为优化模型决策变量，作物产量作为输出变量，通过优化模型最大化经济效益，确定多情景下的优化配水方案。

1.1.2Jensen模型

非充分灌溉条件下，作物灌溉配水研究通常需要借助水分生产函数来反映作物各生育阶段水分亏缺对作物产量影响。本研究选用的是Jensen连乘动态模型[12]，其表达式为：

(1)

式中：i为作物生育阶段编号；n为作物生育阶段数；ETai为第i个生育阶段作物实际蒸腾量，mm；ETmi为第i个生育阶段作物最大蒸腾量，mm；Ya为作物在实际蒸腾量下对应的实际产量，kg/hm2；Ym为作物在最大蒸腾量下对应的最高产量，kg/hm2；λi为第i个生育阶段作物水分敏感指数。

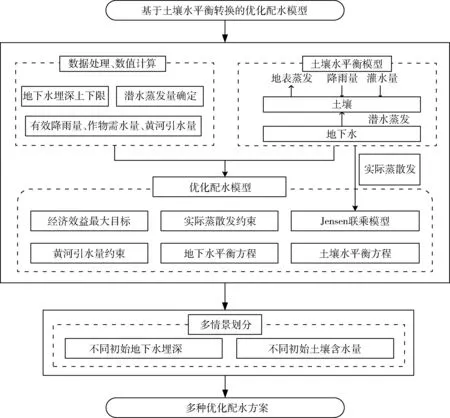
图1 模型研究框架图Fig.1 The study framework of the model

采用Jensen模型是利用生育期ET计算作物产量，一般通过田间试验得到不同生育期的水分敏感指数。在本研究中，采用1 个月作为模型的阶段。因此，生长阶段的水分敏感指数需要进行回归转化[14]：

(2)

式中：t为播种后的天数，通过累积函数Z(t)，从ti-1到ti时刻，水的敏感性指数可以用以下公式计算：

λi=Z(ti)-Z(ti-1)

(3)

Wang等[15]用logistic曲线描述了水分敏感指数随时间累积值的变化如下：

(4)

式中：K、b、m为经验系数。

1.1.3土壤水平衡模型

由于解放闸灌域的地下水埋深浅，作物对不同时期土壤水分和农业水循环的响应不可忽略。通过查阅相关论文及数据资料，解放闸灌域主要土壤类型为砂壤土，土壤种类变化不大，因而本研究假设农业生产的下垫面是均质土壤并且土壤含水量一致。作物实际蒸散发(ETai)处于不断变化之中，可通过土壤水平衡公式进行估算。土壤水分平衡考虑主要成分包括灌溉(IW)，降水(P)，地下水蒸发(ETg)，实际蒸散发(ET)。如果研究区域降雨少，地形相对平坦，地表径流径流量小，地表径流常被忽略不计[10]。土壤水平衡的时间步长为1 d，作物土壤水分平衡方程可表示为：

ΔWi=n×(θi+1-θi)

(5)

ΔWi=IWi+Pi+ETgi-ETai

(6)

(7)

式中：ΔWi为第i天土壤含水量变化值，mm；n表示地下水埋深，1 m；θi，θi+1分别表示第i天和第i+1天土壤含水量，本研究中的土壤水含量为0.08～0.20[10]；IWi表示第i天灌水量，mm；Pi表示第i天的有效降雨量，mm；ETgi为潜水蒸发量，mm；ETai为第i天实际蒸散发量，mm；Qt为第t月的灌水量，m3；η为灌溉水利用系数；A表示研究区域灌溉面积，hm2。

地下水蒸发是将浅层地下水转化为土壤水和大气水的重要途径，也是地下水的主要消耗。本研究用Hu等[16]提出的计算地下水蒸发的经验公式，该模型在新疆得到了高精度模拟结果。

ETgi=2.954 7×(hi)-1.762 9×
(1-e-(0.087 7×hi-0.011 2)×Ei)

(8)

式中：Ei为蒸发皿蒸发量，mm；h为地下水埋深，m。

作物生长过程中的潜水深度由每天的地下水平衡方程(9)计算。对于浅层地下水，地下水与土壤水的交换十分频繁。地下水消耗主要包括农田潜水蒸发和侧向排泄，本研究中忽略侧向排泄，在水量平衡的基础上，研究地下水动态变化关系。

1 000μ(hi-hi+1)=-ETgi

(9)

式中：hi，hi+1分别表示第i天和第i+1天地下水埋深，m，解放闸灌域的地下水埋深约为1.0～3.8 m[10]；ETgi为第i天的潜水蒸发量，mm；μ为特定的饱和土壤含水量，70 mm/m[10]。

1.2 案例研究

1.2.1水资源优化配置模型构建

本模型以净经济效益最大为目标，以月灌溉水量为决策变量，并在实际蒸散发和黄河可供水量的约束下，结合Jensen模型和土壤水平衡模型建立优化配水模型，利用Lingo软件进行求解，输出各生育期灌水量、日实际蒸散发量、潜水蒸发量、土壤含水量、地下水埋深、系统净经济效益等值。

(10)

优化配水模型应设置约束条件：

1)实际作物蒸散发约束：

ETt≤ETmaxt

(11)

(12)

(13)

2)土壤水平衡约束：

θi+1=θi+IWi+Pi+ETgi-ETi

(14)

3)黄河可供水量约束：

黄河在作物生长期内的供水量作为一个刚性水量指标可以用于灌溉，但不能超过最大供水量Qγ。研究区域以黄河为水源，在作物生长阶段，每年约3.85×108m3。

(15)

4)非负约束：

Qt≥0,∀t

(16)

式中：F为种植净效益，元；i为不同天数；t为不同月份；B为玉米单价，元/kg；灌溉面积，hm2；TC为种植成本，元/hm2；S为用水成本，元；A为灌溉面积，hm2；Qt为不同时段供水量，m3；Ymax作物最大产量，kg/hm2；ETt为第t月作物的实际蒸散发量，mm；ETmaxt为第t月最大蒸散发量，mm；ETai为第i天实际蒸散发量， mm；ETmi为第i天最大蒸散发量，mm；θi+1为第i+1 天土壤含水量；θi为第i天土壤含水量；IWi为第i天灌水量，mm；Pi为第i天有效降雨量，mm；ETgi为第i天潜水蒸发量，mm。

1.2.2基础数据

解放闸灌域属于显著的大陆性气候，降雨量小而蒸发量大，年平均降水量为140 mm，蒸发量约为2 000 mm。据历年《引黄灌区成果报告》显示，该灌域总灌溉面积为14.209万hm2，其中引黄面积约占总灌溉面积90%以上，本研究采用平水年的年均引黄水量，约12亿m3。灌溉水的成本一般与种植时间有关，4—9月水价为0.083元/m3[10]。灌溉作物包括主要作物(玉米、小麦、向日葵)和蔬菜、甜瓜等，本研究选择种植面积最大的玉米(约占总种植面积的35%)作为典型作物，种植面积约32 047 hm2，每年玉米灌溉用水量约3.85×108m3。根据《巴彦淖尔市统计年鉴2017》[13]，玉米价格为2.4 元/kg，用于作物种植花费的成本为每公顷10 500元。参考Li等[10]计算结果以及气象站获得的临河气象资料得出玉米不同月份ETmi和λi如表1所示，且玉米最高产量为12 850 kg/hm2。

本研究的作物需水量采用作物系数法确定，其中参考作物蒸发蒸腾量ET0采用Penman-Monteith公式计算[18]，解放闸灌域生育期内各月份ET0值如表2所示。本研究选用Chen等[19]确定的蒸发皿系数0.53，作物蒸发蒸腾量及蒸发皿蒸散发量计算如下：

ETc=KcET0

(17)

E=ET0/0.53

(18)

式中：ETc为作物蒸发蒸腾量估计值, mm；Kc为作物系数；ET0为参考作物蒸发蒸腾量, mm；E为蒸发皿蒸发量, mm。

3 结果与分析

利用Lingo软件对上述综合优化模型进行求解，并将日最大蒸散发量、日有效降雨量、可供水量及社会经济等数据输入基于土壤水平衡的水资源优化配置模型中，输出决策变量(实际蒸散发量ETa、灌水量IW)以及通过模型公式计算得出的潜水蒸发量ETgi、地下水埋深Hi和土壤含水量θi等参数，观察其每日变化情况。内蒙古河套灌区解放闸灌域地下水埋深较浅，潜水蒸发量较大，地下水埋深(为1～4 m)和土壤含水量(为0.08～0.20)对灌水量和模型结果有较大的影响，并且有关研究表明，研究区域地下水埋深及土壤含水量存在时空变化特征[21]。因此，本研究将先以初始土壤水含量为固定值，划分7 种不同的地下水埋深情景，并综合考虑灌区实际情况，选定其中一种初始地下水埋深情况，进一步进行 7种不同初始土壤含水量情景划分。

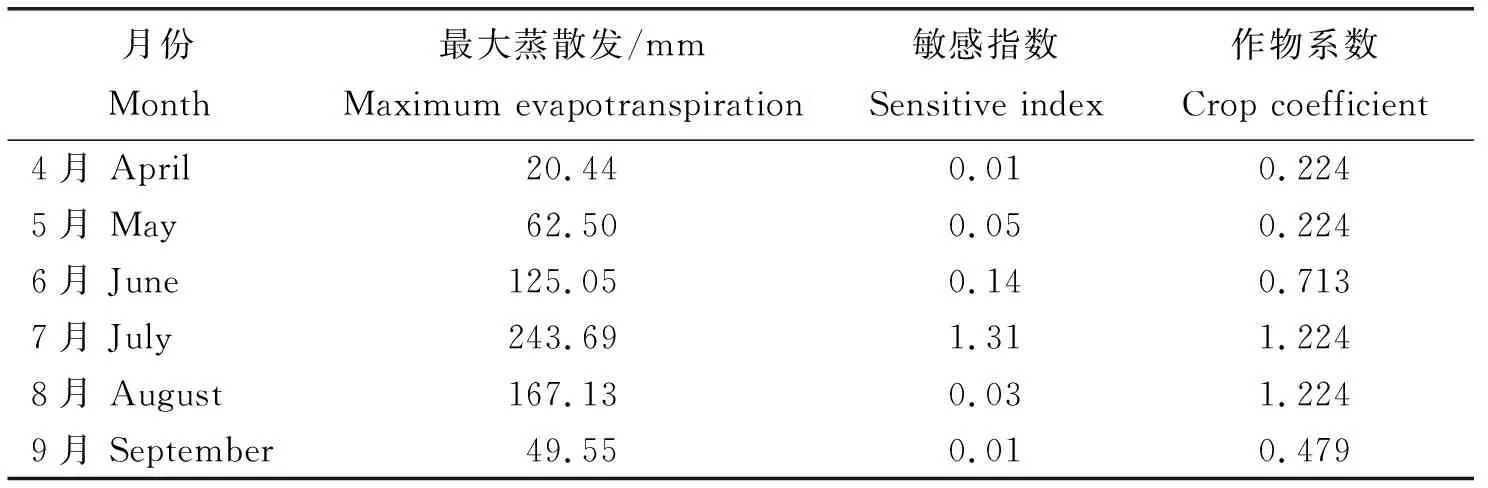
表1 解放闸灌域玉米各月份相关参数Table 1 Related parameters of maize in Jiefangzha irrigation area

表2 解放闸灌域各月份参考作物蒸发蒸腾量ET0值Table 2 Monthly refercence crop evapotranspiration ET0 Jiefangzha irrigation area mm

3.1 不同初始地下水埋深对优化结果的影响

解放闸灌域地下水埋深处于1～4 m，因而将初始地下水埋深划分为7 种不同情景(1.0、1.5、2.0、2.5、3.0、3.5、4.0 m)，探究不同生育期的潜水蒸发量、不同生育期总灌水量、系统净经济效益及地下水埋深变化值随初始地下水埋深变化情况。

图2为潜水蒸发量与地下水埋深变化量随初始地下水埋深变化规律。由图2可以看出，随着初始地下水埋深的增大，潜水蒸发量逐渐减少，在地下水埋深为1 m时潜水蒸发量甚至达到了地下水埋深为4 m时3倍之多，可见初始地下水埋深对灌溉过程中的潜水蒸发具有显著影响。此外，随着初始地下水埋深增大，地下水埋深变化量也逐渐减小。当初始地下水埋深为2.5 m时，地下水埋深变化量曲线出现了拐点；当初始地下水埋深小于2.5 m时，地下水埋深变化量较大且斜率较大；地下水埋深大于2.5 m时地下水埋深变化量小且斜率降低。

为探究初始地下水埋深对灌溉水量的影响，对不同情景下春玉米各个生育阶段灌溉水量分别求解，其优化结果见图3。结果表明灌溉总水量均小于作物需水量。灌水量主要集中在6、7、8月份，并且除了地下水埋深为4 m时的情况，灌水量最大值均出现在7月份，最小值出现在9月份。灌水量最小时引黄水量为0 m3，作物生长所需水量全都由降雨提供。该优化结果与作物耗水量分布一致，符合实际情况。

当初始地下水埋深浅时，灌水量都小于需水量；而当初始地下水埋深大于2.5 m时，出现部分灌溉水大于需水量的情况。这是因为初始地下水埋深浅，部分地下水可通过潜水蒸发补给土壤水用于作物生长；而当初始地下水埋深大时，潜水蒸发量小，部分引黄水量下渗补给地下水。

作物全生育期灌水量随地下水埋深变化的关系如图4 所示。研究发现初始地下水埋深对作物灌水量大小及各生育期分布均有一定影响，随着初始地下水埋深的增大，引黄灌溉水量也不断增大。与此同时，根据净经济效益可知，农业经济效益随地下水埋深增大不断降低：当初始地下水埋深为4 m时，系统产生的净经济效益为5.49×108元；当初始地下水埋深为1 m时，系统产生的净经济效益为5.67×108元。不同情境系统产生的净经济效益在5.49×108～5.67×108元。将优化结果与作物需水量结果进行比较，结果发现当地下水埋深为2.5 m时，当地可节约引黄水量约5.34×107m3，净经济效益达到5.55×108元。

3.2 不同初始土壤水含量对优化结果的影响

综合上述结果及实际情况，本研究选取地下水埋深为2.5 m的情景，进行不同初始土壤水含量情景划分。初始土壤含水量情景划分为0.080、0.100、0.120、0.140、0.160、0.180、0.193这7种，并探究其对净经济效益、灌水量、潜水蒸发量、实际蒸散发量，地下水埋深变化值等要素的影响。

在不同初始土壤含水量情景下(图5)，分析灌水量在各生育期分配情况。优化结果表明土壤含水量不断变化时，各生育期灌水量也在不断变化之中。当土壤含水量较低时，应当在4、5月份灌溉一定水量以满足作物对土壤水分的需求；而随着土壤含水量的增加，灌水量不断向7、8月份集中，在这两个生育阶段作物生长所消耗的水分较大。输出结果与实际情况相对应。

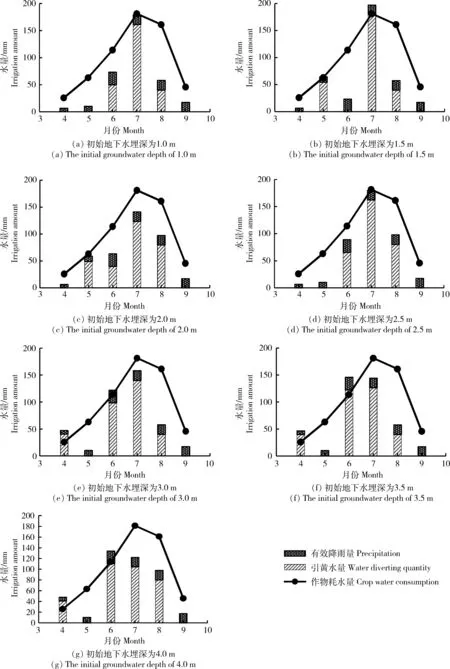
图3 不同地下水埋深情景下灌水量在各生育阶段分配情况Fig.3 Irrigation water distribution of different growth stages under different groundwater depth scenarios

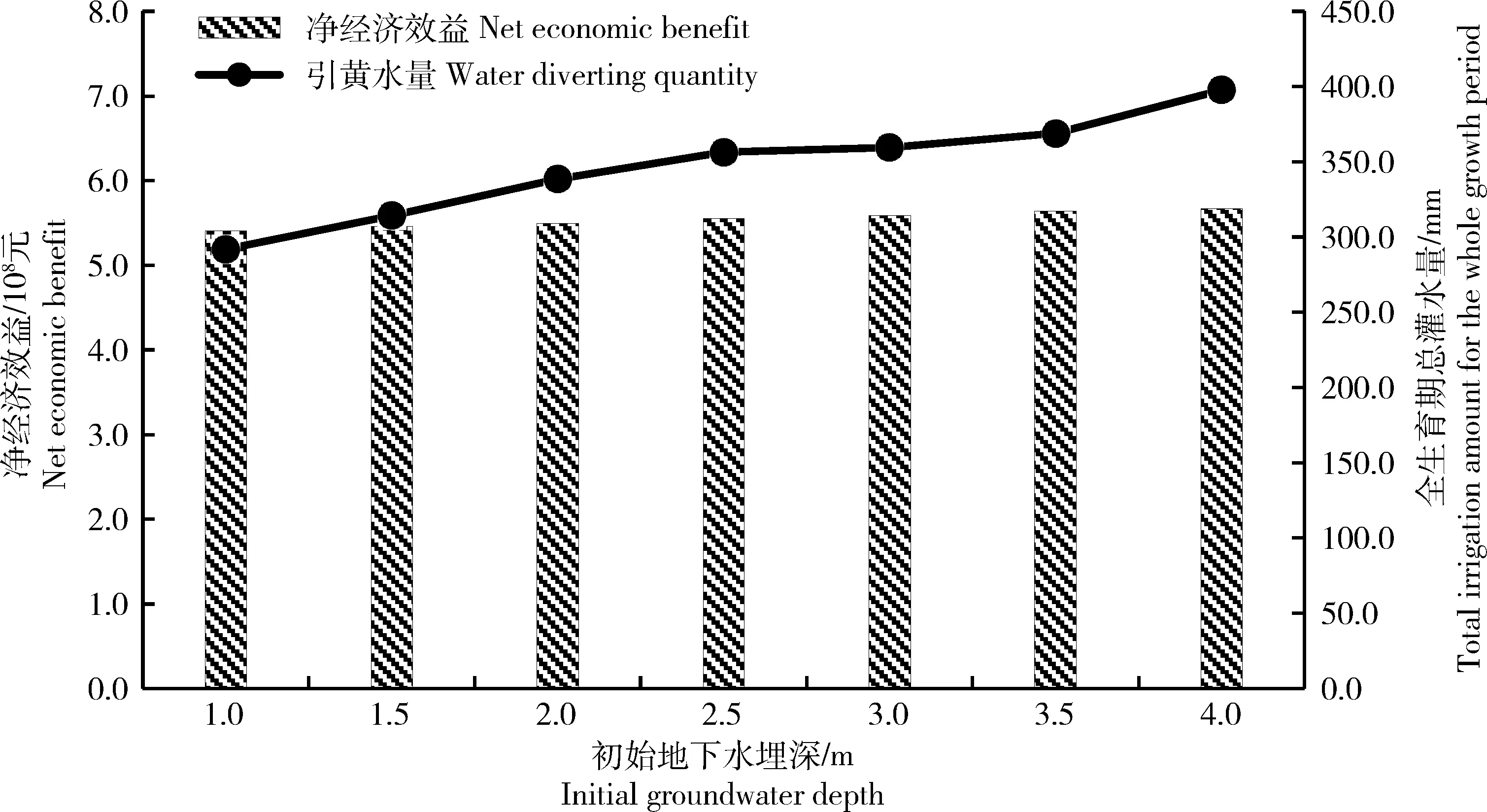
图4 系统净效益及全生育期灌水量随不同初始地下水埋深的变化情况Fig.4 The net economic benefit and total irrigation water amount with different initial groundwater depth

为了进一步了解作物全生育期灌水量及系统净经济效益受初始土壤含水量影响，建立作物全生育期灌水量及系统净效益与初始土壤含水量变化的关系(图6)。土壤含水量对作物灌水量大小及各生育期的分布均有一定的影响。随着初始土壤含水量增大，引黄灌溉水量也不断减小。此外，随着初始地下水埋深增大，农业经济效益呈现先增大后减小的趋势。当初始土壤含水量为0.080时，系统净经济效益为5.41×108元，当初始土壤含水量为0.193时，系统净经济效益为5.67×108元。多种情境下系统净经济效益约为[5.41,5.67]×108元。研究结果表明，当土壤含水量控制在0.12～0.16时，运用该配水方案可以提高水资源利用效率。

综合上述分析结果可知，初始地下水埋深及初始土壤含水量对引黄灌溉水量及系统净经济效益有较大的影响。研究表明[22]地下水埋深2.5 m可作为土壤轻度盐渍化的一个临界值，即当地下水埋深小于2.5 m时，产生土壤盐渍化问题。地下水埋深变化量过大或者过小都不好，地下水埋深变化在一定范围内就可以保证作物正常生长并避免土壤盐渍化。张义强等[23]、杨会峰等[24]通过在解放闸灌域进行实验研究发现，在大部分地区，地下水埋深2.5 m是轻度盐渍化的临界点，当地下水埋深小于2.5 m时，出现轻度盐渍化现象。而地下水埋深控制在2.0～2.8 m较合适，可保证作物的正常生长并缓解土壤盐渍化的问题。本研究结果与上述研究一致，表明模型在当地具有一定的适用性。

4 讨 论

针对河套地区地下水埋深浅、土壤盐碱化的问题，已有相关研究[25]考虑了地下水位、土壤含水量，进而获得灌溉水量配置。本研究是对Li等[10]所发展方法的改进，本研究选取初始地下水埋深为2.5 m，初始土壤含水量为0.14情景下的作物需水量、引黄水量、净经济效益值与Li等[10]的水量分配研究结果进行对比。2 种方法所获得各月份作物需水量与引黄灌溉水量对比情况如表3所示。本研究得到的各月份作物需水量值和引黄灌溉水量均相对偏少，但是相差不大，表明将模型从田间尺度运用到灌区尺度有一定的可行性。有研究表明当灌水量超过作物需水量时，作物的产量不会增加反而降低。在Li等[10]的研究中，5月份的灌水量值超过了作物需水量，造成了水资源的浪费，而本研究的所有情景都满足灌水量小于作物需水量这一条件的(表3)，其优化后的配水结果约为4 526 m3/hm2，并产生1.53×104元/hm2的经济效益；本研究优化后引黄水量约为4 145 m3/hm2，产生1.64×104元/hm2的净经济效益。即在初始地下水埋深及土壤含水量较合适的情景下，每hm2可节约灌溉用水381 m3，并增加1 100元经济效益。因此，通过本研究的方法所获得得到的优化结果有更高的单方水效益，用水效率更高。

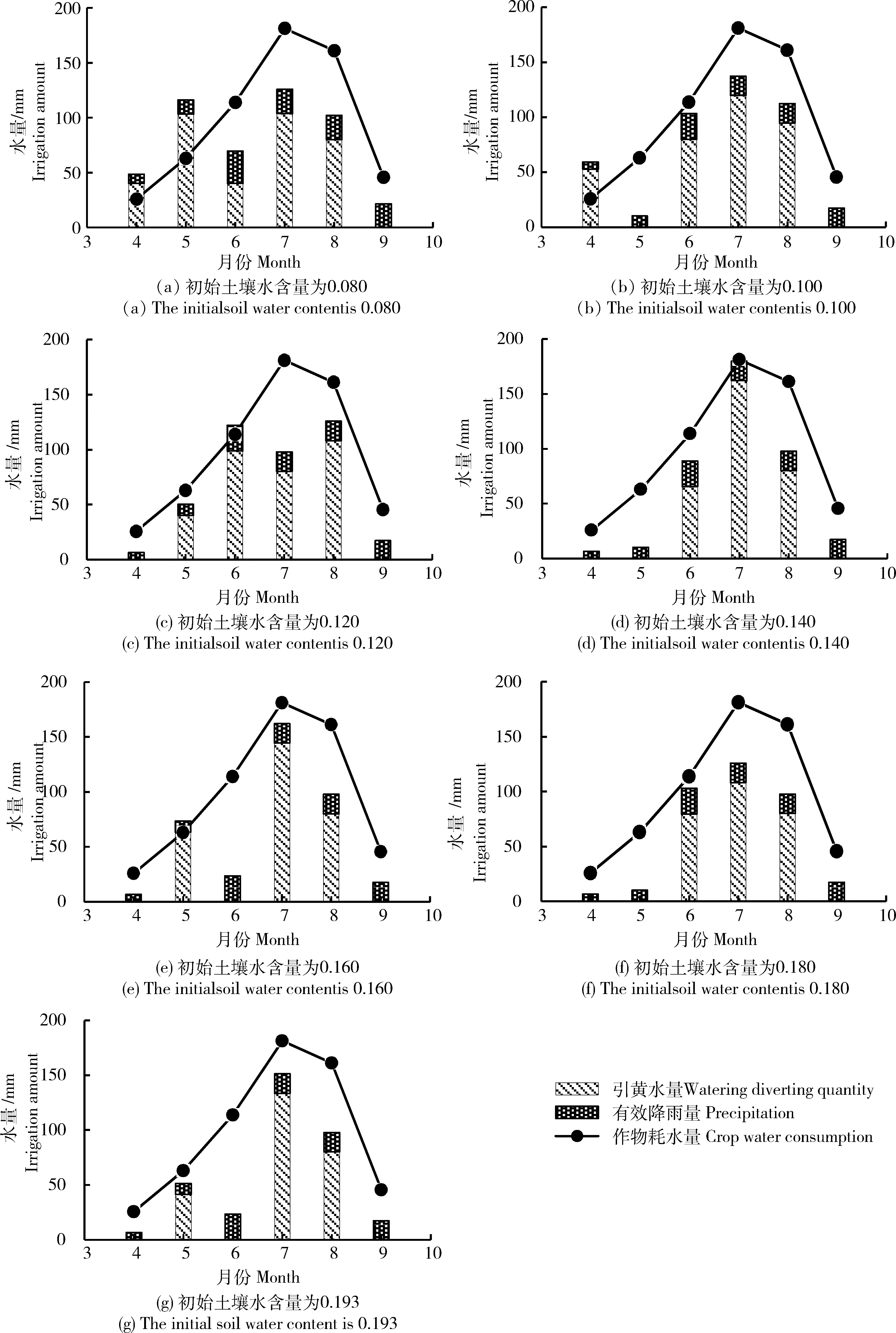
图5 不同土壤水含量情景下灌水量在各生育阶段的分配Fig.5 Irrigation water distribution of different growth stages under different soil water content scenarios

图6 全生育期引黄水量及系统净经济效益随不同初始土壤含水量的变化Fig.6 The net economic benefit and total water diverting quantity with different initial soil water content

表3 解放闸灌域玉米各月份作物需水量与灌溉水量对比值Table 3 The comparison value of crop water demand and irrigation waterdemand in each month in the irrigation area of Jiefangzha area

灌区内的灌溉水资源配置通常需要同时考虑多种作物，但由于资料所限，本研究只针对解放闸灌域的玉米进行研究，今后将尝试收集更多基础数据，以本研究所构建模型为框架，同时对更多作物进行优化配水研究。此外，本研究对于不确定性信息的考虑较少，未来研究中将尝试对配置系统中的不确定性信息进行描述与表征，并引入不确定性方法进一步丰富模型，使研究结果更具实际意义。

5 结 论

本研究构建了基于土壤水平衡的水资源优化配置模型并将其应用于河套灌区解放闸灌域，得到了14 种情景下的优化配水方案。结果表明，初始地下水埋深越浅，所需引黄灌溉水量越少，系统净经济效益越大；初始土壤含水量越小，引黄灌溉水量越大，得到的系统净经济效益越小。此外，当地下水埋深为2.0～2.5 m，土壤含水量为0.12～0.16时得到的配水方案较优, 达到[5.50, 5.59]×108元净经济效益基础，节约引黄水量约5.34×107m3。本研究验证了模型在灌区尺度进行单一粮食作物水资源优化配置的可行性，将为类似地区解决有限水资源配置问题提供配置思路与模型基础。在实际的区域农业水资源配置中往往有多种作物，因此在未来的研究中将考虑基于本研究模型框架建立多作物优化配水模型来指导实际水资源配置。