基于改进流行排序算法的显著性区域检测
2020-07-21鲁文超段先华
张 静, 鲁文超, 段先华
(江苏科技大学 计算机学院,镇江 212003)
人的视觉注意机制可以准确、快速定位自然场景中最引人注意的物体或区域,计算机通过模仿这一视觉注意机制原理形成显著性检测技术,是图像处理中关键的一个阶段,广泛应用于目标识别[1-2]、视频压缩[3]、图像检索[4]、图像分类[5]等研究领域.
现有的显著性检测算法在检测存在一个或者两个显著目标和背景简单的图像时能够获得很好的结果,但是面对复杂背景或者存在多目标(两个及其以上)时,检测效果无法满足实际要求.因此文中提出一种基于改进流形排序算法的显著性区域检测算法,通过多特征计算上、下、左、右4个方向的显著图,解决了通过单一特征计算的结果不够精确的问题,通过超像素分割算法将图像分割成4个不同的尺度,分别计算4个尺度下的显著图.不同尺度下,分割图像的细节信息不同,图像分割的超像素数量过少的话,很多不属于同一特征属性会被分割在一起,不利于检测,分割的数量过度,会严重增加算法的时间复杂度,因此,通过实验综合考虑文中选择了4种尺度.现有基于图的流行排序的显著检测算法中通过阈值分割得到最终的结果,由于阈值选择存在一定缺陷,文中通过多核提升对检测的弱显著图进行进一步处理,得到更加精确的显著图.
计算机视觉领域的显著性检测方法通常包含两种:自顶向下[6-7](任务驱动)和自底向上[8](数据驱动).早期显著性检测模型的研究主要集中于人的视觉注意机制,最早的显著性检测模型由文献[10]受生物模型启发提出自底向上的显著性模型,文献[11]提出频率域的计算方法,通过计算图像在频率域的冗余部分和变化部分得到图像的显著图.文献[12]从频域角度出发,提出一种基于全局对比度的显著区域检测算法,该算法首先对输入图像进行高斯滤波,然后将滤波后的图像中的每个像素值和整幅图像的平均像素值之间的欧几里得空间距离作为该像素的显著值度量.频率域的计算模型简单易于实现并且计算效率高,但过分强调图像的边缘且频率域与空域之间的转换图像会丢失一部分信息,所以得到的显著图比较模糊.近年来,文献[13-14]通过图像底层和中层视觉信息结合贝叶斯理论,将显著性问题转换为概率计算问题.基于贝叶斯模型的显著性算法通过凸包进行图像目标区域定位,由于凸包选定的目标不够精确,含有较多背景区域,最终的检测结果不够准确,算法的适应性较差.文献[15]提出一种基于稀疏距离样本和联合上采样的颜色距离显著性检测方法,利用快速全局平滑器的边缘保持平滑和联合上采样能力,且计算运行时间短,显著性检测的准确度有所提高,但是对于复杂背景图像检测效果不是很明显.文献[16]根据像素到像素的对应关系提出一种对象感知方法,通过学习每个所选鉴别网格单元的分类器,在语义约束下指导每个像素的定位.从语义到低级估计每个像素的对应关系.文献[17]利用新颖的图形结构和背景先验,提出一种无监督的显著性检测方法,利用新的图形结构删除错误的边界种子提高检测性能.文献[18]提出基于弱监督学习的自主学习显著性检测方法,用人工标记的基础事实进行监督学习.文献[19]引入流形排序(manifold ranking,MR)算法,将显著性问题通过排序函数求解,利用前景和背景的超像素形成一个闭环图,以超像素作为图中的节点,并用MR算法比较背景和前景的相似度进行排序,进而得到最终显著图,但由于默认图像边界为背景,对于显著目标位于图像边缘的情况,检测效果不理想.
针对上述问题,对传统基于图的流形排序显著性检测算法进行改进,所提算法分为两步.第一步:对原图像进行超像素分割,得到4种不同尺度的图像,然后提取4种不同尺度图像的多特征进行上、下、左、右4个边界的显著性计算;分别将不同尺度下的4个边界显著图融合计算,得到不同尺度的显著图;最后将不同尺度的显著图进行加权融合,得到粗略显著图;第二步:将第一步中粗略显著图通过多核融合得到粗略显著图的互补显著图.融合粗略显著图和互补显著图得到最终的显著图.
1 基于改进排序的显著性区域检测算法
基于改进排序的显著性区域检测算法流程图如图1.与传统利用图的流形排序进行显著性检测算法不同的是,文中算法首先对输入图像进行超像素分割得到4种不同尺度图像,提取4种不同尺度图像的颜色特征Lab,颜色特征RGB和纹理特征LBP(local binary patterns),根据上述3种特征分别计算各个尺度图像的上、下、左、右4个方向的边界显著图,分别对各个尺度图像的4个方向的边界显著图进行融合得到各个尺度的显著图;融合4种尺度的显著图得到弱显著图;然后通过多核提升(multiple kernel boosting,MKB)算法学习来自输入图像的样本进行强分类,以检测显著像素.最后通过优化算法进一步提高检测性能.

图1 算法流程Fig.1 Algorithm flow chart
1.1 改进的流形排序显著性算法
流形排序算法[20]以图模型来模拟数据集内在的流形结构,所有的数据点通过这个图模型来将它们的排序值传播给邻接点,直到排序值收敛到稳定状态.具体算法描述如下:
给定一组点的数据集X={x1,x2,x3,…,xn}⊂Rm*n,m为特征维数,n为点的个数,其中包含了已标记的查询数据和待排序的未标记数据.令向量Y={y1,y2,y3,…,yn}T表示数据的标记情况,其中当yi=1时表示对应的数据xi为查询数据,当yj=0时表示数据xj为待排序的未标记数据.每个待排序的未标记数据xi的排序值fi由函数F:X→Rn确定.在数据集上定义一个图G=(V,E),图的结点V是数据集X,图的边缘E由关联矩阵W=[wij]n×n确定.计算图的度矩阵D=diag{d11,…,dnn},其中dii=∑wij,由于传统的流形排序算法采用单一特征计算wij,文中算法对其进行改进,采用多特征计算wij,效果要优于单一特征.具体改写公式如下:
(1)
式中:i,j∈V,dk(ci,cj)为特征空间中的超像素ci和cj之间的欧式距离,即分别为RGB(F1),CIELab(F2)颜色特征和LBP(F3)纹理特征.σ为控制边权重的常数,根据颜色空间中的距离计算权重.
对于给定的查询对象的排序得分可以通过公式(2)得到:
(2)
式中:参数u为控制平滑约束(第一项)和拟合约束(第二项)之间的平衡;fi为节点的排序值.文献[19]中已经证明流形排序函数f*最终可表示为:
f*=(D-αW)-1Y
(3)
式中:参数α=1/(1+u)决定了平滑约束(smoothness constraint)和适应性约束(sitting constraint)的权重比例.

(4)
式中:N为节点总数,由此可得到使用上边界先验的显著图Si.类似的,可以计算出使用下、左、右边界的节点作为背景种子点的显著图Sb、Sl、Sr,4个显著图融合得到不同尺度下的显著图,融合4种不同尺度的显著图得到弱显著图Sweaksal:
(5)
式中:Sfz为一个尺度下融合4个边界的显著图;Sf1为超像素分割数为100时显著图;Sf2为超像素分割数为150时显著图;Sf3为超像素分割数为200时显著图;Sf4为超像素分割数为250时显著图.
文献[19]中使用流形排序算法进行显著性检测,其采用单一的CIELab颜色特征检测和单一超像素尺度,文中采用多尺度和多特征对其进行改进,算法改进前后的对比如图2.
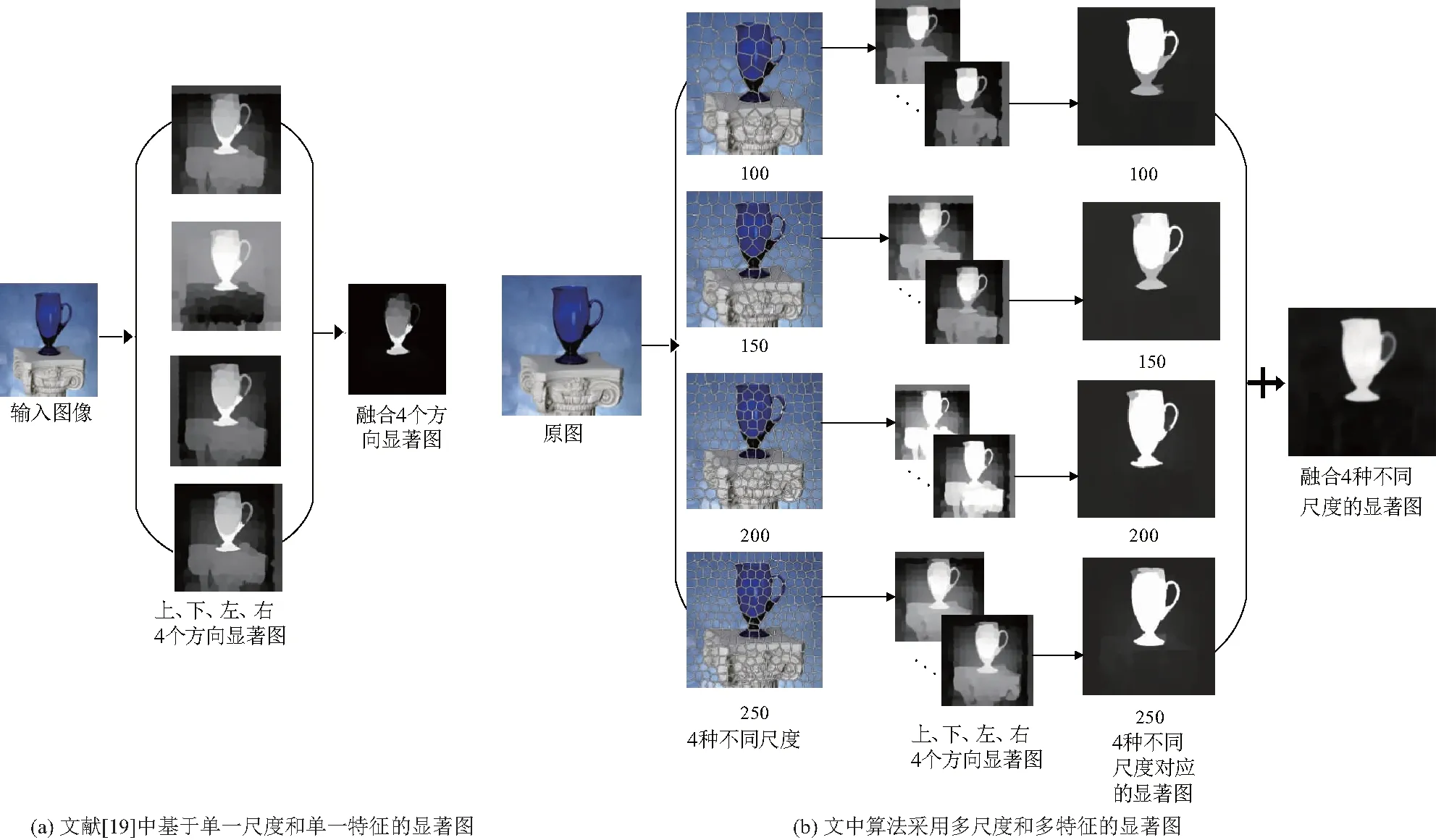
图2 算法前后对比Fig.2 Comparison example before and after algorithm improvement
1.2 多核提升(MKB)的改进显著图
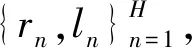
(6)
式中:βm为核权重;M为弱分类器的数量,M=Nf×Nk,Nf为特征的数量,Nk为内核的数量(Nf为3,Nk为4).
对于不同的特征集,决策函数被定义为:
(7)
式中:α=[α1l1,α2l2,…,αHlH]T,
km(r)=[km(r,r1),km(r,r2),…,km(r,rH)]T,
通过文献[18]的证明可知,决策函数最终被定义为:
(8)

Sstrong=1/4·(Sstm1+Sstm2+Sstm3+Sstm4)
(9)
由于弱显著性和强显著性具有互补性[18],所以对于弱显著图和强显著图进行加权整合,得到最终的显著性结果Sfinal,如图3.
Sfinal=σSstrong+(1-σ)Sweksal
(10)
式中:σ为组合平衡因子,σ=0.7(文献[18]中已经证明).

图3 最终显著性图对比Fig.3 Saliency maps
2 实验结果与分析
文中实验平台为2.30 GHz CPU,8 GB内存的计算机,采用Matlab(R2016b)实现.所提算法与当前主流的13和算法:SF[22],AC[23],SR[24],HDCT[25],PCA[26],GS[27],LMLC[14],FT[12],RBD[28], MR[20],GMR[19],BSCA[29],BL[18]在公开数据集MSRA1000、PASCAL-S、ECSSD上进行对比.MSRA1000是微软提供的MSRA数据库,其图像简单,单目标,但被广泛应用于比较.PASCAL-S数据集包含850幅图片,数据集来源PASCALVOC,不存在颜色的先验信息.ECSSD数据集包含1 000幅图像,是对CSSD的扩展,图像背景复杂,存在多个显著性物体.3个数据集均由人工精确标注显著目标.文中从客观性能评价和主观性能评价两个方面对所提算法的性能进行测试.客观性能评价为通过准确率(P)、召回率(R),算法综合指标(F)和与其他13种算法进行评估.在实验中,对于一幅显著图Sfinal,将Sfinal通过阈值Tf∈[0,255]依次调整进行二值化,得到二值图M,GT表示Ground-truth.根据公式(10、11)计算准确率和召回率,值由公式(12)计算得到.
(10)
(11)
(12)
与文献[10,20]一致,其中β取值为0.3.图4~6为所提算法和其他算法分别计算准确率-召回率,综合指标的对比结果图.
图4是各种算法在MSRA1000数据集上的对比结果,可以发现文中算法在准确率-召回率与RBD算法较为接近,远高于MR、GMR,BL等算法.
通过图7(a)可以发现文中算法在准确率要优于GS、HDCT、GMR等算法,与BSCA、BL算法较为接近,且综合指标远高于其他12种算法.
图5是各种算法在ECSSD数据集上的对比结果,可以发现在复杂背景下,文中算法的准确率接近或优于目前流行的显著性检测算法,与HDCT算较为接近,但是文中在召回率远高于HDCT算法,检测效果也远高于对比的其他12种算法.由图7(b)柱状图可以发现文中算法在复杂背景下检测效果略好于BSCA和GMR算法,且高于HDCT算法.由于ECSSD数据集中多为复杂背景图像和多目标图像,所以检测效果略低于MSRA1000数据集.

图4 MSRA1000数据集上PR曲线的比较Fig.4 Comparison of PR curve on MSRA 1000

图5 ECSSD数据集上的PR曲线的比较Fig.5 Comparison of PR curve on ECSSD
图6是各种算法在PASCAL-S数据集上的对比结果,可以发现文中算法的准确率-召回率与RBD算法接近,优于其他12种对比的算法(图7(c)).

图6 PASCAL-S数据集上的PR曲线比较Fig.6 Comparison of PR curve on PASCAL-S
文中算法与上述13种算法的视觉效果比较,如图8,可以看出文中算法对比度更好,且具有很好的视觉效果,能够很好的抑制图像背景区域并且清晰突显著区域,与真值图非常接近.通过直观效果可以发现与文中算法显著图最接近的是HDCT、GMR、BL和BSCA算法,但是文中算法显著图比HDCT和BL更加平滑,能够更好的抑制背景,检测的轮廓更加完整.同时,BSCA算法对于复杂背景图像的检测不如文中算法检测的完整.

图7 与其他算法比较的准确率、召回率和算法综合指标的柱状图Fig.7 Comparision of PR curve and F-measurewith other methods

图8 各种算法的显著性对比图Fig.8 Comparison of saliency map
3 结论
文中基于改进流行排序算法的显著性区域检测,将图像分割成4种不同的超像素尺度,并根据图像的RGB,CIELab的颜色特征和LBP纹理特征分别计算4种尺度图像的上、下、左、右4个方向的边界显著图,分别融合不同尺度图像的4个方向的边界显著图得到相应不同尺度图像显著图,融合4种尺度图像的显著图得到弱显著图;然后根据弱显著图以生成强模型的训练样本,通过多核提升算法学习来自输入图像的样本进行强分类,以检测显著像素;最后综合多尺度显著图进一步提高检测性能,并进行优化处理得到最终的显著图,从而解决了基于图的流行排序算法相关显著性检测算法对与检测的显著目标不完整且不能更好的抑制背景的问题.在公开数据集MSRA1000、ECSSD和PASCAL-S上进行的实验结果表明,所提算法不仅能够得到较好的视觉效果,而且召回率、准确率和算法综合指标等评价指标优于或接近于流行的显著性检测算法,尤其对于复杂背景图像的检测,其检测结果都优于目前流行的显著性检测算法.但该算法在复杂背景检测方面还存在不足,还有待进一步提高.下一阶段工作将会对提高复杂背景图像检测准确率进行研究改进.
