基于数学形态学的三端柔性直流系统仿真研究

2020-07-21黄琳

通信电源技术 2020年8期

黄琳

（湖北工业职业技术学院，湖北十堰 442012）

0 引言

柔性直流输电共经历了换流器为两电平结构、换流器为三电平结构、模块化多电平换流器3个阶段，在换流器为两电平结构阶段一般采用正弦脉冲宽度调制（SPWM）方式，直流系统的电压可以达到±80 kV，ABB公司掌握了该发展阶段的核心技术。由于两电平方式自身的局限性如电压等级低、开关损耗大等，所以在实践中的应用较少。在换流器为三电平结构阶段，开关频率约降为两电平的一半，在很大程度上提升了柔性直流工程的输送功率及电压等级。在模块化多电平换流器阶段采用MMC换流器，采用调制的方式降低开关频率，降低开关损耗，同时模块化设计的制造难度低，受到关注。不同于常规直流输电，柔性直流技术采用可关断器件，构成无源逆变形式，无换相失败情况，进而可以连接无源网络。此外，柔性换流器有功无功解耦控制实现简单、方便，功率翻转的实现也非常容易，在构建柔性直流供电多端系统时，电压极性的改变根本不用考虑。

虽然柔性直流输电技术有很多优势，但也存在控制方法复杂的缺点。因此，本文采用数学形态学方法对柔性直流系统进行仿真分析，以期提高柔性直流输电技术的控制效果。

1 数学形态学基本原理

定义1：假设某个图像B，该图像沿着矢量ɑ（x0，y0）平移某段距离，这个过程可以称之为B的平移。记作B0={b+ɑ|b∈B}。

定义2：图像B的对称集合为B相对于图像原点的反射。记作Bv={-b|b∈B}。

定义3：如果结构元素B平移ɑ后属于X中的任何一个点，则记录ɑ点，记录全部的ɑ点得到一个集合，则可以说这个集合就是X被B腐蚀的结果，即：由B对X腐蚀所产生的图像E中的点（x，y）满足：如果B的原点平移到点（x，y），那么B将完全包含于X中。记作：E（X）=XΘB={ɑ|B⊂X}。图1为腐蚀的示意图。

定义4：腐蚀的对偶运算为膨胀，将结构元素B平移ɑ后得到Ba，如果Ba击中X，则记下这个ɑ点，ɑ点组成的集合称做X被B膨胀的结果。如果B的原点平移到点（x，y），那么它与X的交集非空。记作D(X)=X⊕B={ɑ|Ba↑X}。图2为膨胀的示意图。

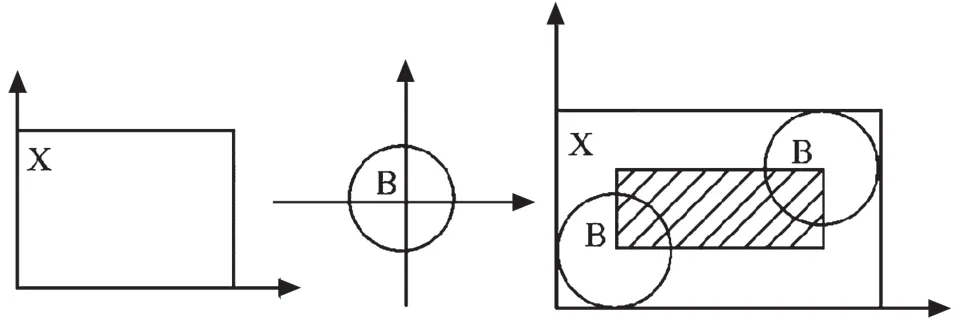
图1 腐蚀的示意图

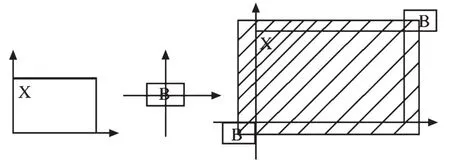
图2 膨胀的示意图

2 多尺度形态滤波（MMF）算法

采用多尺度形态滤波方法对信号进行处理，主要是因为MMF具有如下优势。第一，通过MMF对信号进行处理，可以快速获得信号的突变方向和突变时刻，用时较低；第二，MMF不用进行乘除操作，因此，处理速度较快，简单、便捷，并且对于非周期暂态信号的处理效果较好；第三，能够精确的对信号进行提取，失真度较低，操作简单，在时域操作并不需要积分变换；第四，与WT、HHT等方法相比，MMF具有很强的抗噪声能力，对于采样频率要求不高，不需要全部的信号成分信息。

形态学操作最主要的功能是提取两个系列集的相关结构，后一个系列集称作结构元素SE（Structuring Element）。对最基本膨胀和腐蚀的对偶形态学操作进行定义，结果如下：

其中，⊕、⊗分别代表膨胀操作、腐蚀操作；h为待处理的信号，g代表信号SE，h的长度比g长；Xh为h的定义域，Xg为g的定义域。形态学滤波是对信号进行非线性的变化，通过非线性的变化将信号的几何特征进行改变。对膨胀和腐蚀组成的开运算和闭运算进行如下定义：

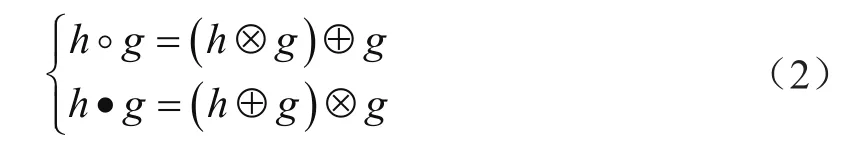
其中，○、●分别代表开运算（定义先腐蚀后膨胀）、闭运算（定义先膨胀再腐蚀）。开运算和闭运算二者形成一对对偶运算。开运算可以实现正脉冲信号的平滑，闭运算可以将负脉冲信号的裂缝和低谷填平。通过上面的各种操作，可以实现信号的多尺度形态滤波，通过多尺度滤波对形态的突变点进行检测，但是这种方法也有一个缺点，即不能实现信号突变方向的检测。虽然部分学者通过特定的语句判断对信号突变进行检测，但是这种算法比较繁琐，所以，定义了一种比较新颖的MMF：

3 基于数学形态学的三端柔性直流系统仿真研究

3.1 多端直流输电系统的优势及应用领域

与传统的直流输电相比，柔性直流输电工程根据不同的结构可以分成两类，一类是两端柔性直流输电，与交流系统相连接时只有两个端口，每个端口处连接一个换流站；另一类是多端柔性直流输电，它与交流系统的连接至少有三个端口，每个端口连接一个换流站。现阶段应用的双端直流输电系统，只能实现点对点的功率传送，对于多电源供电的需求不能满足，并且如果其中一端的换流站出现某种故障将会直接导致整个直流系统的瘫痪，而多端系统可以解决这些问题。和两端输电系统相比，多端直流输电系统可以实现多电源供电和多落点受电，更加经济。由于柔性直流输电在潮流翻转时，具有直流电压极性不变、直流电流方向反转的特点，所以对于并联多端直流输电系统的构成十分有利。柔性多端直流输电系统的成本低、供电可靠，应用灵活，主要应用的领域包括分布式发电、可再生能源发电、孤岛供电及城市供电[1]。

3.2 三端柔性直流仿真系统

多电平换流器（MMC）的换流站每个桥臂包含多个半桥子模块，这些半桥子模块串联在一起。桥臂中还串联有桥臂电抗器，桥臂电抗器具有抑制环流的作用。直流侧发生故障之后，MMC做出如下动作：通过绝缘栅双极型晶体管半桥子模块闭锁前电容快速放电，半桥子模块闭锁之后交流系统馈入短路电流，半桥子模块二极管同时续流导通交替馈入稳态短路电流。在仿真过程中，采用“MMC+高压大容量直流断路器”技术路线。系统仿真拓扑如图3所示。

整个系统采用小电流的接地方式。当系统运行稳定时，换流站A和换流站C注入的有功功率分别为300 MW、200 MW，换流站B对有功功率进行吸收，吸收的功率为500 MW。如果发生单极接地故障则产生的短路电流不大。因此仿真分析中以双极短路故障为例，直流电压150 kV；额定容量100 MW；电感30 mH；电容250 μF；整流侧变压器220 kV/115 kV；逆变侧变压器65 kV/220 kV；直流线路电阻2 Ω。仿真过程中设置两种控制策略，一是利用VSC为直流电压控制端的控制策略，控制中采用多尺度形态滤波（MMF）算法；二是选取LCC作为直流电压控制端的常规控制策略[2]。

系统稳态时的仿真结果：采用策略一时，直流系统达到稳定状态需要的时间大约为0.1 s，采用策略二时直流系统达到稳定状态需要的时间大约为0.3 5 s，两种情况的直流线路电压在150 kV附近。策略一需要的控制时间最短。在初始阶段，策略一能够保证直流电压稳步上升直至达到额定值，对于充电过电流的现象有明显的抑制作用。策略二进行控制时初始阶段有短暂的过电流现象。由此可知，多尺度形态滤波（MMF）算法对三端柔性直流系统进行控制，效果较好。