基于强度理论的扭力梁支架失效有限元分析及优化

谷昆仑 ， 郝朝利 ， 程 啸

（江苏吉麦新能源车业有限公司，江苏 徐州 221011）

0 引言

汽车悬架系统的主要作用是传递作用在车轮和车身之间的力和力矩，缓冲路面传递给车身的冲击载荷，并衰减由此引起的振动，保障驾驶员及乘客的舒适性[1]。纯电动车型在试验场进行强化路试验，行驶约9 000 km 时发现车身后部出现异响，轮胎跳动轨迹出现异常，经检查发现后悬架扭力梁车身侧支架出现多处裂纹及开裂现象。

传统意义上的研发流程，需通过大量的试验验证设计方案的可行性，不但开发周期长，同时还增加了各种成本开支。如通过有限元分析来优化改进结构，不仅可以提高产品设计的效率，同时还可以缩减试验验证周期，降低研发成本。目前，国内外文献中不乏关于扭力梁的有限元分析案例，鲜见关于扭力梁车身侧支架开裂有限元分析案例。关于扭力梁支架开裂有限元分析需注意分析建模、载荷工况、试验对标及结果判定标准等事项。

本研究通过运用有限元分析的方法建立有限元模型，通过加载典型工况，运用强度理论判据，分析危险位置，然后针对危险位置提出优化方案，提高支架强度。跟踪路试试验，验证方案的可行性。

1 试验结果分析

纯电动车型在试验场进行强化路试验过程中，后扭力梁与车身连接侧的支架出现开裂，如图1所示。经分析总结，发生开裂的主要原因有：1）由于支架根部与车身缺少焊接焊点，导致载荷无法完全传递到车身纵梁上，如图1 中A 所示；2）由于支架与两侧连接较少，导致支架载荷无法向两侧传递，如图1 中B 所示；3）由于支架前部支撑过弱，载荷传递不畅，导致支架前部出现开裂，如图1中C 所示。

图1 后扭力梁支架试验开裂图Fig.1 Failure of back torsion beam supportaftertest

2 强度理论

强度理论主要有4 种常用的强度理论，第三强度理论和第四强度理论一般用于评价和解释塑性材料屈服的强度理论[2]。其中，第三强度理论和第四强度理论公式分别如式（1）、式（2）所示：

式中：σ1、σ2、σ3分别为第一、第二、第三主应力；σ 为许用应力。

根据参考文献[3]得出主应力的计算公式如式（3）～式（5）所示：

式中：

其中，σx、σy、σz、τxy、τyz、τzx分别为单元体3 个方向上的正应力和切应力。

由以上公式可以看出，相比第三强度理论，第四强度理论将主应力σ2考虑其中，对于薄壁结构承受复杂载荷的应力状态，采用第四强度理论作为判据，结果更贴近了实际状态，减小了误差，因此，本研究选用第四强度理论进行评价。

3 有限元模型

在有限元分析过程中，模型合理的简化对分析过程和分析结果的影响至关重要。针对不同的求解类型，有限元模型建立的侧重点也略有差异。一般应在保证计算精度的前提下，尽可能缩短建模和求解计算的时间。

考虑到整车模型较大，对整车模型进行简化，选取车身的三维模型并通过有限元前处理软件搭建分析模型；有限元模型的零部件网格平均尺寸为5 mm，同时为了提高仿真分析的精度，对后扭力梁支架的网格进行细化；车身相关的钣金件采用壳单元建立车身有限元模型，焊点采用ACM 单元进行模拟，螺栓、焊缝采用RBE2 刚性单元进行简化处理，配重质点CONM2 采用RBE3 连接[4]，有限元模型如图2 所示。

4 边界条件

为了更好地找寻后扭力梁支架在道路试验中开裂的根本原因，同时结合以往分析经验[5-8]，本研究简化为主要考虑车辆在路面行驶的3 种比较典型的恶劣工况，如图3 所示：

工况1：垂向冲击工况，表示车辆承受垂直方向上跳3 g 加速度时的状态（图3a）；

图3 边界条件和载荷Fig.3 Boundary condition and loads

工况2：前行制动工况，表示车辆在制动过程中承受1 g 加速度的状态（图3b）；

工况3：转弯工况，表示车辆在转弯过程中承受侧向1 g 加速度的状态（图3c）。

为了更好地模拟扭力梁支架在各种路面工况下的真实受力，首先通过动力学分析软件提取底盘与车身连接的各个硬点的力和力矩作为载荷输入。然后在分析中引用惯性释放的原理完成计算[9-13]，获取扭力梁支架的应力分布。3 种工况的加载模型如图3 所示。

5 对标分析结果

模型经计算完毕后，首先通过后处理检查零部件是否有异常运动及运动穿透情况，确认模型计算无问题。

基于第四强度理论，通过查看各个工况下的后扭力梁支架应力云图，可以发现：

1）垂向冲击工况下，后扭力梁支架与纵梁搭接处应力较大，最大应力为372 MPa，超出材料的许用应力340 MPa，存在开裂风险（图4a）。这与道路试验图1 中A 开裂位置一致。

2）前行制动工况下，后扭力梁支架与纵梁搭接处、支架内侧、支架前端的应力均较大，最大应力为1000 MPa，均超出材料的许用应力340 MPa，存在较大开裂风险（图4b）。这与道路试验图1 中A、B、C 开裂位置一致。

图4 各工况下应力分布云图Fig.4 Stress distribution under working conditions

3）转弯工况下，后扭力梁支架前端及根部与纵梁搭接处的应力均较大，最大应力值为590 MPa，均超出材料的许用应力340 MPa，存在较大开裂风险（图4c）。这与道路试验图1 中A、C 开裂位置一致。

从以上3 个工况的分析结果可以看出，仿真分析结果较好地反映出道路试验后扭力梁支架的失效的位置及状态，进一步说明有限元模型的可靠性。

6 结构优化

考虑尽可能少的改变原结构基础上进行结构优化，基于以上对标模型及结果对后扭力梁支架结构，进行以下优化：

1）增强扭力梁支架底部与纵梁的连接，如图5中A、B 所示；

2）增加支架与周围零件的连接，传递来自地面的冲击载荷，如图5 中B、C 所示。

图5 原始方案和优化方案Fig.5 Initial structure and improved structure

根据以上优化方案，重新建立模型并递交计算，通过计算后处理得到的应变云图如图6 所示。结果表明，优化后的模型，3 个工况的最大应力均未超过材料的许用应力340 MPa，且安全系数大于1.2。后扭力梁支架强度满足法规要求。

基于以上优化方案进行样件样车试制，重新进行道路可靠性耐久试验，在完成规定里程道路试验后检查后扭力梁支架，没有发生任何开裂，进一步验证了方案的有效性。

7 结论

1）运用有限元手段进行模型的合理简化、局部细化网格、道路工况合理简化、动力学分析软件载荷提取、惯性释放理论等，对标后扭梁支架道路试验开裂结果，分析结果显示后扭梁支架强度风险位置与试验开裂位置吻合度较高。

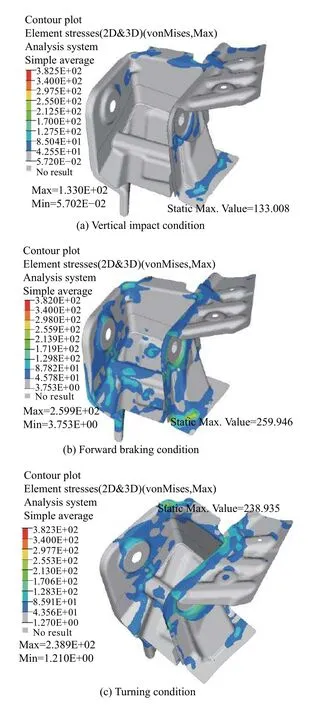
图6 优化方案各工况下应力分布云图Fig.6 Stress distribution of improved structure under working conditions

2）针对典型工况强度分析中的危险位置提出优化方案，提高支架结构强度，通过提高支架的强度和传递支架的载荷，能够有效改善支架结构的应力分布。进一步跟踪路试耐久试验，验证方案的可行性。

3）通过利用CAE 分析技术在车辆开发过程中的应用，能够有效找到问题原因并有针对性地加以优化，从而缩短开发周期和节约成本。