基于SIR模型对新冠肺炎的预测

张佳琪 谭立超

最近新冠肺炎的大面积爆发对我国公民的生命和财产安全造成了极大的隐患，为了对新冠肺炎的传播规律进行预测，本文采用SIR模型来模拟新冠肺炎的发展曲线，根据测试得到的曲线来推导新冠肺炎的发展趋势，并对此进行监测和预警。本文首先对SIR模型进行了简要介绍，之后根据新冠肺炎的传染规律，利用SIR模型对其进行了数学建模，通过对模型的分析，即可得到新冠肺炎的发展历程，从而对其进行有效的预防。

一、引言

流行病预测是令世界各国比较头疼的问题，虽然在十八世纪就有数学家利用数学模型来对流行病进行预测的例子存在，但是世界上真正开始对流行病进行研究的课题还是在两个世纪之后才形成的。在1906年，为了对麻疹的传染规律进行预测，Hamer博士设计了一个机遇离散时间的数学模型来分析其发展规律，从而开启了人们利用数学模型来对传染病进行分析的历史。由于传染病的传播规律是连续的，所以Ross博士采用微分方程来对传染病进行分析，得到了比较好的结果。在1920年前后，由Kermack和McKendrick博士设计了一个名为SIR的数学模型来对给伦敦造成深远影响的黑死病进行预测，该模型创新性地将人口结构分为了易感染人群（S）、感染人群（R）以及移出者人群（R），通过对三种人群的动态变化的研究，来模拟流行病的发展规律，得到了很好地结果，并成为了目前对流行病进行预测时的一种良好的数学模型。

二、SIR模型简介

SIR是一种基于仓室的数学模型，该模型将人口结构划分为了三种状态，三种状态可以用下面的数学公式进行表示：

易感染人群。使用 S （t） 进行表示，代表在任意时刻没有患上传染病，但是有很大可能患上传染病的人群数量。

感染者人群。使 I （t） 进行表示，代表在任意时刻患上传染病的人群数量。

移出者人群。使用 R （t） 进行表示，代表在任意时刻从感染者人群中移出的人数。

SIR数学模型在对传染病进行分析时，是具有先决条件的，首先，SIR模型考虑人口的出生和死亡，这两者可能对人口的数量造成影响，但是影响十分小。其次，SIR模型假设易感染人群和感染者人群具有一定的流动性，易感染者人群会以某个因子向感染着人群进行迁移。最后，SIR模型假设感染者人群会以固定的比例系数进入移出者人群，并且状态不可逆。所以根据如上所示的假设，可以得到下面的SIR模型状态迁移图：

图1 SIR状态迁移图

图1给出了SIR模型的状态迁移图，图中bSI表示易感染者人群向感染者人群的人口迁移数量，gI表示感染者人群向移出者人群的人口迁移数量。通过对状态迁移图的分析，可以得到如下所示的SIR数学模型：

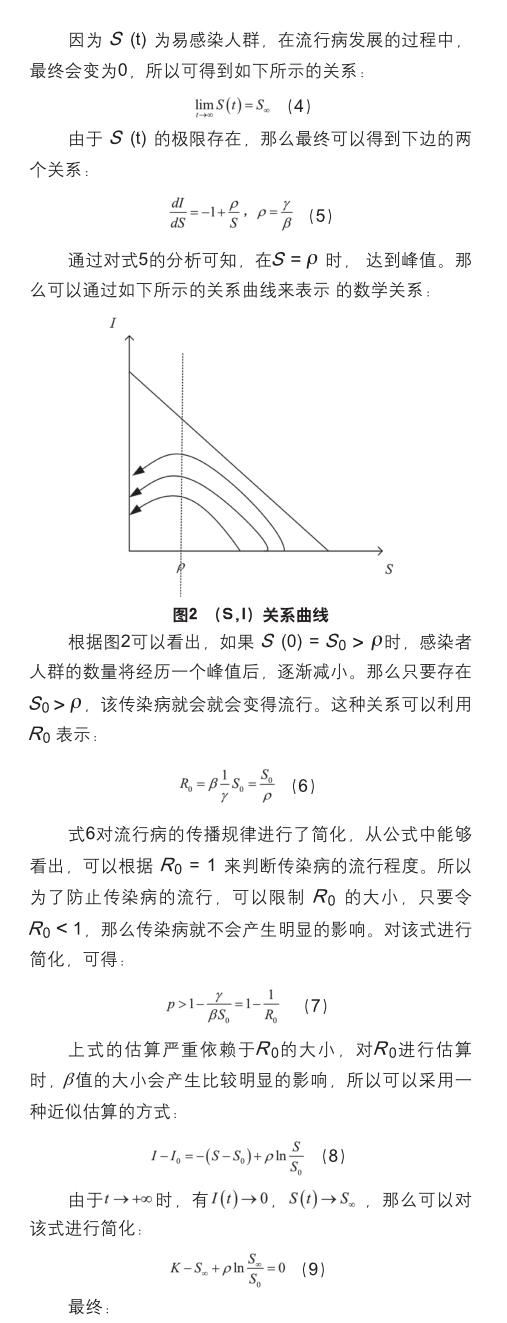
图3 病人治愈率曲线

图4 病人死亡率曲线

表1給出了SIR模型的数值变化表：

表1 SIR模型数值变化表

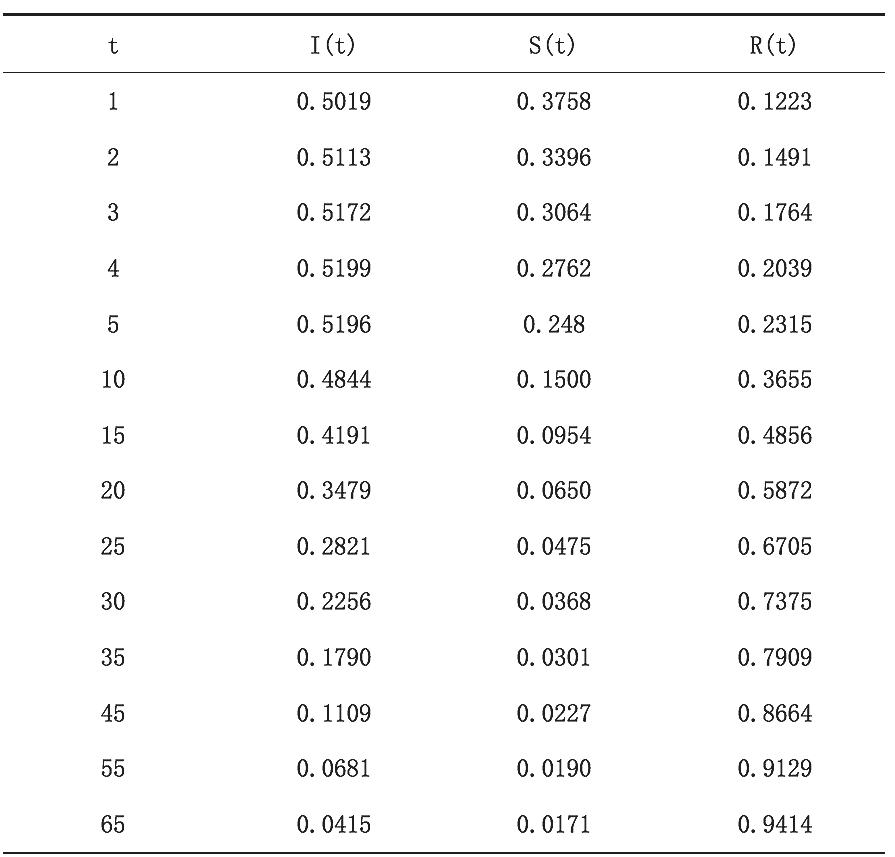
从上表可以看出， I （t） 从初始值到达第四天的时候，到达峰值，而S （t） 则处于单调递减的状态。为了方便展示，图5给出了对应的数值变化曲线。

从图5中可以看出，R （t） 处于单调递增的状态，表示移出人群的数量在不断递增， I （t） 在经历一个峰值后逐渐减小， S （t） 则处于单调递减状态，表明处于易感染的人群数量在不断地向移出转态人群过渡。仿真结果表明，这种现象符合新冠肺炎的传播规律，从新冠肺炎开始爆发到逐渐平稳的过程大概经历了两个月的周期。图6给出了本文的预测结果与实际数据的对比示意图。

本文预测到新冠肺炎在武汉地区经过两个多月的防控后，疫情状况逐渐趋于稳定，而观察历史数据也可以发现，疫情的发展情况在经过两个月左右的防控后，确实已经进入了尾声。

图5 SIR数值变化曲线

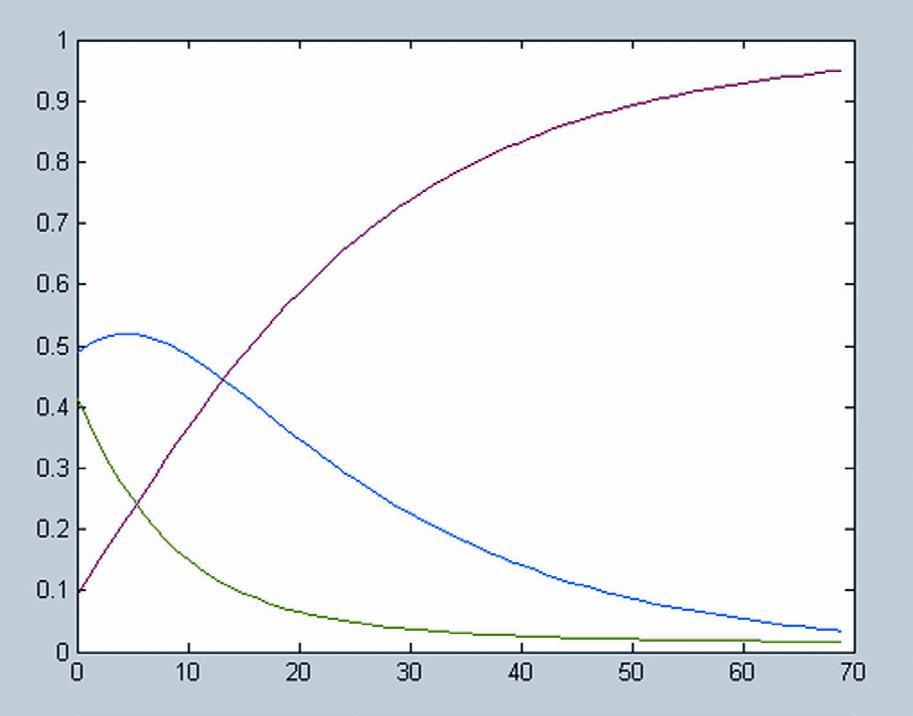
图6 数据拟合测试结果

五、结论

SIR是一种有效的传染病模拟模型，通过将人口结构划分为易感染人群、感染人群和移出人群来对传染病的传播规律进行简化，可以得到比较准确的传染病传播规律。考虑到SIR模型的这一优势，本文利用SIR模型来对武汉地区的新冠肺炎发展规律进行了数学模拟，模拟结果表明，本文的测试结果与实际的疫情发展规律比较符合，大概在两个月左右的时间范围内，疫情将会得到有效的控制。

作者单位：湖北警官学院