指数函数性质的再探究

◇ 上海 陈羿男

1 已有结论

指数函数涉及日常生产生活的很多方面，例如细胞分裂、贷款利率的计算等，因此，对指数函数性质的学习具有很大的现实价值.

在对指数函数现有的研究中，已有很多成熟的结论，例如指数函数的函数值分布规律、底数对指数函数图象位置的影响等，但基本都是文字语言的描述或者需要进行分类讨论.因此，我们可以尝试用更简洁的文字或符号语言来描述指数函数的相关性质.

2 深入探究

对于指数函数y=ax，为了使x 可以在实数范围内取值，对于底数a 的范围需要限制为a＞0且a≠1.对此，我们可以这样理解：如果a=1，那么其非奇非偶性及单调性都会被破坏，为了保证指数函数性质的纯粹性，规定指数函数的底数a＞0且a≠1.

底数a 的不同取值会对指数函数的图象和性质有影响，具体表现在以下几个方面.

2.1 底数a 的不同取值对指数函数函数值分布规律的影响

对于指数函数y=ax（a＞0且a≠1），其函数值的分布规律可以归纳如下.

（1）当a＞1时，①当x＞0时，ax＞1；②当x＜0时，0＜ax＜1；

（2）当0＜a＜1时，①当x＞0时，0＜ax＜1；②当x＜0时，ax＞1.

由于指数函数y=ax（a＞0 且a≠1）的值域为（0，+∞），因此我们更加关注ax与1的大小关系，探究底数a 与指数x 分别满足不同条件时，ax与1的大小关系.所以，指数函数函数值的规律可以总结为：（1）当a＞1且x＞0，或0＜a＜1且x＜0时，ax＞1；（2）当a＞1且x＜0，或0＜a＜1且x＞0时，0＜ax＜1.

当底数a 和1与指数x 和0之间的不等号同向，即（a-1）x＞0时，ax＞1；当底数a 和1与指数x 与0之间的不等号反向，即（a-1）x＜0时，0＜ax＜1.为避免分类讨论，可以将底数a 和1，指数x 和0，以及ax和1之间的关系归纳为（a-1）x（ax-1）＞0.由此即可分析出a，x 在不同取值区间的函数值变化规律.

2.2 底数a 的不同取值对指数函数图象位置的影响

通过观察图象，可以得出结论：底数互为倒数的两个指数函数图象关于y 轴对称.此外，当底数a＞1时，a 的值越大，图象越靠近y 轴；当底数0＜a＜1时，a 的值越小，图象越靠近y 轴.两个底数互为倒数（即两个底数a1，a2满足a1a2=1）的关系是比较特殊的，因此，我们探究两个底数满足更一般的关系时，图象与y 轴的靠近程度.这里，我们将图象与y 轴的靠近程度表达为：两个指数函数与（其中a1，a2＞0 且a1，a2≠1）的函数值相 同 时，对 应 的越小，则函数图象越靠近y 轴.即研究当=时，对应的｜x1｜，｜x2｜的大小关系，以此得出两个指数函数图象与y 轴的接近程度.由于，等式两边分别取对数，得x1·lga1=x2·lga2，｜x1｜=｜x2｜·｜loga1a2｜，因 此｜x1｜，｜x2｜的 大 小 关 系 由｜loga1a2｜与1的大小决定.设a1＜a2，并对两个底数a1，a2的关系进行分类，分别有以下几种情况：

（1）当0＜a1＜a2＜1时，由图1可得｜x1｜＜｜x2｜，即底数越小，函数图象越靠近y 轴；

（2）当0＜a1＜1＜a2且a1a2＜1时，由图2可得｜x1｜＜｜x2｜，即底数越小，越靠近y 轴；

（3）当0＜a1＜1＜a2且a1a2=1时，｜x1｜=｜x2｜，则两个图象关于y 轴对称；

（4）当0＜a1＜1＜a2且a1a2＞1时，由图3可得｜x1｜＞｜x2｜，即底数越大，越靠近y 轴；

（5）当1＜a1＜a2时，由图4可得｜x1｜＞｜x2｜，即底数越大，函数图象越靠近y 轴.

图1 函数y=0.3x与y=0.4x 图象

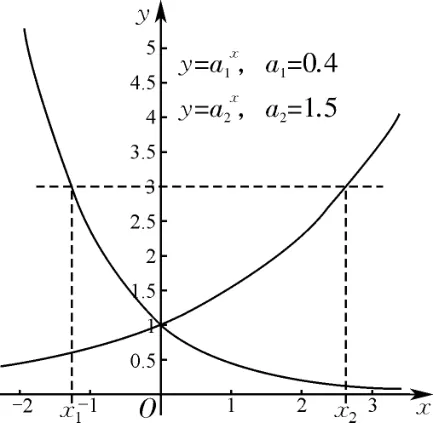
图2 函数y=0.4x与y=1.5x 图象

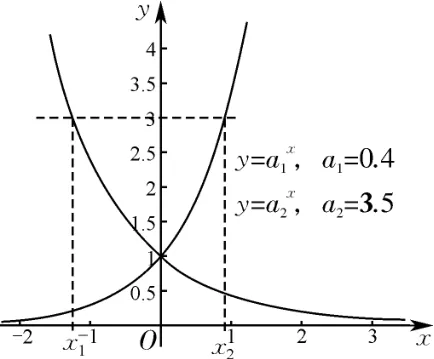
图3 函数y=0.4x与y=3.5x 图象

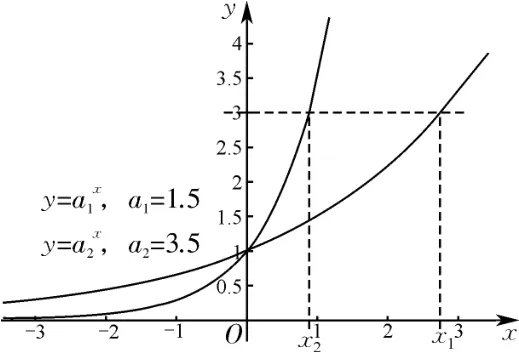
图4 函数y=1.5x与y=3.5x 图象

可以概括为：

（1）当0＜a1a2＜1时，底数越小，对应图象越靠近y 轴；

（2）当a1a2=1时，两个图象关于y 轴对称，两个图象离y 轴一样近；

（3）当a1a2＞1时，底数越大，对应函数图象越靠近y 轴.

当底数a 从0趋向于无穷大的过程中（a≠1），函数图象从接近于y 轴和x 轴的正半轴的单调递减的曲线，逐渐变为接近于y 轴正半轴与x 轴负半轴的单调递增的曲线.而直线y=1则是图象从单调递减到单调递增的过渡状态.

图象与y 轴的靠近程度表明了图象在横向方向上呈现的规律，此外又进一步研究了图象在纵向方向上呈现的规律，即研究函数与（其中a1，a2＞0且a1，a2≠1）在取相同自变量时，对应函数值的大小关系，以此得出两个指数函数图象的高低.我们将图象的高低表达为：两个指数函数y=与y=（其中a1，a2＞0且a1，a2≠1）取相同自变量值x=m 时，对应的函数值与的值）越大，则函数图象越高.设a1＜a2，则通过函数思想分析，结合幂函数y=xm（m 为常数）在第一象限的单调性，可得：当m ＞0 时，即，即对于指数函数和而言，在第一象限，满足“底大图高”；当m ＜0时1，即，在第二象限，满足“底小图高”；当m=0时，即指数函数和都经过点（0，1）.

3 研究结论

指数函数y=ax（a＞0且a≠1）函数值的分布规律可以简单地归纳为（a-1）x（ax-1）＞0，避免了分类讨论.用精准的数学方式表达底数a 对指数函数图象位置的影响，主要分为以下两种：一是纵向上的影响，在第一象限，满足“底大图高”；在第二象限，满足“底小图高”.二是横向上的影响，对于指数函数y=和y=（其中a1，a2＞0 且a1，a2≠1）而言，当0＜a1a2＜1 时，底数越小，对应图象越靠近y 轴；当0＜a1a2=1时，两个图象关于y 轴对称，两个图象离y 轴一样近；当a1a2＞1时，底数越大，对应函数图象越靠近y 轴.