结合克拉默法则求解齐次多元隐函数方程组的偏导数

龙彩燕

(广州工商学院 基础部，广州510000)

0 引言

克拉默法则在求解非齐次线性方程组中起着非常重要的作用，是一个计算简便的方法，特别是对于二元、三元的齐次线性方程组的求解可以利用行列式计算表示。关于一元隐函数求导的研究成果有很多，对于多元隐函数求偏导数也有比较显著的成果，是高等数学教学的一个重点，也是难点。而多元隐函数方程组的偏导数求解则是难中之难。下面，利用克拉默法则求解齐次多元隐函数方程组的偏导数。

1 回顾克拉默法则定理及例题应用

定理1：

(克拉默法则)如果线性方程组(1)

的系数行列式

则方程组(1)有唯一解且解为

其中Dj是将系数行列式D中j列的元素用方程组右端的常数项代替后所得到的n阶行列式，即

例1：用克拉默法则求解线性方程组：

2 利用克拉默法则求解多元齐次隐函数偏导数方程组

多元齐次隐函数偏导数方程组是指隐函数关于其中一个自变量的偏导个数与方程的个数相同。

定理2：

隐函数方程组

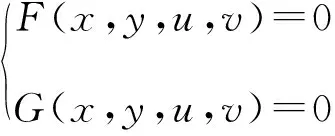
两边同时对x(或y)求导且整理为

其中a11,a12,a21,a22,b1,b2为关于x,y,u,v的函数，只要

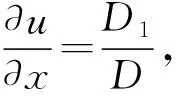
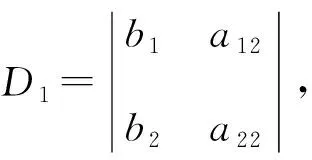
例2 ：

解：将方程组两边同时对x求导，得

则令a11=x2,a12=-y3,a21=y,a22=x,b1=-2xu,b2=-v，只要系数行列式

同理得