非能动加速的驱动线落棒特性仿真研究
2020-07-20陈训刚莫锦涛颜达鹏沈月音牛昊轩
陈训刚 莫锦涛 罗 英 颜达鹏 沈月音 牛昊轩
(中国核动力研究设计院 核反应堆系统设计技术重点实验室 成都 610213)
ACP100S模块式浮动反应堆为适应海洋环境,在原模块式小型堆ACP100的驱动线上增设了弹簧,使控制棒落棒由自由下落变为非能动加速下落,以便在倾斜和摇摆的状态下获得理想的落棒时间。
控制棒落棒是一个复杂的过程,由于弹簧作用的不确定性,直接通过驱动线冷态、热态和摇摆试验来测得落棒时间和冲击力,将会给反应堆的设计带来很大的风险;再加上弹簧的刚度和作用长度选取的问题,会导致设计和试验成本大幅增加。因此,有必要在试验前对弹簧作用下的驱动线落棒行为进行仿真研究,一方面可以优化结构,降低设计风险;另一方面可以确定试验目标,缩小试验范围,从而减少试验时间,降低试验成本。
目前驱动线仿真主要有一维水力模型和动网格模型。一维水力模型在工程上取得了较为广泛的应用,有些学者[1-2]为了对核电站压水堆控制棒落棒时间进行计算,基于一维水力模型研制开发了相应的专用软件。另外一种方法是计算流体力学(Computational Fluid Dynamics,CFD)动网格计算方法。例如,肖聪等[3]基于CFD动网格技术,对某反应堆的驱动线导向组件以及单根控制棒建立了相应的三维流体仿真模型。还有一些学者[4]为了在仿真中更精确地考虑机械摩擦力的作用,提出了“一维流体+三维机械”的动力学仿真方法,且更进一步考虑了非竖直工况的落棒过程[5]。但目前的耦合仿真模型均限于控制棒能动的自由落棒,未考虑弹簧这种非能动加速的方式对驱动线落棒的影响。
本文在文献[6]一维水力模型基础上,对弹簧的作用力进行了考虑,并对ACP100S驱动线典型工况下的落棒行为进行了仿真研究。
1 驱动线落棒计算模型
ACP100S驱动线主要由驱动机构、驱动杆、驱动杆保护管、弹簧、控制棒导向筒、控制棒组件和燃料组件组成,如图1所示。
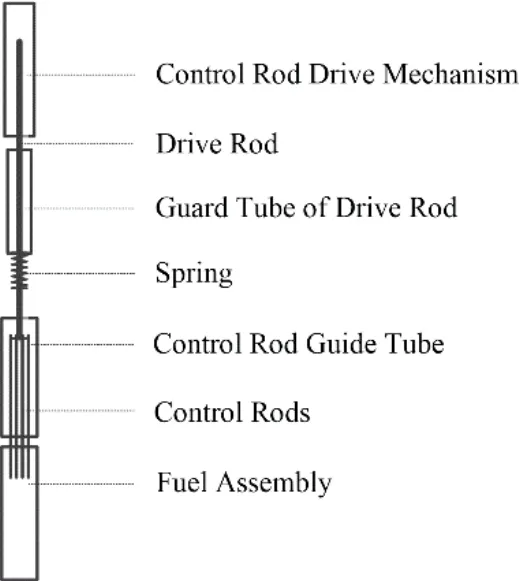
图1 ACP100S驱动线简化模型示意图Fig.1 Schematic diagram ofACP100S drive line simplification model
燃料组件为截短的AFA 3G组件,内部的导向管下端设置有缩径段,缩径段底端和靠近缩径段上端的导向管侧面均开有细小的流水孔,在控制棒落棒末期可以实现水力缓冲。驱动杆连接着24根控制棒,在驱动机构的作用下,带着控制棒在燃料组件和控制棒导向筒的导向管内上、下运动。弹簧设置在驱动杆保护管下端,当控制棒提至最高位时,弹簧被压缩,驱动机构释放后,控制棒在重力和弹簧力的共同作用下加速落棒,驱动线受力情况如图2所示,其中Fn为导向结构对运动部件的正压力。
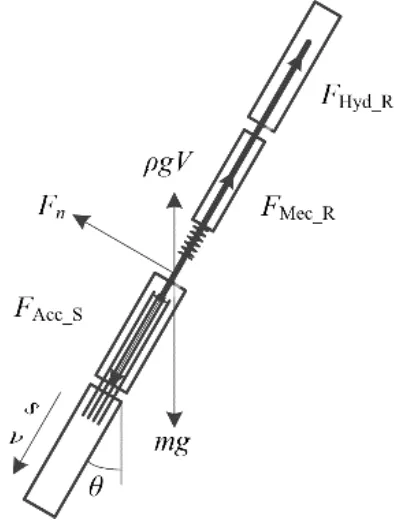
图2 ACP100S驱动线运动部件受力示意图Fig.2 Schematic diagram of forces on moving parts of ACP100S drive line
摇摆工况下主要多了离心力和科里奥利力。科里奥利力改变了导向结构对运动部件的正压力分布,影响机械阻力的大小。经归纳,建立驱动线运动部件的动力学方程如下:
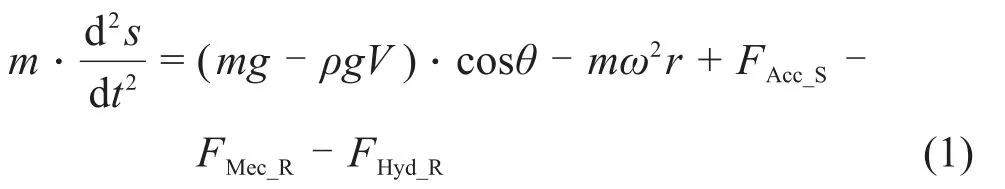
式中:m为运动部件总质量;s为运动部件位移;ρ为流体密度;V为运动部件总体积;FAcc_S为弹簧力;FMec_R为机械阻力;FHyd_R为水力阻力;ω为角速度;r为运动部件质心与摇摆中心之间的距离。ACP100S驱动线的摇摆中心取反应堆重心位置。
只考虑驱动线做单自由度摇摆运动,频率为f,摇摆角度为θm,初始倾角为θ0,则:
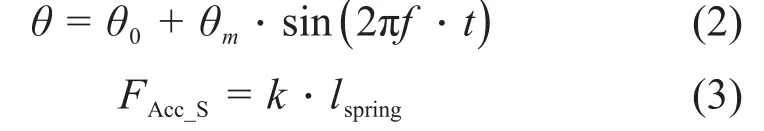
式中:k为弹簧刚度;lspring为弹簧的作用长度。
ACP100S为一体化反应堆,内置蒸汽发生器,反应堆较高,驱动杆细长,和控制棒一样具有很大的柔性,易变形。驱动杆和控制棒运动时与导向结构之间存在复杂的接触作用,如图3所示。
由此可知:
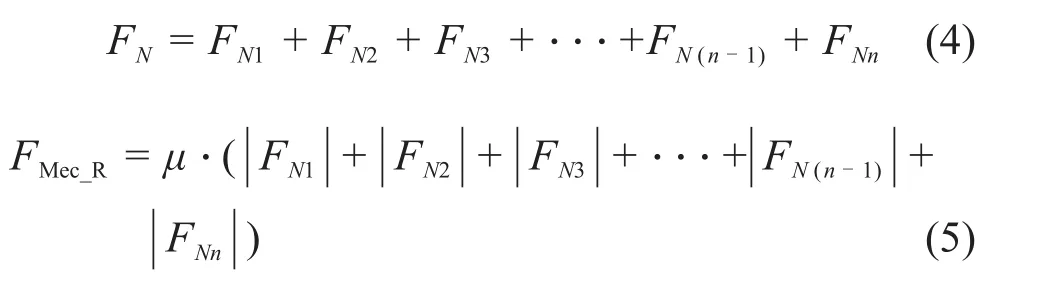
式中:μ为对应的动摩擦系数,可运用动力学仿真软件LMS Motion 13.8建立虚拟小球碰撞模型对其进行建模求解[7]。
驱动线落棒时运动部件所受的水阻力由三部分组成:物体加速运动产生的流体阻力FHa、粘性摩擦阻力FHf和压差阻力FHp。

图3 导向结构对运动部件的正压力Fig.3 Positive pressure of the guide structure on the moving parts
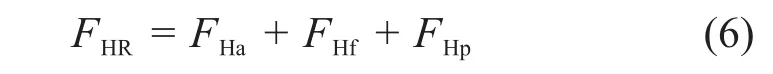
ACP100S驱动线可根据结构特点划分为三个流体域:驱动机构流体域、控制棒导向筒流体域和燃料组件流体域,流道形状分为圆管流道和环形流道两种。由于驱动杆保护管两端贯通,结构开放,与驱动杆之间间隙较大,对驱动线落棒影响忽略不计。
由文献[8]可知:
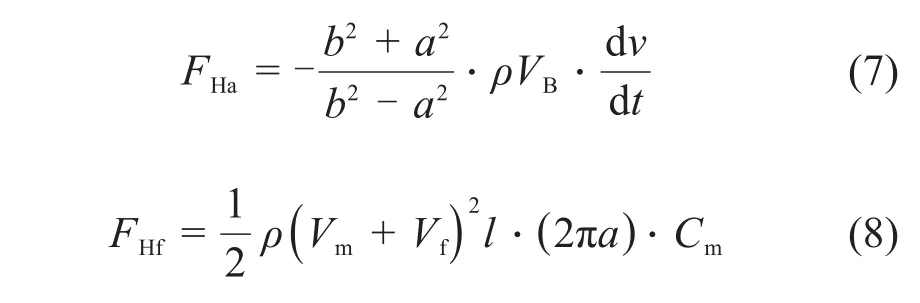
式中:a、l分别为驱动杆或控制棒半径和长度;b为导向管半径;VB为区域内运动部件的排水体积;Vm为运动部件的速度;Vf为流体的速度;Cm为导向管内表面的粘性摩擦系数,与流道尺寸和雷诺数有关。

式中:Δp为运动部件两端的流体压差;S为运动部件的等效横截面积。
2 驱动线落棒过程联合仿真
采用计算软件MATLAB R2012a和动力学仿真软件Motion联合,进行落棒过程仿真计算。根据前文所述的水力阻力计算理论,分别编写MATLAB子程序求解驱动机构、控制棒导向筒、燃料组件导向管内运动部件所受的水力阻力和弹簧力,再联合Motion中设置的驱动线接触碰撞模型,对ACP100S的落棒过程进行联合仿真,总流程图见图4。
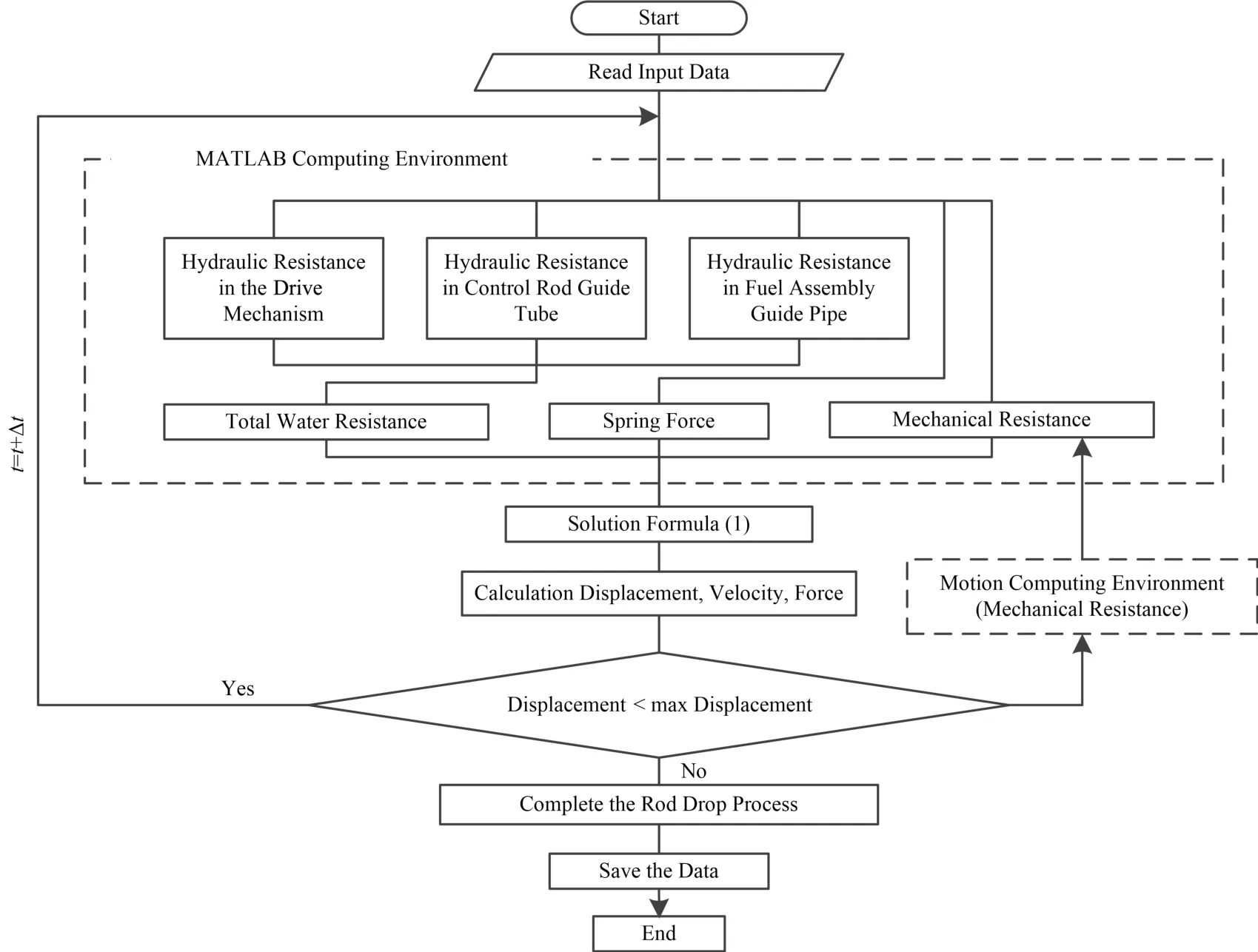
图4 联合仿真总流程图Fig.4 General flow chart of joint simulation
3 计算结果及分析
由于吨位大及靠近海岸线,正常运行时,ACP100S浮动平台摇摆的角度小、频率低,角速度ω很小,摇摆只对驱动线的可靠性以及驱动机构的耐磨性能有一定的影响,而对驱动线的落棒时间影响可以忽略不计,仿真计算时不予以考虑。因此,只进行两种状态共4种典型工况下全高度落棒的仿真计算:1)竖直静止状态,分有弹簧作用力(作用长度为1/4落棒行程)和无弹簧作用力两种工况;2)倾斜30°静止状态,分有弹簧作用力(作用长度为1/4落棒行程)和无弹簧作用力两种工况。此外,为了验证不同设计参数的弹簧对驱动线落棒的影响,仿真过程中对作用长度为1/2落棒行程的弹簧进行了对比计算(设定弹簧的刚度不变)。驱动线参数如表1所示。

表1 驱动线参数Table 1 Drive line parameters
3.1 落棒过程理论分析
驱动线落棒过程中受到机械摩擦力、浮力、重力、流体阻力、弹簧力的共同作用。由于流体阻力与落棒速度正相关,且控制棒在下落过程中驱动杆上端耐压壳内由于液体体积增加,造成了负压。因此控制棒在重力作用下做加速度逐渐减小的加速运动。另一方面,在控制棒插入燃料组件导向管过程中,不断将导向管中的流体压出底部端塞排水孔和导向管侧壁流水孔,以及沿着控制棒与导向管之间的环形空间流出导向管,控制棒与导向管之间的间隙大小决定了控制棒表面流体速度梯度大小,从而影响到控制棒上流体剪切力大小。尤其当控制棒下落到缓冲段时,由于流通截面积的瞬间变化,且导向管侧壁流水孔的阻塞造成导向管内产生巨大压差,控制棒阻力也相应变大。在这些阻力的共同作用下,控制棒运动速度会迅速减小,最终趋于平稳达到最低位置。
3.2 自由落棒工况
图5(a)、(b)分别给出了竖直-倾斜状态驱动线落棒速度、位移、水力阻力对比。不难看出,处于倾斜状态下的驱动线,由于下滑力的下降以及机械摩擦力的增加,导致控制棒落棒速度降低,控制棒也因此获得较小的水力阻力,但是由于水力阻力降低后,机械阻力成为影响落棒的主要因素,最终导致缓冲时间增大,快插时间均延长,总的落棒时间增加。这一点与一般驱动线试验结论一致,在较大倾斜角度下,控制棒时常会出现无法落到底部的情况。因此倾斜工况往往会导致驱动线落棒条件变得恶劣。
3.3 非能动加速工况
图6(a)、(b)给出了弹簧作用下驱动线落棒速度、位移、水力阻力对比。可以明显看到,在弹簧的作用下,在快插段,由于弹簧的作用,控制棒速度快速增加,并且在相同刚度下,弹簧的作用长度越长,控制棒的速度就越大,这也导致了水力阻力的迅速变大,但是综合作用下,控制棒落棒时间缩短,落棒性能得到改善。另外一方面,在较大倾斜角度下,控制棒由于机械阻力作用,几乎不可能运动,但是由于有弹簧的作用,可以克服机械摩擦保证控制棒仍能及时插入堆芯,保证反应堆安全。
此外,当控制棒进入缓冲段后,竖直、倾斜同种状态下控制棒的末速度基本一致,这主要是由于弹簧作用结束后,控制棒的受力情况与无弹簧作用的条件基本一致,重力最终会与水力阻力达到平衡,而水力阻力与控制棒速度又存在一定的对应的关系,因此导致控制棒进入缓冲段后,竖直、倾斜同种状态下控制棒的末速度基本一致。
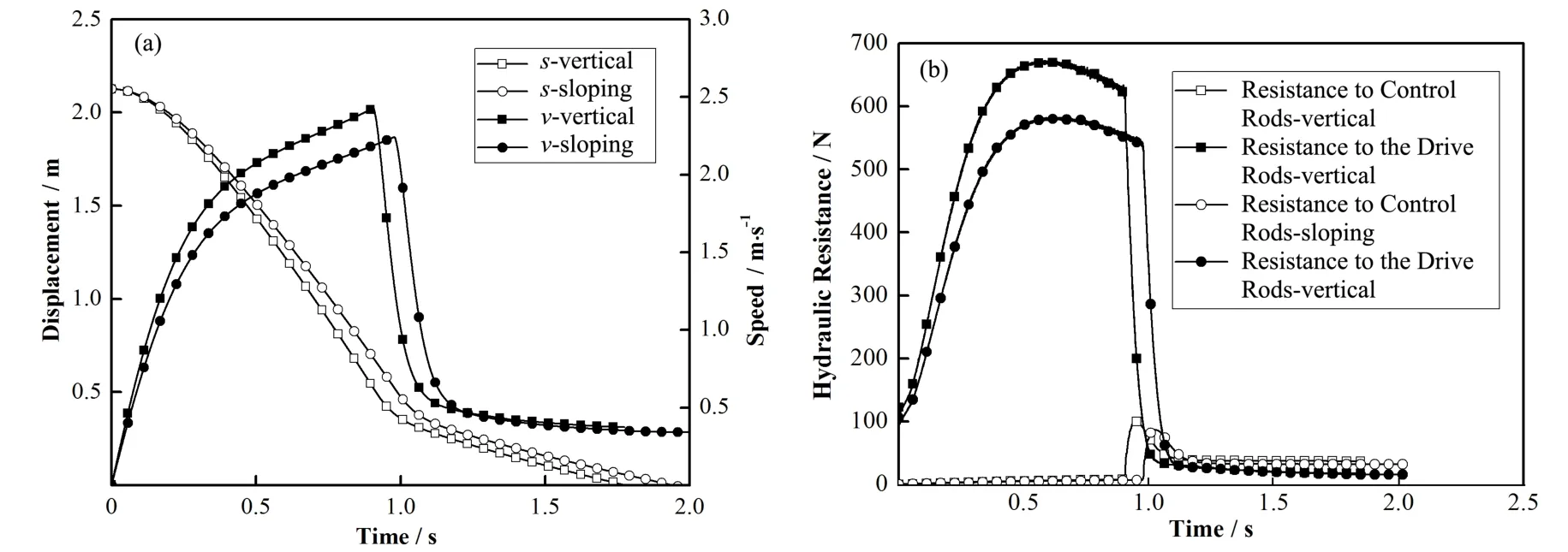
图5 竖直-倾斜状态驱动线落棒速度位移对比(a)和水力阻力对比(b)Fig.5 Comparison of velocity and displacement(a),and hydraulic resistance(b)of dropping rod of driving line in vertically-sloping state
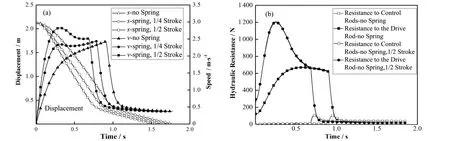
图6 弹簧作用下驱动线落棒速度位移对比(a)和水力阻力对比(b)Fig.6 Comparison of velocity displacement(a)and hydraulic resistance(b)of driving line under spring action
4 结语
本文建立了考虑非能动加速作用的ACP100S一体化反应堆驱动线仿真模型,并对ACP100S驱动线典型工况下的落棒行为进行了仿真研究,得到如下结论:
1)非能动加速措施的设置有利于驱动线克服海洋环境条件下控制棒落棒的不利因素,可以有效缩短落棒时间,确保堆芯安全。
2)当控制棒进入缓冲段后,竖直、倾斜同种状态下控制棒的末速度基本一致,这主要是由于弹簧作用结束后,控制棒的受力情况与无弹簧作用的条件基本一致,重力最终会与水力阻力达到平衡,而水力阻力与控制棒速度又存在一定的对应的关系。
