基于REVENT实验的气溶胶再夹带模型适用性分析
2020-07-20何丽雯侯丽强佟立丽曹学武
何丽雯 侯丽强 佟立丽 曹学武
1(上海交通大学机械与动力工程学院 上海 200240)
2(中国核动力研究设计院核反应堆系统设计技术重点实验室 成都 610041)
液相中气溶胶在蒸汽作用下被夹带回到气相中的现象称为再夹带[1]。核反应堆发生事故时裂变产物从堆芯释放,并以气态、蒸汽、气溶胶等形式存在,气溶胶是分散并悬浮在介质中的固体或液体小颗粒,是裂变产物的主要存在形式之一,其在安全壳内的行为直接影响最终释放到环境中的放射性源项。在核反应堆事故后卸压等特定场景下,安全壳内的液体大量蒸发,已经被冲洗掉的气溶胶粒子在再夹带作用下回到空气中,气相中放射性源项增加,并可能导致最终向环境的释放增加[2]。因此开展气溶胶再夹带行为研究,对澄清严重事故最终的释放源项具有重要意义。
在再夹带实验研究方面,1985~1987 年 Bunz[3]在REST装置上开展了空气-蒸汽混合气体条件下的气溶胶再夹带实验研究,且仅采用了不可溶性的BaSO4作为实验材料。1994年日本原子能研究所的Kudo等[4]模拟实际电场中卸压导致的再夹带过程开展了实验研究,但仅在实验容器内压力分别从1.3 MPa、1.5 MPa快速下降至环境压力条件下开展了实验研究,且两工况测量得到的气溶胶再夹带因子相差较大。1999年瑞士联邦理工学院的Cosandey[5]参考瑞士核电站(900 MW热功率)以1:20的缩放比建立了REVENT实验装置,并采用可溶性和不可溶性气溶胶在0.2~0.6 MPa压力、0%~36%空气份额条件下开展了再夹带实验研究。2003~2007年在 THAI(Thermal-hydraulics,Hydrogen,Aerosol,and Iodine)等试验装置中进行了气溶胶再夹带实验[6],但实验仅在较低的压力范围内进行。因此,选择覆盖的热工水力和源项参数范围较广且考虑影响因素较为全面的Revent实验作为气溶胶再夹带模型适用性评估的验证实验。
在模型研究方面,1996年Müller等[7-8]通过实验发现随着沸腾池中示踪剂浓度的增加,气溶胶的再夹带率也随之增加,并建立了基于在沸腾池周围一定空间内动量和能量守恒的气溶胶再夹带模型。1999年Cosandey[5]在Müller模型的基础上考虑自由对流等影响因素,提出了半经验模型。Kataoka等[9-10]根据与液面的距离将再夹带区间分为3部分:表面附近区域、动量控制区域和沉积控制区域,并针对不同区域提出了考虑不同影响因素的再夹带半经验公式。安全壳内气溶胶再夹带行为是国际上严重事故研究领域中的关键问题,但目前通用的严重事故分析程序中尚未考虑此行为[11],因此有必要开展气溶胶再夹带模型的适用性分析为后续向严重事故分析程序中添加提供支持。
本文中筛选出两个典型的再夹带模型:Kataoka&Ishi's模型和Cosandey's模型,分别针对Revent实验建立分析模型,通过对比分析模型模拟结果与实验测量值评估模型的适用性,并探究关键因素对再夹带的影响。
1 再夹带模型
沸腾水池中气溶胶在蒸汽夹带下克服重力作用重新进入气相的现象即为气溶胶再夹带,现有的气溶胶再夹带模型多为半经验公式,不同模型的区别主要在于对气流作用和重力影响的表征方法。
1.1 Kataoka&Ishi's模型
Kataoka&Ishi's模型[9]认为沸腾池上部不同区域影响再夹带的主要因素不同,按照距离液面由近到远可分为三个区域:表面附近区域、动量控制区域和沉积控制区域,再夹带区域在高度方向上的分布如图1所示。

图1 再夹带区域在高度方向上的分布Fig.1 The distribution of the reentrainment regions
表面附近区域仅限于池面附近,在这一区域所有脱离水池表面的液滴均会再夹带,此区域的上限为:

动量控制区域处于中间高度范围,再夹带与粒子的初始动量和沉降速度有关。动量控制区域的上限可以表示为:

在这个区域内,再夹带因子和与液面之间的距离成负相关。根据液体表面气流速度,可分为:由低速气流导致的再夹带,再夹带因子可表示为式(4)和由中速气流导致的再夹带,再夹带因子可表示为式(5)。

式中:k1为常数,k1=6.09×109。
低速气流的判断依据为:

在沉积控制区域,液滴的沉积是影响再夹带的主要因素。此区域中再夹带粒子的沉降速度低于气流速度,再夹带因子随着高度的升高而降低。

如果忽略沉积的影响,此区域再夹带因子与高度无关,可表示为:
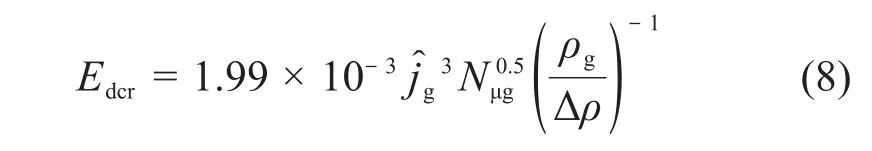
1.2 Cosandey's模型
Cosandey[5]考虑沸腾池浓度、惯性、表面张力、重力和自然对流的影响,结合无量纲特征参数,构建了气溶胶再夹带模型。可溶性气溶胶再夹带的浓度为:
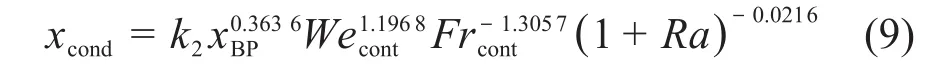
式中:k2为常数,k2=2.954 × 10-9。
不可溶性气溶胶再夹带的浓度为:

再夹带因子可表示为:

式中:xBP为沸腾水池中气溶胶浓度。Wecont=为韦伯数,表征惯性与表面张力的影为弗劳德数,表征惯性与重力的影响;Ra为瑞利数,表征自由对流的影响,Ra=为表面气流速度;Dcont为安全壳直径;ρl为液体密度;σ为表面张力;g为重力加速度;H为沸腾池表面到安全壳顶部之间的距离;β为体积膨胀系数;ΔT为水池与气相之间的温度差;ρhom为气相密度;μhom为气相的粘度;Pr为普朗特数。
2 模型适用性验证
Revent(Reentraiment by Venting)实验[5]由瑞士联邦理工大学开展,探究了沸腾池中气溶胶特性、压力、气体组分等对再夹带的影响。在容器底部的水池中安装有电加热器,模拟反应堆的衰变热;在实验容器顶部安装热交换器,使顶部与底部产生温度差,模拟实际情况中的自然对流;通过向水池中提供空气等模拟反应堆事故情况下金属和蒸汽反应或熔融的堆芯与混凝土反应产生的不可凝气体。实验中采用KI、CsI作为实验材料探究可溶性气溶胶再夹带行为,采用Al2O3为实验材料探究不可溶性气溶胶再夹带行为。
2.1 Kataoka&Ishi's模型适用性分析
利用Kataoka&Ishi's模型针对Revent实验中采用可溶性气溶胶作为实验材料的工况开展模拟研究,表1为不同压力、不同气体组分等典型工况下Kataoka&Ishi's模型模拟得到的各夹带区域的上限。实验容器中整个再夹带空间高度(液面距离容器顶部的距离)约为3 m,而表面附近区域的高度仅为微米量级,此区域的再夹带对整个空间内的再夹带影响较小,故在此处不予讨论。
模型计算的Revent实验动量控制区域上限为0.11~0.16 m,且实验在动量控制区域为低速气流,故依据式(4)模拟得到动量控制区域再夹带因子。表2为Kataoka&Ishi's模型预测结果与实验结果对比,预测的0.1 m高度处再夹带因子与实验测量再夹带因子拟合较好,不存在量级上的差异。图2和图3为针对Revent实验采用可溶性气溶胶的所有工况,Kataoka&Ishi's模型动量控制区域预测与实验测量再夹带因子对比。纯蒸汽条件下约有一半的工况模拟与实验误差超过100%,即在图中表示的误差带外,且大部分工况实验测量值高于模型模拟值。而对于空气-蒸汽条件,大部分的点落在了y=2x和y=0.5x所夹的区域内,即误差小于100%,整体来看模型预测值偏高。另一方面,无论是否考虑沉积影响,模型预测的沉积控制区域(2 m)再夹带因子与实验测量的整体区间内再夹带因子相比存在6~8个量级的差异。

表1 Kataoka&Ishi's模型模拟各夹带区域上限Table 1 The predicted upper limit of reentrainment regions of Kataoka&Ishi's model

图2 动量控制区域Kataoka&Ishi's模型模拟(纯蒸汽)Fig.2 Comparison between the prediction results of Kataoka&Ishi's model in the momentum controlled region and the experimental results(steam)
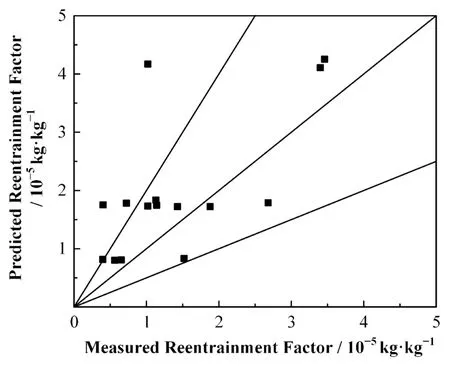
图3 动量控制区域Kataoka&Ishi's模型模拟(空气-蒸汽)Fig.3 Comparison between the prediction results of Kataoka&Ishi's model in the momentum controlled region and the experimental results(air-steam)

表2 Kataoka&Ishi's模型模拟结果与实验结果对比Table 2 Comparison between the prediction results of Kataoka&Ishi's model and the experimental measurements
气溶胶行为模拟具有较大的不确定性,水洗效率预测为实验值的0.1~10倍均为可接受范围[12],部分通用的分析程序对气溶胶沉降行为的预测误差超过100%[13],对气溶胶再悬浮行为的预测误差超过200%[13]。故认为 Kataoka&Ishi's模型预测的动量控制区域再夹带因子与实验测量值拟合较好,但沉积控制区域预测值明显偏低,且对于空气-蒸汽混合条件下的预测结果优于纯蒸汽条件下的预测结果。但Kataoka&Ishi's模型并未考虑沸腾水池中气溶胶浓度对再夹带行为的影响,只适用于模拟可溶性气溶胶的再夹带行为。
2.2 Cosandey's模型适用性分析
利用Cosandey's模型针对Revent实验开展模拟研究,图4、5为采用可溶性气溶胶作为实验材料,Cosandey's模型预测值与实验测量结果对比,纯蒸汽条件下27个工况中仅1个工况模拟误差超过100%,空气-蒸汽混合气体条件下大部分的点也处于y=2x和y=0.5x所夹区域内。图6和图7为采用不可溶性气溶胶作为实验材料,纯蒸汽条件和空气-蒸汽混合气体条件下Cosandey's模型模拟与实验测量结果对比,整体来看模型预测值与实验测量值拟合较好,但针对再夹带因子较小工况的模型预测值略有偏高。
通过对比分析Cosandey's模型针对Revent实验不同工况的模拟结果与实验测量值,认为模型可适用于可溶性气溶胶、不可溶性气溶胶在纯蒸汽、空气-蒸汽混合条件下的再夹带行为模拟,且对于纯蒸汽条件下的预测结果优于空气-蒸汽混合条件下的预测结果。

图4 Cosandey's模型模拟与实验结果对比(可溶性-纯蒸汽)Fig.4 Comparison between the prediction results of Cosandey's model and the experimental results(soluble-steam)

图5 Cosandey's模型模拟与实验结果对比(可溶性-空气-蒸汽)Fig.5 Comparison between the prediction results of Cosandey's model and the experimental results(soluble-airsteam)
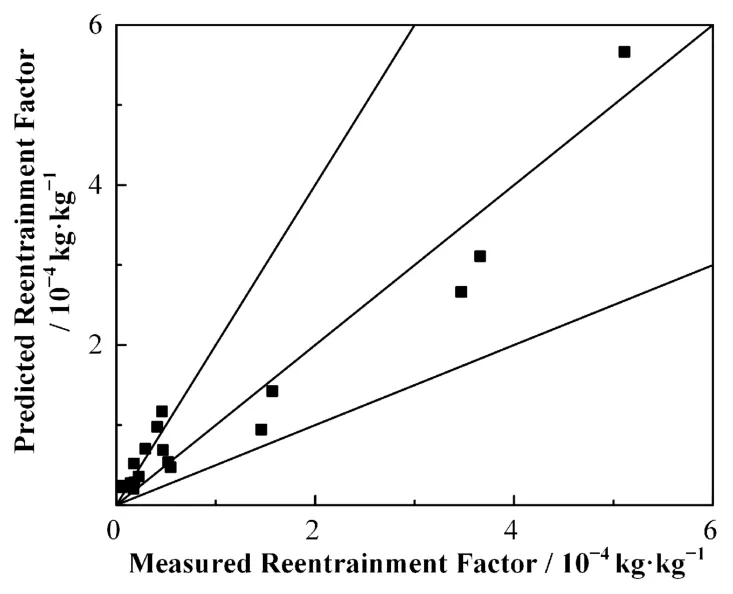
图6 Cosandey's模型模拟与实验结果对比(不可溶性气溶胶-纯蒸汽)Fig.6 Comparison between the prediction results of Cosandey's model and the experimental results(solid-steam)

图7 Cosandey's模型模拟与实验结果对比(不可溶性气溶胶-空气-蒸汽)Fig.7 Comparison between the prediction results of Cosandey's model and the experimental results(solid-air-steam)
3 结语
通过对比分析Revent实验测量结果与Kataoka&Ishi's模型、Cosandey's模型模拟值,评估了模型预测气溶胶再夹带行为的适用性,分析了气溶胶特性、气体组分等条件对再夹带预测的影响。
结果表明:Kataoka&Ishi's模型预测的动量控制区域再夹带因子与实验测量值拟合较好,但沉积控制区域预测值明显偏低,且对于空气-蒸汽混合条件下的预测结果优于纯蒸汽条件下的预测结果,但该模型仅适用于可溶性气溶胶。Cosandey's模型可适用于可溶性气溶胶、不可溶性气溶胶在纯蒸汽、空气-蒸汽混合条件下的再夹带行为模拟,且对于纯蒸汽条件下的预测结果优于空气-蒸汽混合条件下的预测结果。建议使用Cosandey's模型预测核电厂事故工况下安全壳内不同种类气溶胶粒子再夹带行为。
