生存资料回归模型分析——Cox比例风险假设的图形检验法

宋德胜 ，李长平 ，2，刘媛媛 ，崔 壮 *，胡良平

（1.天津医科大学公共卫生学院流行病与卫生统计学教研室，天津 300070；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3.军事科学院研究生院，北京 100850*通信作者：崔 壮，E-mail：cuizhuang@tmu.edu.cn）

在临床实践中，调查者会在指定的时间段内随访研究对象直到其发生预先指定的观察事件。然而，部分研究对象会在随访期间出于某种原因而退出研究，例如，出现非观察事件导致的死亡或者研究对象主动要求退出等。这些提前退出随访的情况被称之为截尾。这种截尾会导致收集的数据不完整。因此，传统的参数回归模型并不适用于处理生存资料。目前，生存分析中最常用的回归模型是英国统计学家D.R.Cox于1972年提出的Cox半参数回归模型。该模型不要求生存时间满足特定的概率分布，但要求生存资料满足比例风险假定。

1 比例风险概念

经典的Cox比例风险回归模型存在一个假设：不论基线风险如何，在基线以后的任何时间点上，分别在影响因素的“暴露水平”与“非暴露水平”条件下的发生事件的风险比是恒定的，换言之，所考察的影响因素对于所考察事件的效应不会随时间而改变。这就是比例风险恒定假设［1］，简称为PH假设。例如，年龄为50岁时，男性发生心脏病的风险是女性的2倍，那么60岁时，男性的风险仍然是女性的2倍（说明：此例中的“影响因素”为“性别”，其“暴露水平”为“男性”，“非暴露水平”为“女性”）。但有很多临床生存资料并不满足此假设，此时，这种变量（即影响因素）效应的风险称为非比例风险。这种效应随时间变化的变量称为时间依赖型变量，即时依协变量［2］。比例风险恒定更普遍的情形是：设Xi为第i位受试对象的自变量向量、Xj为第j位受试对象的自变量向量，PH假设为第i位受试对象与第j位受试对象风险之比仅与他们的自变量向量的取值之差呈比例关系，而与自变量向量在什么时间点取值无关。

2 使用图示法检验比例风险假定

判断比例风险假设是否成立的一个简单的方法是图示法，即通过观察每一个定性自变量各水平条件下的Kaplan-Meier生存曲线图是否存在交叉，如果存在交叉，则表示该定性自变量不满足比例风险假设。另外，对于特定的定性自变量的各水平组，绘制ln｛-ln［S（t）］｝与生存时间或生存时间的对数的关系图，如果线段明显不平行，说明该定性自变量不符合比例风险假设。对于连续型自变量，可使用Schoenfeld残差图、Score残差图进行判断，也可以将连续型自变量定性化，然后采取前述的图示法。

对于已经观测到的事件时间，假如已知第i个对象的第k个协变量及其取值，则Schoenfeld残差见式（1）［3］：

式（1）中，Xik是第i个对象第k个协变量的值，wik是给定事件时间的风险集中协变量值的加权均数。若Schoenfeld残差值为正，表示在对应的死亡时间点，X的实际值高于预期值。绘制Schoenfeld残差与生存时间的广义线性回归图，若图形呈现非零斜率，表示该变量不满足比例风险假设。

Martingale残差定义见式（2）［4］：

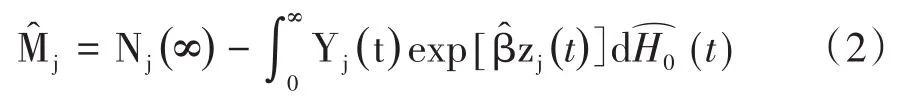
式（2）中，Nj（t）代表t时刻个体j是否经历了某事件的指示变量，Yj(t)是t时刻前个体j是否在观察中的指示变量，是回归系数向量，zj(t)是t时刻，第j个个体的协变量向量，是累积基准风险函数的Breslow估计。因此，Martingale残差可能具有超额事件数，并且这些残差的总和等于0。在满足比例风险假设的前提下，如果利用该残差与时间作图，则可以观察到该残差随时间围绕一条水平线波动。

通过SAS的PHREG过程中ASSESS语句绘制累积得分残差与时间的图形以检验比例风险假设。图形中每条曲线的值开始于0且终止于0，这是一种Brownian过程。在比例风险的假设下，该选项产生若干随机路径。将随机产生的路径与实际数据相对比，若变量的实际路径在随机路径范围内，则表示该协变量服从比例风险假设。反之，则不服从比例风险假设。但是，非比例风险假设的形式则不清楚。

3 SAS软件实现

3.1 创建数据集

Krall等［5］对一项多发性骨髓瘤研究的数据进行了分析。65例患者接受了烷化剂治疗，其中48例在研究期间去世，17例存活。创建的数据集Myeloma包含变量如下：Time（预后生存时间）；Vstatus（患者状态，0表示存活，1表示死亡）；在诊断时被认为与生存时间有关的变量，如LogBUN（血尿素氮水平）；HGB（血红蛋白水平）；Platelet（血小板水平，0表示非正常，1表示正常）；Age（年龄）；LogWBC（白细胞水平的对数）；Frac（骨折，0表示未发生，1表示发生）；LogPBM（骨髓浆细胞对数百分比）；Protein（蛋白质水平）；Scalc（血钙水平）。

数据集创建程序如下：

3.2 比例风险假设检验

3.2.1 Kaplan-Meier生存曲线以及生存函数负对数的对数与时间的对数关系图

以下SAS语句使用图示法中的Kaplan-Meier生存曲线以及生存函数负对数的对数与时间的对数关系图判断定性变量是否符合比例风险假设。

【程序说明】ODS语句指定后续PROC LIFETEST产生的图形使用HTML BLUECML的样式显示，图形的DPI设置为300。PROC LIFETEST语句中，PLOTS选项的survival以及lls要求绘制Kaplan-Meier生存曲线与生存函数负对数的对数与时间的对数关系图。TIME语句指定生存时间与截尾指示变量（0表示截尾），STRATA语句指定需要考察是否满足PH假定的定性变量。

图1 不同PLATELET水平下的生存曲线

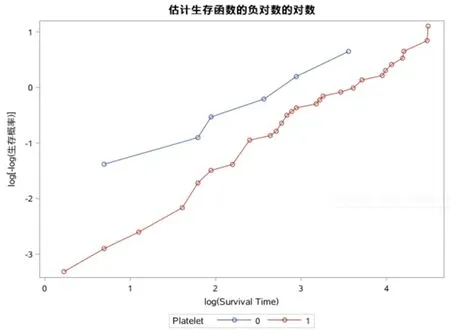
图2 不同PLATELET水平下的LOG［-LOG（生存函数）］与LOG（time）的变化趋势

图3 不同FRAC水平下的生存曲线

图4 不同FRAC水平下的LOG［-LOG（生存函数）］与LOG（time）的变化趋势

图1显示的是不同platelet水平下的生存曲线；图2显示的是不同platelet水平下的LOG［-LOG（生存函数）］与LOG（time）之间的折线图；图3显示的是不同FRAC水平下的生存曲线；图4显示的是不同FRAC水平下的LOG［-LOG（生存函数）］与LOG（time）之间的折线图。图1中，两条生存曲线无交叉；图2中，两条线没有明显交叉的趋势，因此可认为变量PLATELET满足比例风险假设；图3中，两条生存曲线存在交叉情况；图4中，两条曲线亦存在相交，因此可以认为FRAC不满足比例风险假设。

3.2.2 Schoenfeld残差与log（time）的关系图

SAS程序如下：

【程序说明】Proc phreg调用PHREG过程进行分析，data选项指定要分析的数据集是myeloma，zph选项（注意：此选项在SAS 9.3中无效）要求进行比例风险检验，括号中的notest表示不进行相关检验，fit指定是否呈现光滑曲线拟合结果，本例中使用了Spline，要求进行惩罚B样条曲线拟合。Class语句指定分类变量为platelet和frac。Model语句进行模型构建。Time*vstatus（0）中的time表示生存时间，当vstatus=0时代表截尾。等号右边为一系列自变量。Selection=s表示进行逐步选择筛选变量。

输出结果见表1、图5、图6。

表1 基于最大似然法估计回归参数

图5 变量logBun的缩放Schoenfeld残差与时间对数的关系图

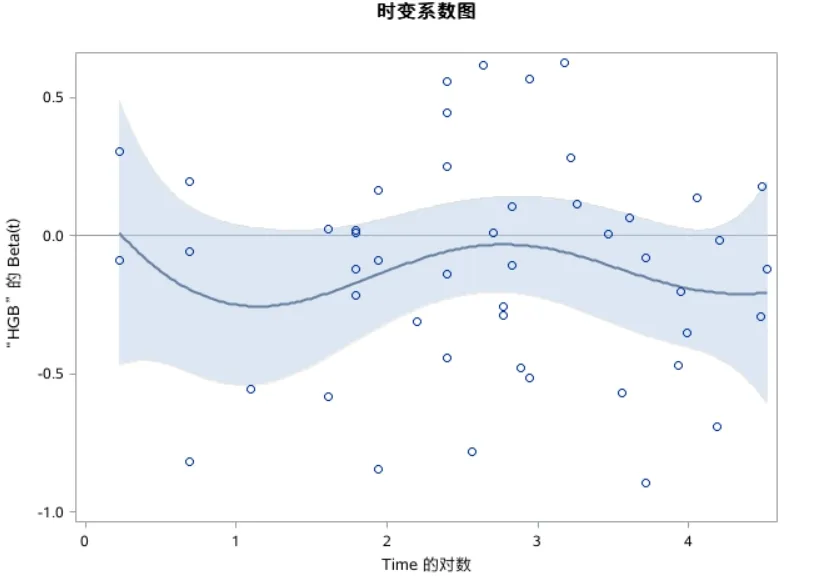
图6 变量HGB的缩放Schoenfeld残差与时间对数的关系图

【结果解释】最大似然估计结果显示，逐步回归筛选后，模型中剩余的变量为logBun和HGB。从这两个自变量的缩放Schoenfeld残差与时间对数的关系图可以看出，logBun拟合的曲线斜率明显不为0，而HGB拟合的曲线斜率基本为0。因此，LogBun不符合比例风险假设，HGB符合比例风险假设。

3.2.3 使用PHREG过程ASSESS语句判断比例风险假设是否成立

SAS程序如下：

【程序说明】ASSESS语句要求进行Cox回归模型的充分性检验。通过这个语句，可检验一个或多个协变量的函数形式。PH选项要求进行比例风险假设。Seed选项设置了种子数，以保证结果的重现性。对于用户指定的每个协变量［通过VAR=（变量列表）指定］，ASSESS语句会绘制已观测的累积Martingale残差与解释变量值的关系图，并模拟若干残差图形（通过NAPTHS=n指定）。

输出结果见图7、图8。

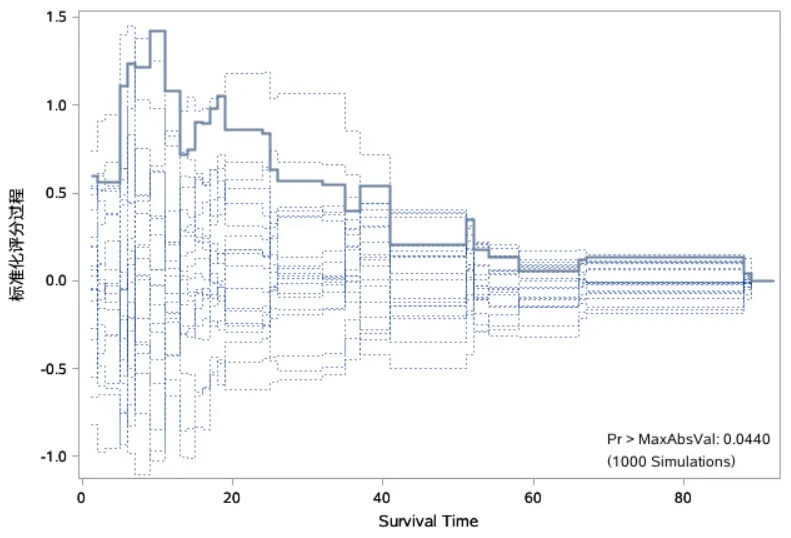
图7 变量LogBun的模拟路径图

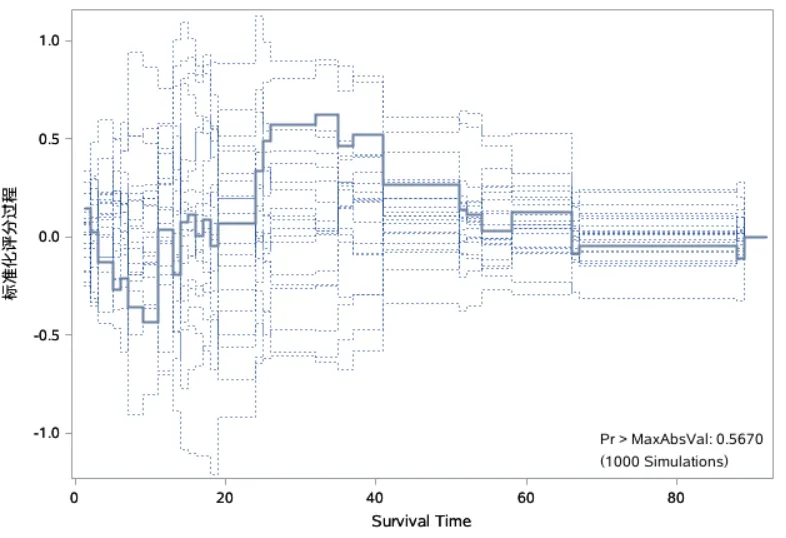
图8 变量HGB的模拟路径图

【结果解释】LogBun变量的实际路径在模拟路径外，而HGB变量的实际路径均在模拟路径范围内；模拟路径图右下角Kolmogorov-type supremum检验结果显示LogBun的P＜0.05。因此，LogBun不满足比例风险假设；而HGB变量满足比例风险假设。

4 小结

Cox比例风险回归模型常用于分析生存数据，需满足比例风险假设，但这在实际的生存资料中往往不能满足。因此，本文介绍了在临床试验中简便的比例风险假设的检验方法，即图示法。Kaplan-Meier生存曲线图和LLS生存函数负对数的对数与时间对数的关系图是最常用的用于直观判断分类变量是否满足比例风险假设的工具；对于定量变量，通过观察Schoenfeld残差与时间函数的关系图，可大致判断定量变量是否满足比例风险假设。另外，本文也使用了SAS程序PHREG过程ASSESS语句中的PH选项和RESAMPLE选项检验比例风险假设是否成立。