185/60R15 84H轮胎充气压力与负荷的函数关系研究

王志勇，罗 哲，刘昌波，张彦军，于国鸿，曲家玉

[浦林成山（山东）轮胎有限公司，山东 威海 264300]

通常认为轮胎的垂直负荷一部分由胎体承担，另一部分由充气压力承担[1]。随着轮胎充气压力的降低，胎体承受的负荷增大[1]。充气压力较低时，轮胎充气压力与负荷呈非线性关系，主要受轮胎自身材料性能影响；充气压力为零时，轮胎的负荷能力全部由轮胎自身材料的强度决定。本研究将185/60R15 84H轮胎的充气压力分为两个区间，分别使用软件拟合出标准下沉量（25.124 mm）下充气压力与负荷之间的函数关系，为轮胎充气压力与负荷的函数关系研究提供新的思路。

1 轮胎分析

在标准下沉量下，轮胎的充气压力与负荷不完全呈线性关系，当充气压力大于某值时，充气压力与负荷呈线性关系；当充气压力小于该值时，充气压力与负荷呈非线性关系[2]，如图1所示。由图1可见，在低充气压力下，轮胎充气压力与负荷的关系比较复杂。

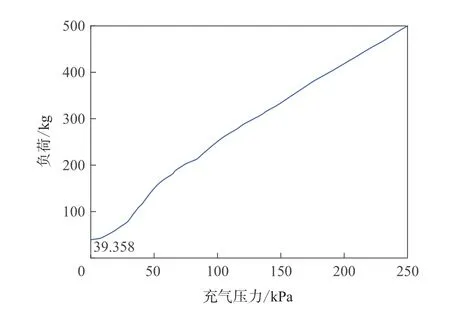
图1 标准下沉量（25.124 mm）下185/60R15 84H轮胎充气压力与负荷的关系曲线

试验轮胎为185/60R15 84H标准型无内胎轮胎，其骨架材料分析结果[3-4]如下：胎体结构 1层反包；胎体帘线材料-密度 聚酯1440dtex/2-28EPI；胎体帘线直径 0.61 mm；胎体帘线角度90°；冠带层缠绕结构 胎冠部位1层，胎肩部位2层（第2层宽度约为30 mm）；冠带层材料-密度 锦纶66-26EPI；冠带层宽度 164 mm；冠带层帘线直径 0.53 mm；冠带层角度 0°；带束层材料-密度钢丝帘线2×0.30ST-20EPI；2层带束层宽度146/136 mm；带束层角度 22°；钢丝圈排列结构六角形4-5-4；钢丝圈单丝直径 1.2 mm；三角胶高度 25 mm。

采用莱州华银实验仪器有限公司的LX-A型邵氏橡胶硬度计测试轮胎主要胶料部件的硬度。每次测量均在同种胶料部件的不同位置选测3点，取其算术平均值（保留到个位数）[3]。邵尔A型硬度（度）测试结果如下：胎面胶 70，胎侧胶 61，三角胶 85，胎圈胶 72。

2 轮胎充气压力与负荷的函数关系研究

观察图1中曲线变化趋势发现，当充气压力低于120 kPa时，函数曲线呈非线性关系；当充气压力高于120 kPa时，函数曲线趋向线性关系。因此，将充气压力分为0～120和120～250 kPa两个区间，即将图1所示试验数据分为两部分，分别拟合计算两个区间内轮胎充气压力与负荷的函数关系。

2.1 充气压力为0～120 kPa时函数关系拟合计算

用软件对充气压力为0～120 kPa区间内所有的充气压力与负荷的数据组进行拟合计算，以选出最优的函数表达式。

2.1.1 高斯函数

采用高斯函数进行拟合计算，得出函数表达式如下：

高斯函数拟合曲线如图2所示，图中箭头标注处为拟合曲线中出现偏差较大的位置（下同），拟合方差（R2）＝0.999 2。由图2可见，拟合曲线中有两处出现较大偏差，拟合效果不太理想。

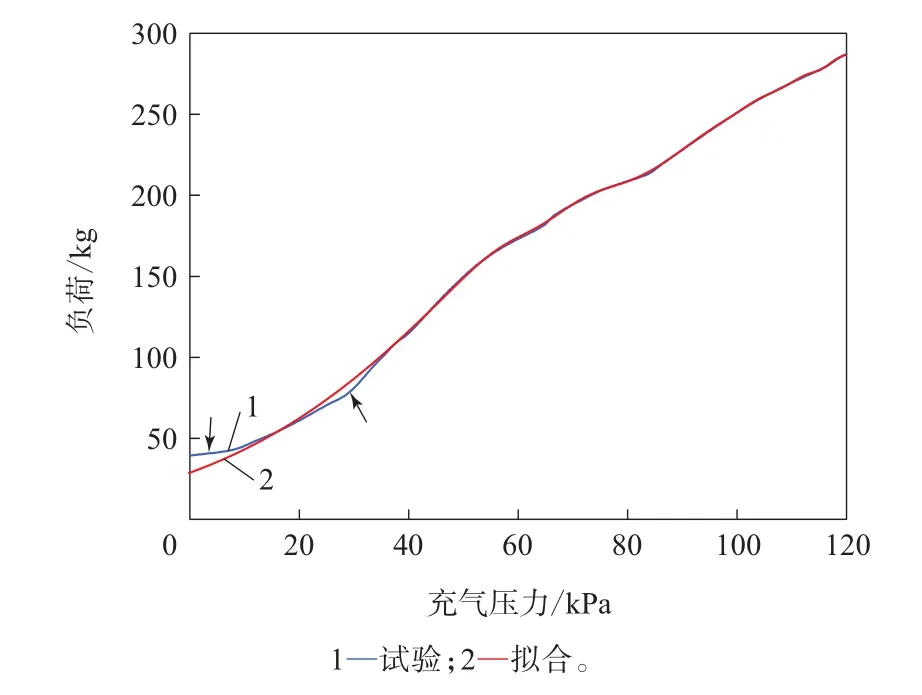
图2 高斯函数拟合充气压力与负荷的函数关系曲线

2.1.2 多项式函数

采用多项式函数进行拟合计算，得出函数表达式如下：

多项式函数拟合曲线如图3所示，R2＝0.999 8。由图3可见，拟合曲线中有两处出现轻微偏差，拟合效果比高斯函数好一些。

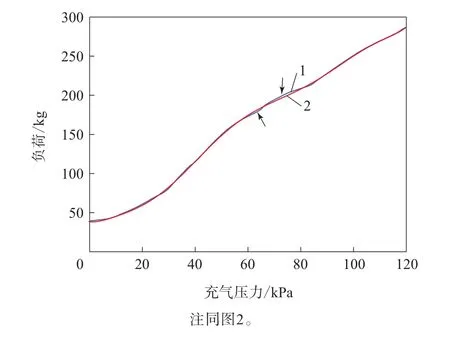
图3 多项式函数拟合充气压力与负荷的函数关系曲线

2.1.3 傅里叶函数

采用傅里叶函数进行拟合计算，得出函数表达式如下：

傅里叶函数拟合曲线如图4所示，R2＝1。由图4可见，拟合曲线未出现偏差，拟合效果良好。

图4 傅里叶函数拟合充气压力与负荷的函数关系曲线

2.2 充 气压力为120～250 kPa时函数关系拟合计算

由图1可见，充气压力为120～250 kPa时，充气压力与负荷明显呈线性关系，因此采用线性函数进行曲线拟合，得出函数表达式如下：

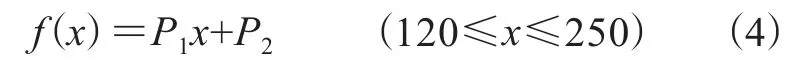
其中，系数P1＝1.65，P2＝88.23。

线性函数拟合曲线如图5所示，R2＝1。由图5可见，拟合曲线基本未出现偏差，拟合效果良好。

图5 线性函数拟合充气压力与负荷的函数关系曲线

3 结论

采用185/60R15 84H标准型轮胎研究充气压力与负荷之间的函数关系。结果表明，在标准下沉量下，当充气压力为0～120 kPa时，充气压力与负荷的函数关系宜采用傅里叶函数表征，而当充气压力为120～250 kPa时则采用线性函数表征。

本工作将充气压力分为两个区间进行分析，其他轮胎也可分为不同区间进行函数关系研究。本方法既可为轮胎充气压力与负荷的函数关系研究提供新的思路，也可为轮胎充气压力检测系统和有限元静负荷分析等提供参考。