基于双模谐振器的对称零点滤波器设计*

罗 兵

（广东机电职业技术学院 电子与通信学院，广东 广州 510515）

0 引言

微波滤波器是无线通信系统中不可缺少的组成部分，性能优良的微波滤波器能起到频带和信道选择的作用，且能滤除谐波，抑制杂散。因此，微波滤波器一直是无线通信系统领域的研究热点[1-10]。但是，随着无线通信的发展，迫于实际工程应用的需要，对滤波器的体积要求越来越高，小型化成为滤波器的必然发展方向。传统的单模滤波器尺寸大、性能差，随着移动通信技术的高集成度，滤波器的体积将越来越小。多模滤波器利用谐振器中对于不同的场分布有无穷多个谐振模式和谐振频率，其中具有相同谐振频率的模式称为简并模[2-3]。通常情况下，可以在单个谐振器中加入一些微扰（如开槽、切角或加入小的金属贴片、内切角等），以改变原正交简并模的电场分布，使得一对正交简并模之间发生耦合。两个耦合简并模的作用相当于两个耦合谐振器，从而在保持谐振回路不变的情况下，使谐振器的个数呈几何级数减少。因此，研究多模谐振器及其滤波器变得极其重要。

1 介质多模谐振器的设计

1.1 谐振器及其谐振频率的理论分析

在一个谐振腔中可能存在多个谐振模式，可以利用一个腔内的多个谐振模式设计谐振频率相同的多模耦合电路。一个谐振腔可以代替多个腔使用，因此可以起到缩小滤波器的整体尺寸、减轻重量的作用。关于双重及多重简并滤波器的实验模型已有大量的研究，获得了一定的滤波特性[3-4]。大多数文献所采用的是圆柱形、球面和正三角形谐振腔。各种形状的谐振器有其自身的特点，通常谐振器的形状决定了谐振器的谐振模式。为了谐振模式的需要，本文采用的谐振腔为圆柱形介质谐振块。图1为典型的介质谐振器结构。介质谐振器由具有高介电常数的圆柱形介质材料和安装在金属屏蔽腔的低介电常数的支撑柱构成。一般来说，金属屏蔽腔的大小需要确保其中模式频率以渐消逝模式工作。

图1 介质谐振器结构

对于介质圆柱形谐振器，谐振器频率的计算可以运用数值电磁法，采用麦克斯韦方程精确求解，也可以使用混合壁法或开波导法来计算。常见的两种计算方法如下。

（1）孤立的介质谐振器。电磁环境比较简单，其谐振频率通常利用式（1）来计算。

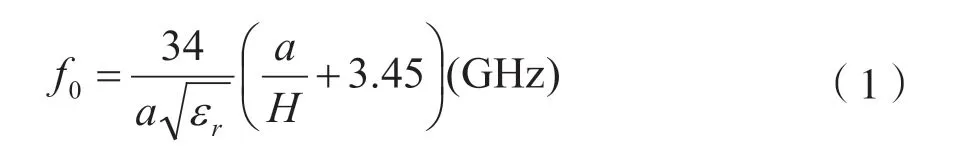
（2）微波电路中的介质谐振器。在微波电路中，电磁环境较复杂，使用开波导法分析。介质谐振器电路图如图2 所示，谐振器金属板内的区域被分为6 个区，1、2、3、4 区域有电磁场分布，5、6 区域中存在微弱电磁场，可以忽略不计，视为零场。

图2 介质谐振器电路

在介质谐振器内存在TE 波和TM 波。以TE 波为例（TM 波可以用类似方法分析），图2 中各区域中不随δ变化的HZ磁场分量通过求解赫姆霍兹方程获得：

其中，A1、A2、A3、A4、φ都是常量，同时：

如果HZ分量已知，则其余场的分量可以求出：

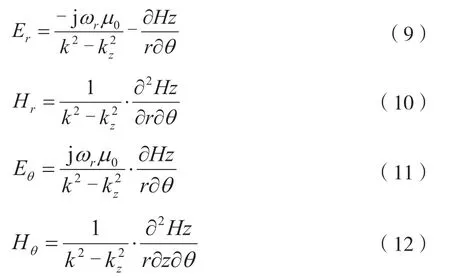
式中的K为所在区域的波数，在区域1 和4 时传播常数为β，在2 和3 区域时传播常数为jαi(i=1,2)。与θ无关的TE 模式，它们的Ez1、Er、Hθ为零。由于Hz在谐振器的界面上是连续的，所以式（2）～式（5）可以写为：

同理，Hr、Eθ为：

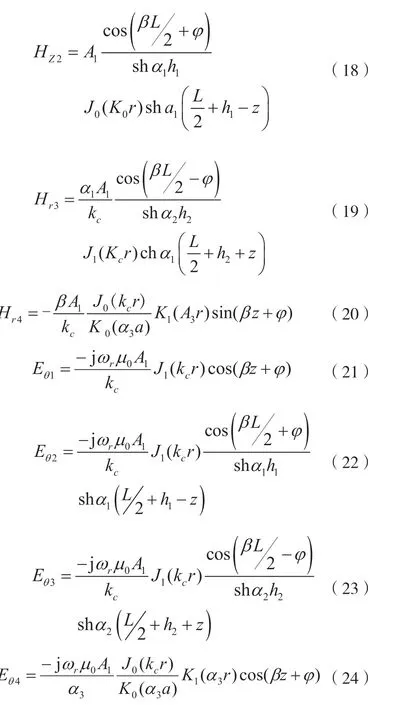
式中，J0(x)和J1(x)第一类贝塞尔函数，K0(x)与K1(x)为修正第二类贝塞尔函数。在边界上，由电场的边界条件Eθ1=Eθ4,可得：

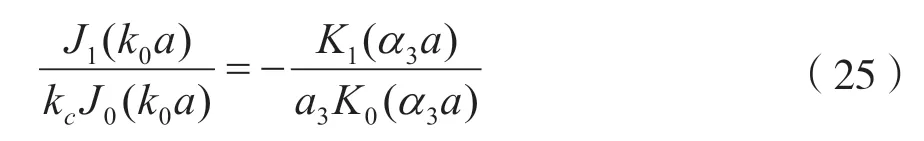
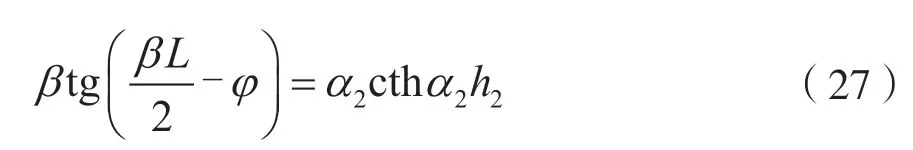
由式（26）和式（27），可得：

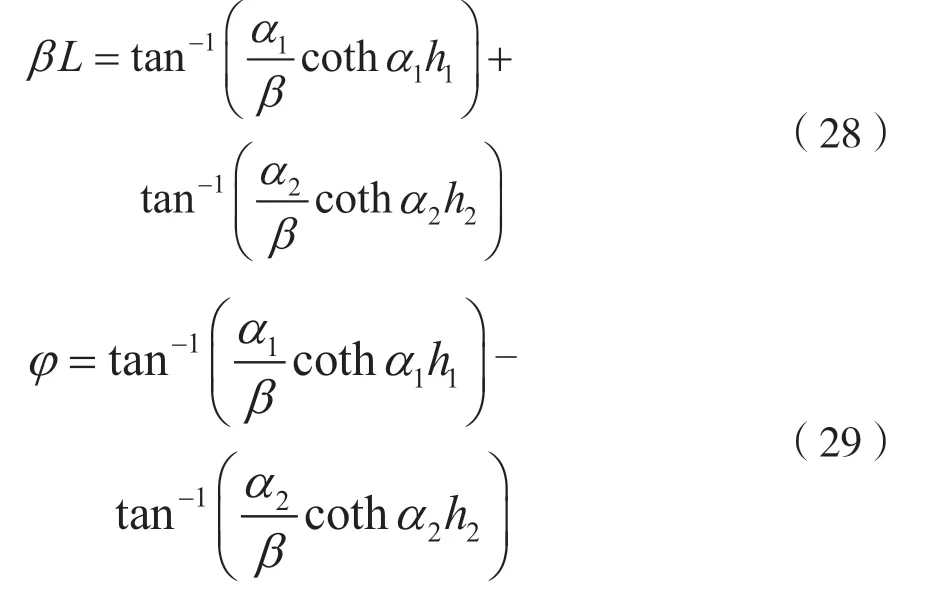
式（27）有许多离散的根，按大小排列后，k01为最小的根，所以与θ无关的模中，最低次模即主模是TE01δ模。

以上圆柱形介质谐振器谐振频率的精确数值计算方法要求解大量的数学方程，不但繁琐，而且耗时长。经过近年来的不断研究，也出现了一些近似的设计公式。随着IT 技术的发展，使用计算机仿真成为一种主流方式，而经验公式仅作为辅助设计。

1.2 谐振器的仿真设计

实际谐振器设计中，选取一种磁导率μ=1、介电常数εr=24 的介质材料。根据理论所述，初步将腔体大小设置为28mm×30mm×30mm，腔体材料镀银。利用HFSS（High Frequency Structure Simulator）软件初步构建介质谐振器的模型，如图3 所示，其中圆柱形介质谐振器的直径为23mm、高为9mm。设置HFSS 为本征模仿真，并计算8 个模式。经过仿真分析，最终得到介质谐振器的谐振频率和Q值结果，如图4 所示。

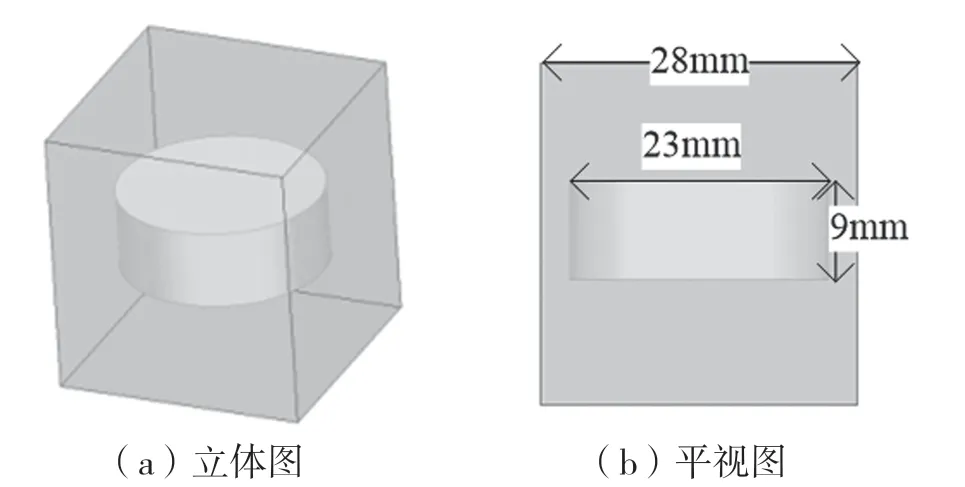
图3 介质谐振器模型

为了进一步对该谐振器的特性进行进一步的分析，使用HFSS对谐振器的前3个模式进行电场分析，分析结果如图5、图6 和图7 所示。

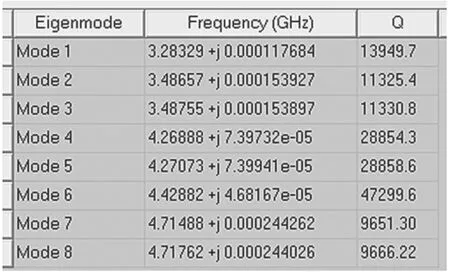
图4 本征模仿真结果

图5 TE01δ 模式的电场

图6 HEE11 简并双模沿径向顺时针45°极化模式的电场

图7 HEE11 简并双模沿径向逆时针45°极化模式的电场

由电场图可以看出，TE01δ模式的电场是圆对称的，属于环绕场，且大部分能量集中在介质谐振器的中间区域。HEE11 双模的电场从侧视图看是环绕场，能量集中在圆柱谐振器中部。

在圆柱形介质谐振腔体中，影响各个模式谐振频率的参数主要是介质谐振器的直径D和厚度H。图8、图9 分别是介质谐振器中主要的8 个模式的谐振频率与直径D和厚度H的关系图。

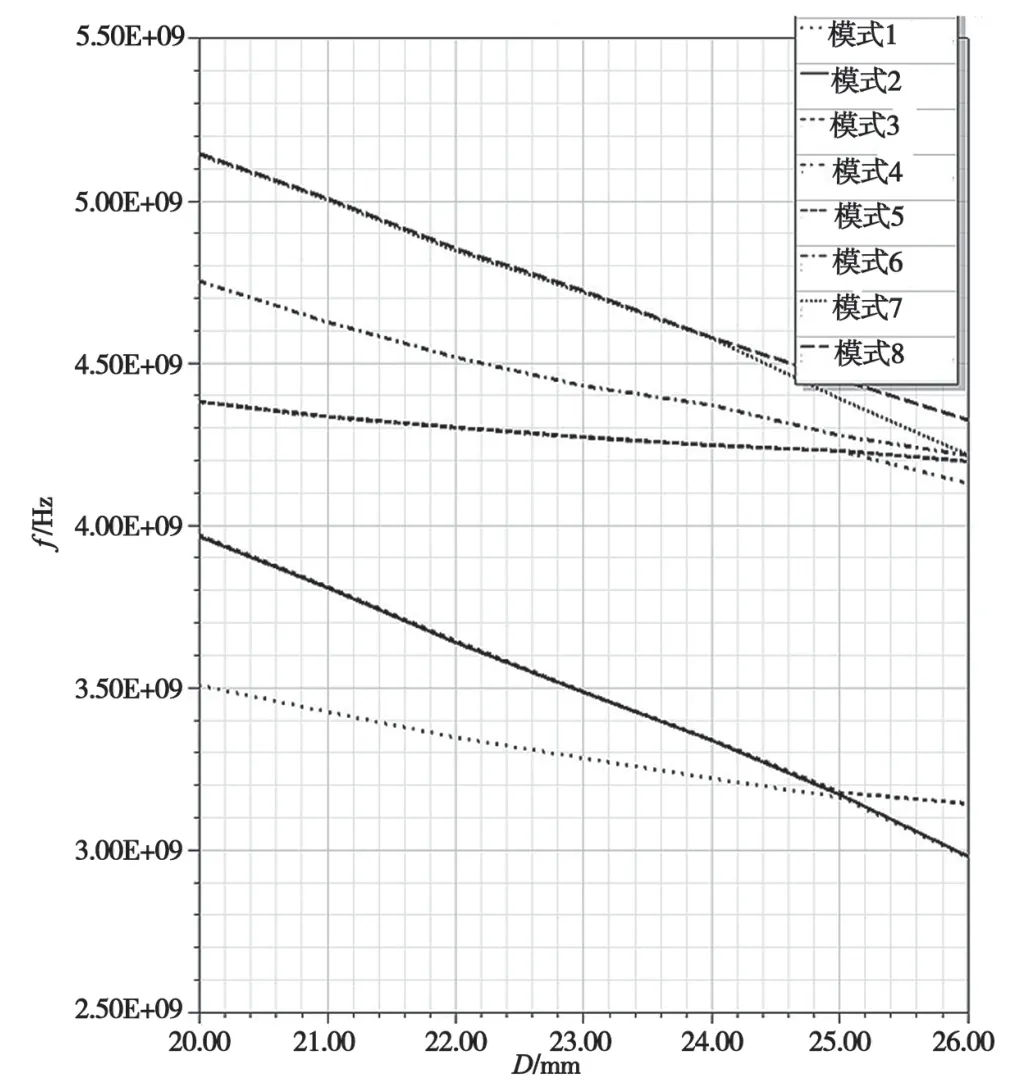
图8 介质谐振器中8 个模式的谐振频率与直径D 的关系

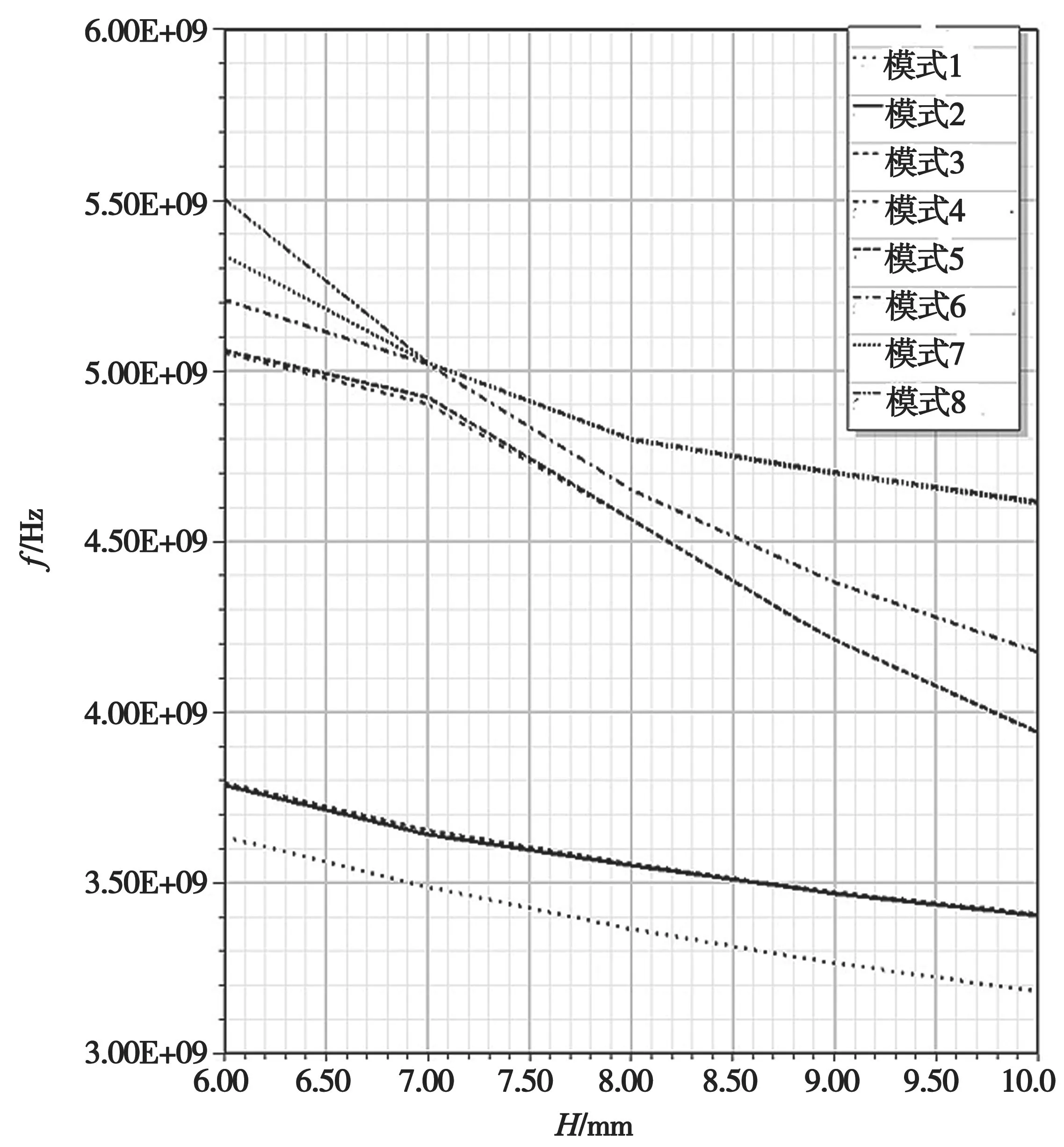
图9 介质谐振器中8 个模式的谐振频率与厚度H 的关系

根据以上的分析，从图8 和图9 的规律中挑选合适的尺寸，可初步判断当介质谐振器的直径D=23mm、厚度H=9mm 时，TE01δ模式的频谐振率接近所需的中心频率3.35GHz。当介质谐振器直径D=24mm、厚度H=9.5mm 时，HEE11 模式的频谐振率接近3.36GHz。

2 对称零点滤波器的理论设计

2.1 对称零点滤波器的理论设计

所设计的对称零点滤波器的性能指标如表1 所示，介质谐振块和金属外腔的尺寸如表2 所示。

表1 对称零点滤波器的设计指标

表2 对称零点滤波器的规格

基于以上的设计指标，采用HEE11 简并耦合双模实现两个谐振器间的耦合，输入输出分别与两个模式耦合。传输零点的产生基于信号的多径传输，并在有限频率上相位相反、相互抵消。在腔体内，信号有多条路径可以从输入端传输到输出端，因此恰当的优化设计可以实现对称零点的设计。

利用双模谐振器设计对称零点滤波器的主要难点是端口耦合的设计和模式之间的耦合设计，传输零点的设计主要通过调谐螺钉进行优化。

2.2 端口耦合的设计

端口耦合指输入端与第一个谐振器的耦合和输出端与最后一个谐振器的耦合。端口耦合采用探针耦合的方式实现，采用常见的便于制造和加工的SMA 端口，将SMA 连接器焊接在双模谐振器上作为输入输出端口。如图10 所示，两个探针伸入圆柱形谐振器的底部，实现端口耦合。

图10 内导体探针深入谐振器底部

端口耦合的强弱可以用有载Qe值来表示，即输入、输出端口的位置一般通过有载Qe值来确定。有载Qe值与耦合系数的关系为：

式中，k01为输入端口与第1 个模式之间的耦合系数。根据图5～图7 的各模式电场方向图可知，在圆柱形介质的底部深入SMA 探针，SMA 探针与相对应的谐振模式产生电耦合。耦合强弱与内导体探针伸入介质的深度成正比。但是，SMA 的内导体探针的插入深度也会影响谐振器的Q值，因此综合考虑探针深度取15.5mm。

2.3 模式间的耦合与调谐设计

耦合系数的计算可以根据式（31）进行估算：

其中，k表示两个谐振器间的耦合系数，f1表示第一个谐振器的谐振频率，f2表示第二个谐振器的谐振频率。

正如图5～图7 所展示的各模式电场图分布情况，如图11 所示，在圆柱形介质上方插入金属螺钉实现微扰可以改变HEE11 场的分布，从而实现两种模式的耦合。它的耦合系数如图12 所示。

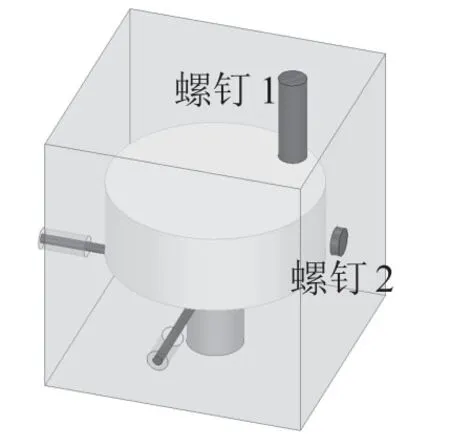
图11 微扰耦合螺钉的位置

图12 螺钉1 的长度与耦合系数的关系

3 对称零点滤波器的设计与仿真

根据端口耦合和各模式之间耦合系数的关系，使用三维电磁场仿真软件（HFSS）对滤波器进行仿真。正如分析所述，SMA 内导体长度会影响滤波器的性能，谐振器半径、高度等参数也对滤波器的性能有极大影响。针对图11 的结构，详细分析耦合螺钉对滤波器性能的影响，可以看出耦合螺钉1 的长度改变了滤波器的带宽，如图13 所示。经过多次优化分析，最终建立的对称零点滤波器结构参数如表3 所示。

图13 螺钉1 的长度对滤波器带宽的影响

表3 对称零点滤波器的初始尺寸与优化尺寸

对最终建立的滤波器结构使用三维电磁场仿真软件进行仿真，精确仿真后可得到滤波器的带宽为3.33～3.37GHz，回波损耗＞21dB，插入损耗＜0.2dB，在通带左侧的零点是3.126GHz，通带右侧的零点是3.647GHz（如图14 所示），驻波比＜1.21（如图15 所示）。

图14 滤波器的回波损耗与插入损耗

4 对称零点滤波器的仿真与实测比对

所设计的对称零点滤波器经过实物测试，并与仿真结果进行比对，结果如图16 和图17 所示。可见，实物测试与仿真结果基本一致。从S参数和驻波比的结果来看，实物测试结果比仿真频率偏差在1MHz 左右，主要原因在于加工谐振器的误差。这种假设通过HFSS 仿真得到了验证。

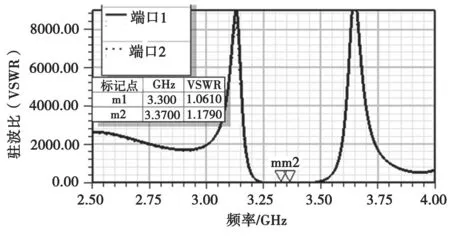
图15 滤波器的驻波比

图16 仿真与实测S 参数对比

图17 仿真与实测驻波比对比

5 结果与讨论

本文介绍了基于双模谐振器的对称零点滤波器的设计方法，利用单腔谐振器对不同的场分布有无穷多个谐振模式和谐振频率，在单个谐振器中加入一些微扰（如螺钉、开槽、切角或加入小的贴片、内切角等），采用加入调谐螺钉的方式改变原正交简并模的电场分布，使得正交简并模之间发生耦合，而两个耦合简并模的作用相当于两个耦合谐振器，从而在保持谐振回路不变的情况下，使谐振器的个数减少一半，大大减小了滤波器体积，并在通带两边各引入一个传输零点，提高了滤波器的带外抑制能力。文章利用多模谐振器的HEE11简并双模模式，设计了一种对称零点滤波器。结果显示：在通带内回波损耗＞20dB，插入损耗＜0.25dB，在通带左侧的零点为3.13GHz，通带右侧的零点为3.67GHz，驻波比＜1.21。

此外，文章分析了TE01δ，HEE11 径向顺时针45°极化模式的电场图和HEE11 径向逆时针45°极化模式的电场图。利用HEE11 径向顺时针45°极化模式和HEE11 径向逆时针45°极化模式，在两个模式电场较强的地方插入螺钉的方式影响场分布，使得模式之间发生耦合，控制螺钉的大小和插入深度，以控制耦合的强弱。输入输出的耦合通过探针的方式实现，探针插入谐振器的底部的长度控制耦合的强弱，进而实现滤波器的各项参数指标。最后，设计的滤波器经实物测试后，与仿真结果有一定偏差，频率偏差在1MHz 左右。分析发现，主要原因是谐振器制造工艺的偏差，谐振器的直径和长度都会影响谐振器的谐振频率，从而影响中心频率，同时也会影响输入输出的耦合强度。综合分析调谐螺钉长度对滤波器综合性能的影响，结果表明，调谐螺钉的长度会影响滤波器的带宽，长度越长，带宽越宽，且螺钉长度对滤波器的带宽影响是线性可控的。

本文在双模谐振器的基础上设计了一种对称零点滤波器，可以作为多模滤波器研究的参考。