基于残差网络的海洋温跃层分析方法

初 晓, 孟祥鹤哲, 张 凯, 胡成全,

(1. 长春财经学院 信息工程学院, 长春 130122； 2. 吉林大学 计算机科学与技术学院, 长春 130012)

海洋跃层[1]指海水中某些水文要素(如温度、 盐度和密度等)在垂直方向上出现突变或不连续剧变的水层, 主要用于区别上下层海水的物理性质, 也称为飞跃层, 是研究海洋生物多样性的重要因素, 在声波探测、 水下通信等领域应用广泛. 关于海洋跃层的研究目前已有很多结果[2-4]. 文献[5]提出了利用拟阶梯函数逼近法研究标准温跃层及存在逆温层的温跃层, 较好地拟合了温度曲线； 文献[1]对复杂海域存在多个厚度较薄的跃层, 提出了一种筛选温跃层和合并温跃层的方法, 并对不等距微分法、 垂直梯度法和七点二次平滑算法的优缺点进行了对比分析； 在此基础上, 文献[6]阐述了垂直梯度法和最优分割法, 并分析比较了这两种方法在确定温跃层上下边界时的性能； 文献[7]提出了一种基于熵值法获取得分, 并以此作为判断标准的新方法, 在定量分析温跃层的同时, 实现了对温跃层样本的定性分析. 本文基于上述研究成果, 对三层残差网络模型进行改进, 将改进模型用于温跃层分析判定, 并通过实验证明其对世界海洋地图集2013(WOA13)海洋区域数据温跃层分类的有效性.

1 神经网络

1.1 卷积神经网络 卷积神经网络(convolutional neural networks, CNN)是一类包含卷积计算的特殊人工前馈神经网络, 近年来被广泛应用于计算机视觉、 自然语言处理及模式识别等领域. 卷积神经网络有两个特征： 局部感知和卷积核参数共享. 局部感知是指每层的神经元只与其上一层部分神经元连接即可, 只进行局部感知, 而不是整体感知. 但如果程序中只应用局部感知理论, 会导致网络参数过大, 需对卷积核参数进行共享, 从而进一步压缩权重[8]. 图1为卷积神经网络的总体结构. 随着图形处理器(GPU)的推广, 卷积神经网络得到迅速发展, 其优异的特征提取功能在各领域被广泛应用.

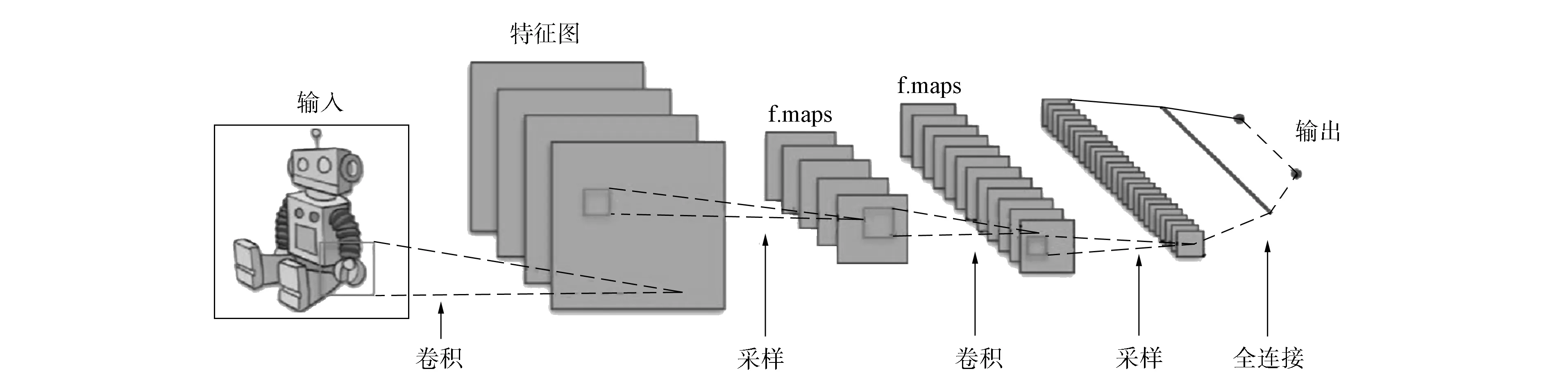
图1 卷积神经网络结构

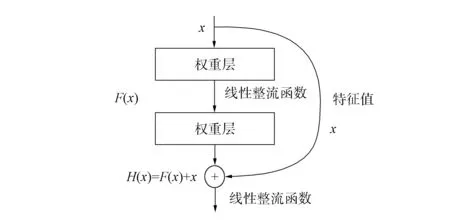
图2 残差网络基本结构

1.2 残差网络 深度学习的主要问题是梯度消失和梯度爆炸, 传统解决方案均基于数据的初始化和正则化, 虽然解决了梯度问题, 但随着网络深度的不断增加, 出现了正确率开始饱合下降及网络的退化问题. 残差单位的提出不仅解决了退化问题和梯度问题, 还兼顾了网络性能的提升. 残差网络的基本结构如图2所示.

残差单元的基本思想是解决在信息输入时因精度提高和卷积层数过多而导致的饱和, 以及随着网络深度的增加而导致准确率降低的问题. 本文假设x为信息输入,H(x)为特征输出, 则残差公式为

F(x)=H(x)-x.

(1)

残差网络是为了将学习目标由原始的完整输出H(x)变为残差公式F(x). 输入值x可与后面的层直接相连, 使后面的层可直接学习残差值, 即残差连接(skip connect)中的短连接结构(shortcut), 短连接可实现多层次的跨越, 通过执行恒等映射实现增加网络深度的目的. 残差单元计算公式为

xl+1=f[xl+F(xl,Wl)],

(2)

其中：xl和xl+1分别为第l个残差单元的输入和输出；f表示激活函数;W为卷积核;F表示残差函数. 当残差为0时, 堆积层只做恒等映射, 保证网络性能不下降, 但实际上残差不可能为0, 这也实现了堆积层在输入特征基础上学习到新的特征, 从而拥有更好的性能.

2 数据处理

2.1 数据集 WOA13是一组基于各种现场测量得出的海洋气候变量的网格化字段集, 其主要描述海洋温湿度、 磷酸、 硅酸和硝酸盐度等数据, 数据集分别包括年度周期、 季节周期和月份周期对世界海洋数据进行的统计, 是研究海洋对地球气候和环境影响的重要数据源之一[9]. 本文在对WOA13数据预处理的基础上, 对全球海洋按照测量点进行区域划分, 并对其进行基于温跃层的二分类处理, 将处理后的两类数据分别作为训练集和测试集, 然后使用Keras(人工神经网络库)+TensorFlow(基于数据流编程的符号数学系统)框架, 对实验结构进行对比, 选取针对WOA13三维海洋数据最适合的分类网络结构.

2.2 温跃层分析方法 对海洋温跃层的分析, 首先需确定水体分层的厚度. 设z表示水体分层的厚度(单位: m), 具有平衡噪声抑制和分辨率的作用. 如果z取值过大, 则将导致计算所得温度梯度变化不明显； 如果z取值过小, 则会因为采样点较少而导致梯度估计时噪声较大. 现有针对温跃层的常用探测方法中, 都是根据经验确定z值, 对温跃层的探测无法完全自主实现.

其次需要确定分层的边界值. 目前具代表性的温跃层探测有3种方法： 峰值法、 平均梯度法和最优分割法. 峰值法是根据计算得到的温度梯度峰值点求对应深度的方法, 根据峰值点分别向上、 向下进行一定距离的扩展, 以此确定温跃层的上下边界, 这种计算方法的优点是算法简单, 但扩展的距离仍依赖人为经验进行选取, 不能实现自适应性. 平均梯度法是利用垂直水层的探测值计算平均温度梯度, 并以计算结果为阈值确定温跃层的方法, 如果温度梯度高于阈值, 则视当前水层在温跃层内, 这种方法主要应用于温跃层分布相对均匀的海域. 最优分割方法是指通过对有序样品进行聚类分析的方法, 在温跃层分析时对水温剖面进行分层, 分为三层结构: 上层为均匀层, 中层为温跃层, 下层也是均匀层. 利用两次求解最优二分割的方式得到最优三分割, 以此为依据将温度梯度分为3 组, 实现分割后各组内部差异性最小, 且组与组间实现差异性最大. 最优分割法计算较复杂, 通常应用离线计算.

2.3 温跃层计算方法 温跃层是水下温度迅速下降的、 介于上层薄温水层和下层厚冷水层之间的一层海水层, 其温度和密度变化较大, 分布于不同海域的不同位置. 因为海水中盐度几乎是稳定的, 压力对密度几乎没有影响, 所以海水的水温成为最重要的影响因素, 温跃层内海水的温度和密度变化迅速, 因此成为海水分层的重要标志. 目前温跃层分析方法主要有数值函数分析法、 拟阶梯函数法、 S-T法和垂向梯度法等. 温盐剖面数据的分辨率可能存在不均匀的情形, 因此可采用不等距微分法和垂直梯度法相结合计算要素的垂直梯度, 获取温跃层特征值, 达到观测数据的合理利用, 从而获取跃层的特征值信息. 其基本原理如下.

设观测的层数为n层, 对应的层深数组为A, 要素数组为N. 在数据空间间隔均匀的情形下可直接采用垂直梯度法, 其基本原理为

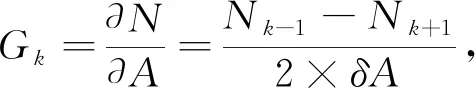
(3)

其中：G表示要素的垂直梯度；N表示某一层要素；A表示某一层水深；K表示层深序号. 在数据空间间隔不均匀的情形下可采用不等距微分法, 基本原理为

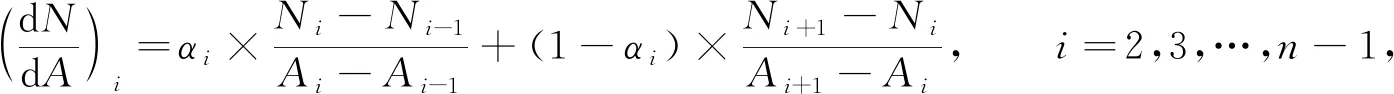
(4)

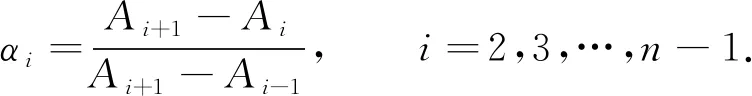
(5)

对于边界值, 即i=1和i=n处, 使用蛙跳公式(后差公式, 前差公式)法进行计算：

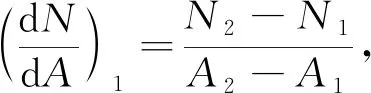
(6)

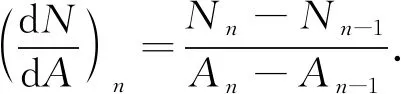
(7)

2.4 神经网络选取 确定温跃层区域后, 本文将23 940块海洋区域三维数据按2∶1分为训练集和测试集, 即训练集包含15 960块海洋区域三维数据, 测试集包含7 980块海洋区域三维数据, 所有模型均训练20次, 结果列于表1. 由表1可见, 效果最好的ResNet-18模型对海洋三维数据的分类准确率最高, 为90.425 4%, 说明残差网络模型对海洋区域三维数据的分类在性能上优于其他模型, 也证明了对于图像分类性能极强的残差网络同样适用于海洋三维数据, 所以本文将选取残差网络作为基于WOA13海洋数据温跃层分析的网络模型, 并对其进行改进.

表1 不同网络模型的实验结果对比

3 基于改进残差网络的温跃层分析

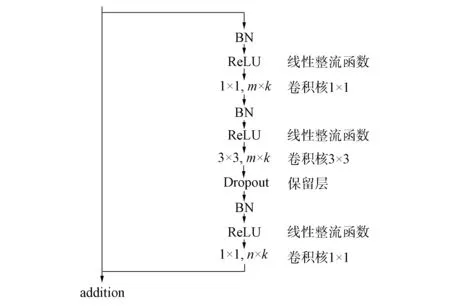
图3 改进的三层残差单元

3.1 残差网络残差单元的改进 本文基于新型的ResNet V2结构对残差单元进行改进, 将原来的二层残差单元改进为三层, 将原来大小为3×3的2个卷积层改为3个卷积层, 其卷积核大小分别为1×1,3×3,1×1. 改进的三层残差单元如图3所示， 其中：m,n为通道数量；k为加宽因子. 使用三层卷积的优势在于首层和末层中的1×1卷积可减少模型的参数, 同时可加速训练过程; 3×3的卷积层可提升性能, 减少参数, 且将AlexNet中的Dropout保留层加入到3×3的卷积层中, 能更好地减少过拟合问题.

改进后的残差单元公式为

xl+1=xl+W3σ{W2σ[W1σ(xl)]},

其中：xl表示第l层的输入；xl+1表示第(l+1)层的输出；σ表示BN和ReLU函数；W表示卷积核. 通过改进, 残差单元网络层数增加了一层, 因此本文将ResNet-18网络改进为ResNet-26网络.

在第一个卷积层中, 卷积核大小为7×7, 通道数为64, 步长为1; 最大池化层为2×2, 步长为2. 经过最大池化层后, 再经过2,3,4,5四个卷积组， 每个卷积组中残差单元数为2, 卷积组2的残差块结构为： 1×1, 通道数64； 3×3, 通道数64； 1×1, 通道数256. 卷积组3的残差块结构为： 1×1, 通道数128； 3×3, 通道数128； 1×1, 通道数512. 卷积组4的残差块结构为： 1×1, 通道数256； 3×3, 通道数256； 1×1, 通道数1 024. 卷积组5的残差块结构为： 1×1, 通道数512； 3×3, 通道数512； 1×1, 通道数2 048. 平均池化层是最后一层, 尺寸为4×4, 输出1×1×4 096, 该层需经历一个全连接层Softmax函数, Softmax函数包含5个神经元. 为进一步证明改进的残差单元对WOA13海洋数据分类的准确性优于原模型, 本文设计4组对比实验, Dropout设为默认值0.5, 其结果列于表2.

表2 残差单元改进对比实验结果

3.2 超参数选取 超参数的设置直接影响网络性能. 本文分别针对首层卷积核的大小、 Batch Size(批大小)、 残差单元数量及加宽因子进行实验, 通过不断控制变量, 选取不同超参数进行实验. 实验结果表明, 本文最终的超参数选择为： 第一层卷积核为7×7, Batch Size为64, 残差块个数为2, 加宽因子为1. 经过超参数调整, ResNet-26对海洋三维数据的分类最高准确率提高了0.5%.

图4 改进的ResNet-26实验数据结果

3.3 保留率设置 上述实验虽已验证了在AlexNet网络模型基础上加入保留层(Dropout)的三层残差单元ResNet-26网络模型对海洋三维数据进行二分类有效, 但Dropout的设置对准确率有一定影响. 本文分别对保留率为0.4,0.5,0.6,0.7,0.8这5种情形进行实验. 实验结果表明, 在其余参数均与上述实验相同的情形下, 保留率为0.7时, 准确率达到峰值95.103 8%. 应用改进后的ResNet-26对数据进行二分类实验, 实验结果如图4所示, 其中: 蓝色实线表示训练结果; 黄色虚线表示测试结果.

为保证实验结果的准确性, 本文利用WOA13数据集中全球海域的月级别平均数据, 对1995—2012年的2月、 5月、 8月和11月平均海洋数据进行实验, 不同月份数据实验对比结果列于表3. 由表3可见, 本文方法可行、 有效.

表3 不同月份数据的实验结果对比