新能源站侧规模化应用储能的电力系统运行模拟

冉 亮，郭建华，袁铁江

(1.国网甘肃省电力公司，甘肃 兰州 730000；2.大连理工大学电气工程学院，辽宁 大连 116024)

0 引言

随着电力系统中可再生能源并网容量的不断提升，其出力的随机性和间歇性对电网规划、运行等方面的影响日益突出。通常在系统中加入储能设备，以确保接入后电网的安全稳定[1-2]。

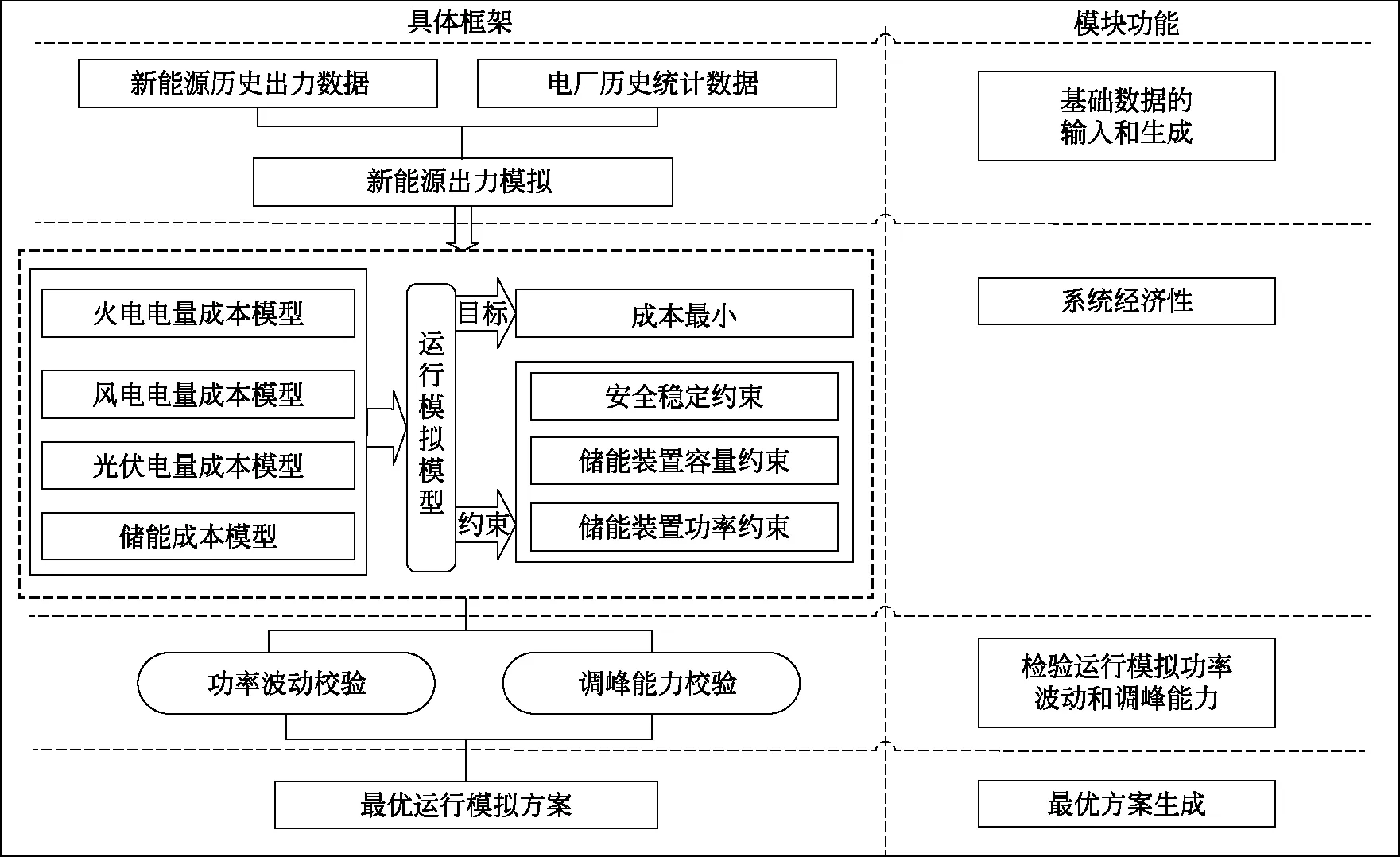
图1 含储能的新能源系统运行模拟框架

文献[3-4]利用储能跟踪风光联合系统的出力变化，以消除其不确定性带来的功率波动影响；文献[5]提出了"电力系统柔性生产模拟"的概念，考虑不确定性电源和储能接入下的容量可信度以及可避免费用等；文献[6]就风光储联合系统中储能的“削峰”作用进行研究；文献[7]利用风速和负荷预测误差的概率分布函数来描述系统中存在的不确定性因素，建立了基于风险备用约束的含风电场电力系统动态经济调度新模型；文献[8]计及风电在环境方面的贡献，建立了含大型风电场和储能装置的清洁经济调度数学优化模型。

上述文献的研究重点大多在讨论生产模拟的经济性，对于接入储能对电力系统的具体影响未做分析。为此，本文提出含储能的新能源电力系统运行模拟框架。该框架中的核心方法和技术包含：新能源出力模拟技术、以成本最小为目标运行模拟以及电力系统的平抑功率波动和调峰能力校验。框架的创新之处在于利用新能源波动和调峰能力的指标对运行模拟结果进行校验，量化储能对电力系统的影响，更为全面地评估了新能源站侧规模化接入储能的作用。

1 电力系统运行模拟框架

本文建立的含储能的新能源电力系统运行模拟框架主要包括基础数据的输入和生成、系统经济性、新能源功率波动和调峰能力检验以及最优方案生成四个部分。

合理有效的新能源出力模拟是电力系统运行模拟保证模型可靠性的首要环节[9]，本文采用反向传播神经网络 (back propagation，BP)方法有很好的非线性拟合性与自适应性[10]。

含储能新能源系统的短期随机生产模拟技术是实现电力系统运行模拟经济目标的关键环节。首先构建运行模拟模型，主要包括火电、风电、光伏电量成本模型以及储能成本模型。运行模拟模型以经济成本最小为目标函数，以电力平衡约束、火电机组爬坡约束、电量平衡约束、储能装置充放电约束以及储能装置容量约束等作为约束条件。

对运行模拟结果进行新能源功率波动和调峰能力校验是判断运行模拟方法可行性的必要环节。通过校验之后，得到最优调度结果。含储能的新能源系统运行模拟框架如图1所示。

2 新能源功率波动和调峰能力评估指标

本文将接入储能前后系统的新能源功率波动和调峰能力作为判断指标，通过比对其指标的提升效果，更好衡量新能源站侧规模化接入储能对风光出力的调节作用。

选取新能源功率变化率作为储能平抑功率波动的评估指标，新能源平均功率变化率表示在评估周期内，新能源所提供的功率在时段的平均变化率，新能源功率变化率的计算式为

式中：P(t)为时段t内新能源功率；PW、PPV分别为风电、光伏出力；PSi、PSo分别为储能系统充电功率、放电功率。

为了更直观说明电网系统调峰能力，本文引入了反调峰概率(PFTF)指标，以此量化储能接入对系统调峰能力的影响程度，反调峰概率计算思路为：在一定周期内，发生反调峰时段与总采样时段的比值，具体计算过程参考文献[11]。

3 系统运行模拟模型

3.1 目标函数

系统发电成本包括火电电量成本、风电电量成本、光伏电量成本以及储能成本，各项成本如下。

3.1.1 火电电量成本模型

影响火电电量成本的因素有火电名义环境补偿成本和火电营运成本。火电名义环境补偿成本FNEPT(t)为

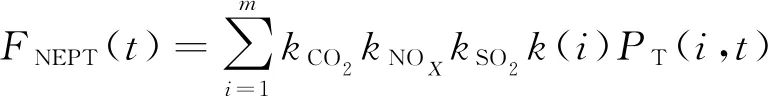
(3)

火电营运成本FTOP(t)为

(4)

在某时段t内火电电量成本VT(t)为

VT(t)=FNEPT(t)+FTOP(t)

(5)

式中：m为系统的火电机组数目；kCO2、kNOx、kSO2分别为CO2、NOx和SO2排放系数，ki为供电煤耗系数；PT(i,t)为在t时段内第i台火电机组的出力；pTOP(i,t)为在t时段内第i台火电机组不计入火电机组的名义环境补偿成本的火电价格。

3.1.2 风电电量成本模型

风电电量成本包括风电场营运成本、基于极限穿透功率的风电场负效率运行惩罚成本和基于风电场出力预测可信度的风电旋转备用容量补偿成本[12]。风电场营运成本FWOP(t)为

(6)

基于极限穿透功率的风电场负效率运行惩罚成本FNEPWF(t)为

(7)

式中：pWOP(j,t)为时段t内第j个风电场出力的营运价格；PW(j,t)为时段t内第j个风电场的出力；pN(t)为在时段t内的风电场负效率功率(negative efficiency power of wind farm，NEPWF)价格；PWF(j,t)为时段t内第j个风电场的预测出力；PWLPP(j,t)为时段t内第j个风电场的极限穿透功率。

基于风电场出力预测可信度的风电旋转备用容量补偿成本FWRC(t)为

(8)

式中：pC(t)为系统在时段t内的备用容量价格；EW(j,t)为时段t内第j个风电场预测出力的可信度；n为系统中的风电场数量。

某时段t内风电电量成本VW(t)为

VW(t)=FWOP(t)+FWRC(t)+FNEPWF(t)

(9)

3.1.3 光伏电量成本模型

光伏电场内外部成本包括光伏电场运营成本和基于光伏出力预测可信度的光伏旋转备用容量补偿成本。光伏电场运营成本FPVOP(t)为

(10)

基于光伏出力预测可信度的光伏旋转备用容量补偿成本FPV(t)为

(11)

时段t内光伏电量成本VPV(t)为

VPV(t)=FPVOP(t)+FPV(t)

(12)

式中：PPV(k,t)为第k个光伏场在时段t内的出力；fpcos(t)为光伏在时间段t的发电成本电价，其值由发电厂商决定；EPV(k,t)为第k个光伏电场预测出力在时段t内的可信度；PPVF(k,t)为第k个光伏场在时段t内的预测出力；x为系统中的光伏电场数目。

3.1.4 储能日成本数学模型

综合考虑储能初始投资成本、运行维护成本，建立储能系统日成本模型。初始投资成本F1为

F1=FPPc+FEAc

(13)

储能系统的年运行维护成本F2为

F2=FmPc

(14)

根据储能系统的使用寿命年限和贴现率，将储能系统全寿命周期内的成本进行分摊，并与储能系统的年运行维护成本叠加，得到储能系统的日成本VS为

(15)

式中：FP为储能系统单位功率成本；Pc为储能电池额定功率；FE为储能系统单位容量成本；Ac为储能电池额定容量；Fm为单位容量的年运行维护成本；r为储能系统贴现率；T为储能装置使用年限。

3.1.5 运行模拟成本模型

根据上文建立的火电电量成本模型、风电电量成本模型、光伏电量成本模型以及储能成本模型，得到运行模拟模型的目标函数为

minFT=VT(t)+VW(t)+VPV(t)+VS

(16)

式中FT为总发电成本。

3.2 约束条件

(1) 系统功率平衡约束

(17)

式中PD(t)为系统时段t内的负荷。

(2) 机组的出力约束。

火电机组出力约束

PTmin(i)≤PT(i,t)≤PTmax(i)

(18)

风电机组出力约束

0≤PW(j,t)≤PWF(j,t)

(19)

光伏机组出力约束

0≤PPV(k,t)≤PPVF(k,t)

(20)

(3) 火电机组爬坡约束

ζTdown(i,t)≤PT(i,t)-PT(i,t-1)≤ζTup(i,t)

(21)

式中：ξTdown(i,t)和ξTup(i,t)分别为第i台火电机组在某时段t内出力的下降率和上升率。

(4) 储能装置充放电约束

式中：PSi-max、PSi-min分别为储能装置最大充电功率和最小充电功率；PSo-max、PSo-min分别为该储能装置最大放电功率和最小放电功率；PSi(t)、PSo(t)分别为储能电装置时间段t的充电功率、放电功率。

(5) 储能电站容量约束

AS-min≤AS(t)≤AS-max

(24)

式中：AS-min、AS-max分别为储能电站最大存储容量和最小存储容量；AS(t)为储能装置在t时刻的存储容量。

4 算例分析

4.1 新能源站侧规模化接入储能的运行模拟

本文以新疆电网为例，利用神经网络方法进行新能源出力模拟，得到的典型日风电、光伏出力数据作为运行模拟仿真样本数据进行分析，该数据采用15 min为1个时间段，以24 h作为1个研究周期，总时段数为96。系统在研究周期内各时段的新能源预测出力以及电网负荷如图2—3所示。

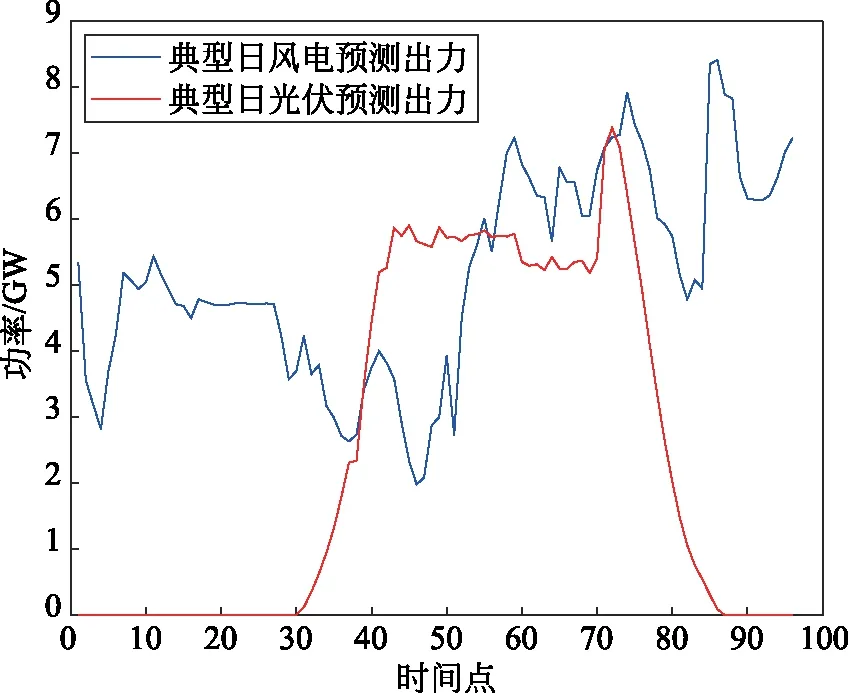
图2 典型日新能源预测功率

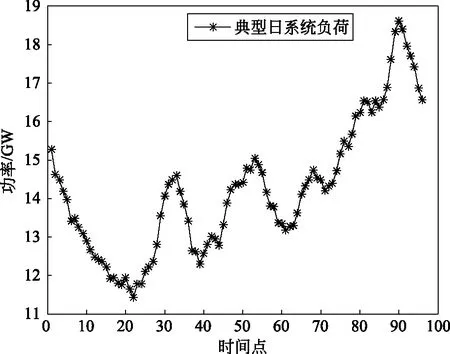
图3 典型日系统负荷

其中，风电装机容量为19.251 GW，光伏装机容量为10.216 GW,火电机组装机容量约为53.770 GW;火电机组时段FE内不计入火电机组名义环境补偿成本的火电价格pTOP(t)为0.027万元/MW；kCO2为1.2万元/MW、kNOx为0.018万元/MW、kSO2为0.012万元/MW，ki为0.036万元/MW；系统的正、负备用率取为20%。风电场的极限穿透功率为12.17%；风电场在研究周期内各个时段预测出力可信度为0.85。在研究周期内的各个时段内风电场的营运价格pWOP(j,t)为0.056万元/MW。光伏电场在研究周期内各个时段预测出力可信度为0.4667；在研究周期内的各个时段内光伏电场的营运价格为0.065万元/MW。系统在各时段t内备用容量价格pC(t)为0.011 2万元/MW[13],在各时段t内的风电场负效率功率的价格pN(t)为0.03万元/MW,在各时段t内火电名义环境补偿成本的价格pNEPT(t)为0.004万元/t[13]。

本文基于遗传算法 (genetic algorithm，GA)求解新能源站侧规化应用储能的电力系统运行模拟。

图4是未接入储能时系统的出力曲线，在调度周期内最优运行成本为11 005.578万元。可以看出，新能源大规模并网在实际运行过程中如果没有储能设备加以控制，新能源电站本身的有功输出波动较大，给电网调峰运行带来了极大压力。

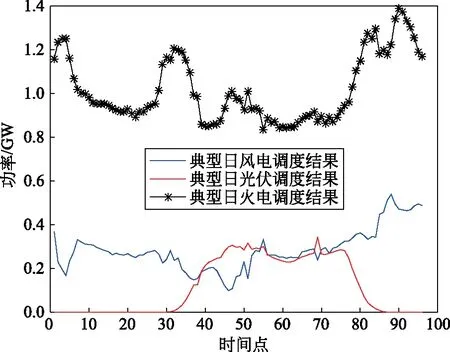
图4 典型日未接入储能调度结果

储能电站功率为2.250 GW，储能容量为12 GW·h；参数参考文献[14-15]储能系统单位容量成本FE为350万元/(MW·h)，储能系统单位功率成本FP为435万元/(MW·h)，储能单位容量的年运行维护成本Fm为30万元/(MW·h)，储能系统贴现率r为8%，储能装置使用年限T为15年。

图5为接入储能之后的典型日火电、新能源调度结果，图6为储能的充放电功率，在调度周期内最优运行成本13 014.199万元。结合图2—3可以看出：在1—30时间段内，系统低负荷运行，储能电站多数时刻处于充电状态；在30—40时间段内，系统低负荷运行，但风场出力较为充足，所以此时火电出力逐步降低，储能电站处于充电状态；38—50时间段内，系统负荷处于较低水平，新能源电场出力增多，弃风弃光减少，同时储能开始充电，火电机组出力逐步降低；86—96时间段内，系统负荷逐步降低，新能源电场出力开始下降，储能电站开始放电。对比图4—5，储能系统接入后，在典型日调度周期内，新能源电场增发了2.17×107kW·h,新能源站侧应用储能提高了新能源利用率。

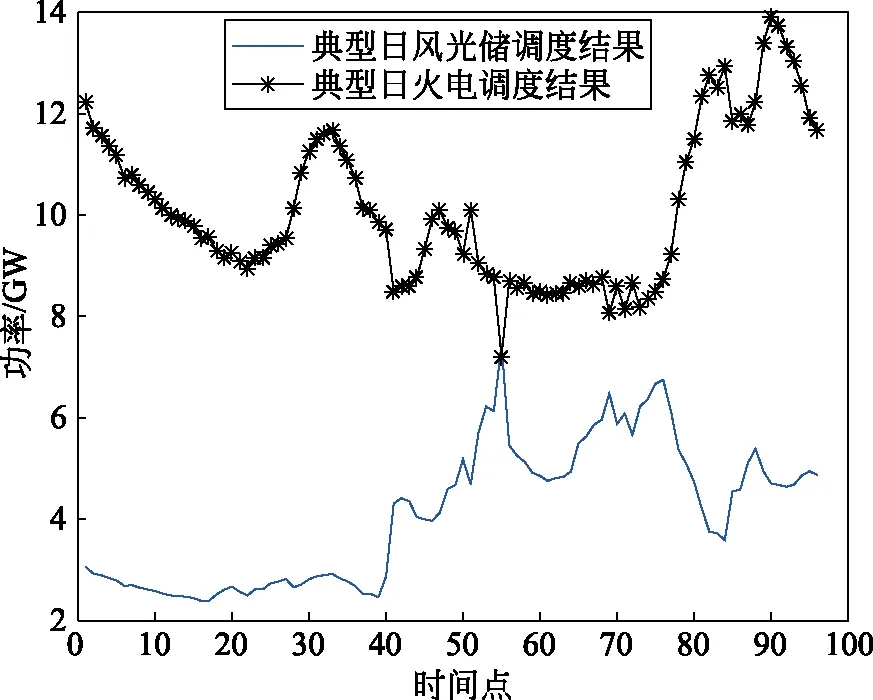
图5 典型日风光火储调度结果

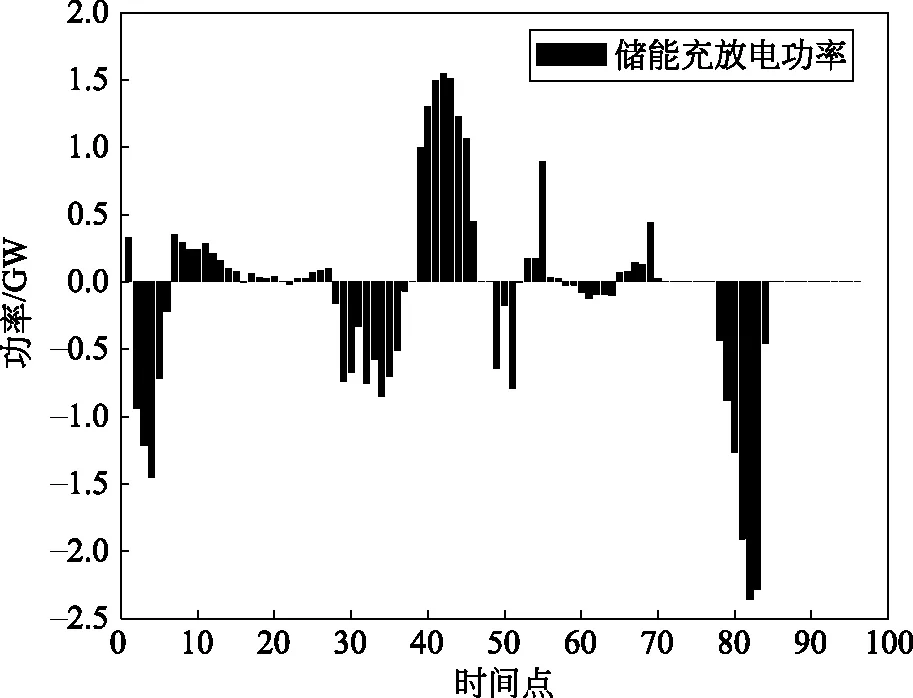
图6 典型日储能充放电功率

对接入储能前后进行新能源功率波动及调峰能力评估，量化新能源站侧规模化应用储能对系统的影响，其结果如表1所示由表1可知，在接入储能电站后，系统波动率指标明显下降，变化率为每15 min下降7.29%，根据GB/T 19964—2012的规定，新能源电站有功功率每分钟变化应不超过10%装机容量，远远满足国家标准，说明新能源站侧规模化应用储能能够较好地平滑新能源电场的功率波动；同时，反调峰概率在接入储能后明显下降，说明规模化应用储能对反调峰现象起到了很好的抑制作用。

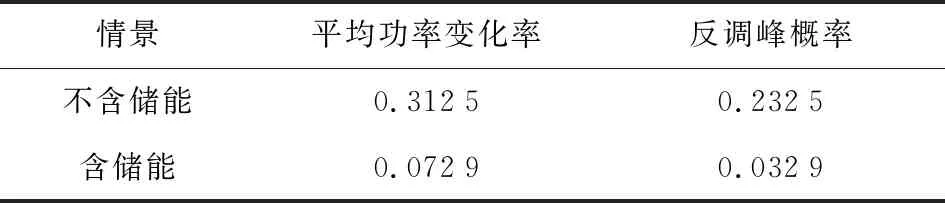
表1 系统平抑波动/调峰能力校验结果

4.2 新能源渗透率对平抑波动和抑制反调峰的影响

改变新能源渗透率，计算不同新能源渗透率下的新能源平均功率波动率和反调峰概率，图7给出了储能在不同新能源渗透率下的实时充放电功率图。

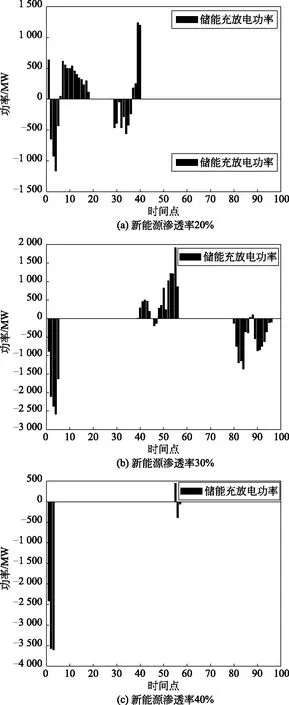
图7 新能源渗透率20%、30%、40%时储能充放电功率

由图7，由于新能源的随机性和波动性的特点，在不同时间段内，新能源的出力差别很大，所以若在整个周期使用相同的新能源渗透率会导致储能装置的利用率极低，绝大部分时段储能装置无法进行正常充放电，所以本文将1天分为2个时段，将前一时段的新能源渗透率设置为0.22，后一时段设置为0.37，这样会使极大地提高储能装置的利用率。

4.3 储能容量对平抑波动和抑制反调峰的影响

改变储能设备容量，计算不同储能容量下的新能源平均功率波动率和反调峰概率，图8给出了新能源平均功率波动率指标和反调峰概率指标随储能设备容量改变而变化的情况。

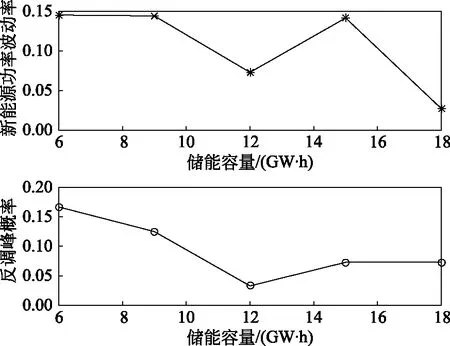
图8 功率波动率指标和反调峰概率指标随储能容量的变化情况

由图8可知，随着储能设备容量的增加，新能源平均功率波动率指标在容量为12 GW·h时处于较小值，在15 GW·h达到峰值以后，波动率会逐步下降；随着储能设备容量的增加，反调峰概率指标整体上是越来越小的，在12 GW·h时处于最低值，在12 GW·h之后，反调峰概率会开始上升，综合考虑到2种指标以及投资经济性，容量和充放电功率越大，初始投资成本越高，所以选取的储能容量为12 GW·h。

4.4 储能充放电功率限制对平抑波动和抑制反调峰的影响

改变储能设备最大充放电功率，计算不同充放电功率下的新能源平均功率波动率和反调峰概率，图9给出了新能源平均功率波动率指标和反调峰概率指标随储能设备最大充放电功率改变而变化的情况。

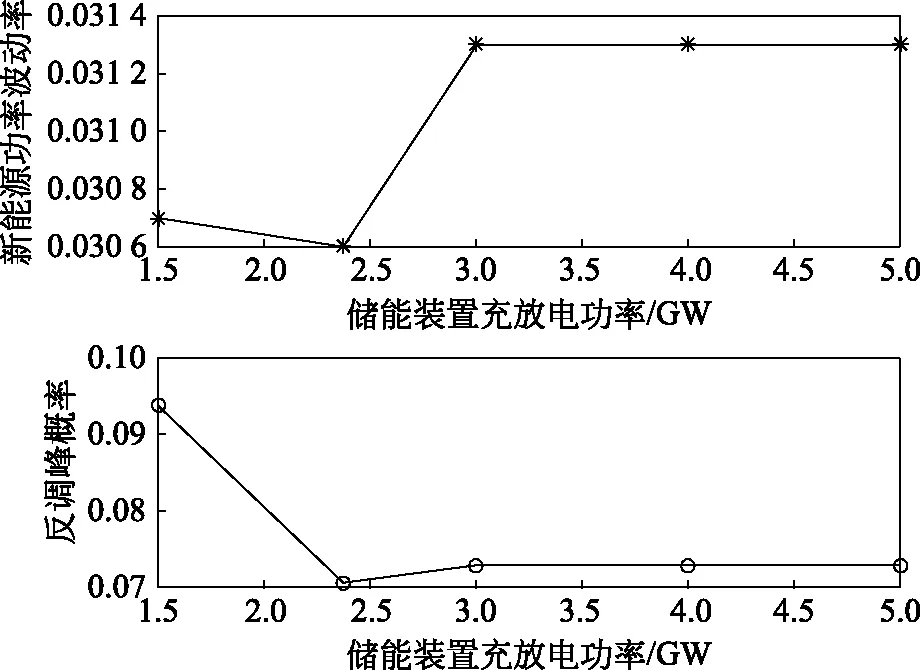
图9 功率波动率指标和反调峰概率指标随储能充放电功率限制的变化情况

由图9可知，新能源平均功率波动率会随着功率限制的增大而增大，当功率限制大于3 GW时，波动率会趋于平缓，反之，反调峰概率则会随着功率限制的增大而减小，当功率限制大于3 GW时，反调峰概率会趋于平缓，相比于新能源占比和储能装置容量对波动率和反调峰概率的影响，调整储能充放电功率对指标的改善影响较小，事实上，由于设备参数与经济投入之间的关系。

充放电限制的数值越高，设备在制造工艺上实现的难度越大，初始投资成本也越昂贵，因此在选择相应的储能设备充放电功率限制时，应根据新能源电场容量、新能源渗透率、系统规模以及储能装置容量等实际情况进行择优选择。

5 结论

(1) 本文提出了含储能的新能源电力系统运行模拟框架，以新疆电网为例进行算例分析，通过对比接入储能前后的运行模拟结果，发现接入储能对平抑波动、抑制反调峰、电网增发电量都有明显提升。又以修改新能源渗透率、储能容量、储能充放电功率限制为例进行算例分析，分析结果表明，在新能源渗透率为40%，储能容量为12 GW，储能充放电功率为2.25 GW时，接入储能对功率波动率和反调峰概率的降低贡献最明显，所以新能源站侧规模化接入储能对电力系统稳定运行有实际意义。

(2) 本文提出的运行模拟方案在经济调度和技术性评估中都是以分钟为单位进行的，通过算例也验证了方案的合理性，但考虑到电力系统实际运行中多周期协调的特点，多时间尺度协调的方案对实现电力系统精细化运行模拟可能效果更佳。