基于形态滤波的音频大地电磁去噪研究
2020-07-17陈知富
陈知富
江西省地质工程(集团)公司地球物理勘查院 江西南昌 330000
1 形态滤波原理
形态滤波法是以数学形态学为基础,通过设计一个结构元素在信号中不停地移动,对信号进行匹配并最终达到提取信号,保持信号的细节成分与抑制噪声的目的[1]。通过对一维信号处理的研究发现,形态滤波对信号的的低谷噪声、峰值噪声和白噪声都具有良好的抑制效果[2]。形态滤波算法由腐蚀与膨胀运算两种算法组成[3],一维离散信号的形态滤波过程为:
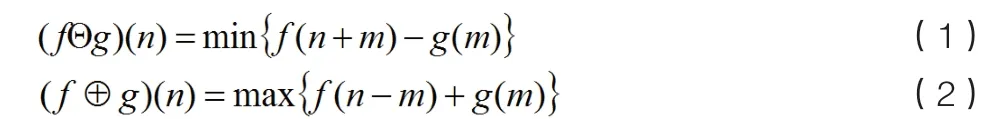
由腐蚀和膨胀运算可进一步构造开运算和闭运算,形态开(o)运算为先腐蚀后膨胀,形态闭(·)为先膨胀后腐蚀,f 关于g 的开运算和闭运算分别为:
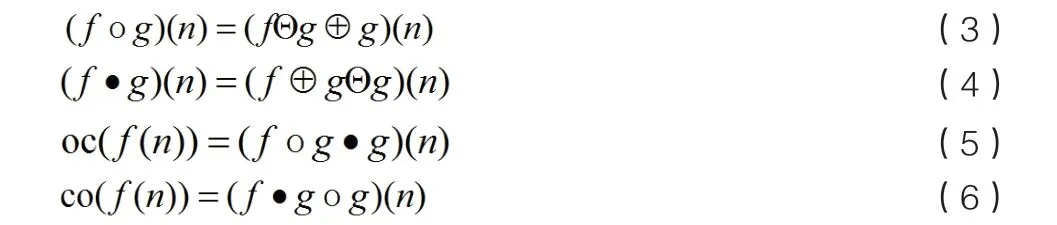
为了减少输出幅值的畸变,通常使用由开-闭和闭-开滤波器组成的组合形态滤波器对信号进行滤波:
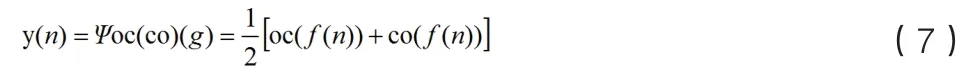
用单一的结构元素进行的形态滤波与结构元素的类型与尺度有关。比较常用的结构元素有三角形、圆盘形、直线形,抛物线型等,其中尺度指的是结构元素的高度与长度。不同类型的噪音使用不同类型的结构元素进行抑制出现到不同效果。一般来说当结构元素的大小形状和噪声的相似度比较高时具有较好的去噪效果。当信号中存在不同大小和类型的噪声时,选择单一的结构元素进行滤波的效果是有限,所以人们提出了广义形态滤波。广义形态滤波就是在形态滤波的基础上进行开-闭与闭-开计算时,要采用两种不同的结构元素,其公式如下:
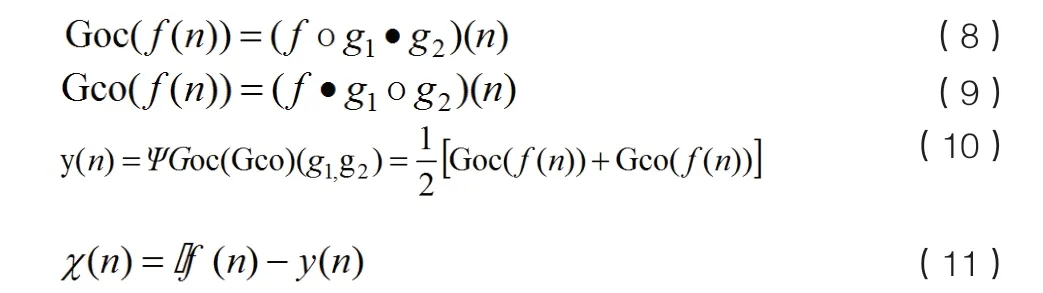
2 仿真信号分模拟析
首先生成一段仿真信号,然后加入一些野外采集过程中的常遇到的干扰噪声,例如脉冲,三角波,方波等信号,再通过选取不同结构元素进行去噪研究,分别通过选取不同形状相同尺度和不同尺度相同形状的结构元素进行滤波,从而选取最佳结构元素的滤波器进行去噪研究。
2.1 相同尺寸不同形状的结构元素的滤波效果研究
分别选取抛物线形,三角形,圆盘形,直线形的5 点结构元的结构元素滤波器对上述的加噪的信号进行滤波,对比最后的滤波效果图以及去噪前后的信号各参数,得到一种相对较好的结构元素。图1 从上至下依次为抛物线形,三角形,圆盘形,直线形的5 点结构元的结构元素滤波器的去噪效果图,左边为加噪信号,中间为形态滤波效果图,右边为去噪后信号。通过对比研究,分别经过抛物线形,三角形,圆盘形,直线形这四种形状的结构元素的形态滤波后,基本上都能去除大尺度干扰噪声,能比较好地保护原始模拟信号的特征,由此表明形态滤波能够去除一些大尺度干扰噪声。对比去噪前后的各项参数,圆盘形状结构元素的形态滤波器的去噪效果相对来说比较明显,其处理后的信号更加接近原始仿真信号的局部特征。
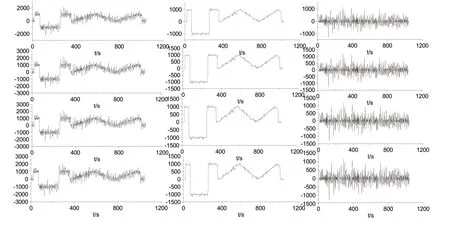
图1 不同类型结构元素滤波效果图
2.2 相同形状不同尺寸的结构元素的滤波效果研究
同样模拟同一段仿真信号,加入在EH4 系统数据采集过程中常见的而且干扰比较严重的三角波噪声。三角波噪声信号的能量比正常信号的能量大很多,所以大部分有效信号几乎湮没在噪声信号中。选取圆盘型的结构元素滤波器,分别选取3 点,5 点,9 点,13 点结构元对含噪声的仿真信号进行去噪研究,图2 从上之下依次为3 点,5 点,9 点,13 点结构元的圆盘型形态滤波效果图,左边为加噪信号,中间为形态滤波效果图,右边为去噪后信号表2 为含三角波噪声干扰的仿真信号去噪前后的各主要参数对比表。通过对比图和表格可知,随着滤波器结构元素尺寸的增加,其通过形态滤波提取出的含三角波噪声的轮廓越来越光滑,所以5 点圆盘型结构元素滤波器的滤波效果较3 点的效果更好,但是9 点与13 点圆盘型结构元素滤波器又会损害一些有效的信号,尺寸越大损害的有效信号越多。所以通过本次研究表明,5 点圆盘型结构元素滤波器对于一些野外常见的大尺度干扰噪声的去噪效果比较理想。所以在进行形态滤波的过程中应该选取不同类型和尺度的结构元素滤波器进行分析研究,选取最合适结构元素,以能使不同类型和尺度的噪声得到最好的抑制为最终目的。

图2 不同尺寸的圆盘型结构元素滤波效果图

表1 含三角波噪声干扰的仿真信号去噪前后各主要参数对比
3 实测数据去噪
在实测的大地电磁数据中,往往包含着大量的噪声干扰,例如谐波干扰,三角波干扰,方波干扰等等,而且比较难判断具体受到的哪种干扰。本小节选择对某一段包含了大尺度强噪声干扰的实测EH4 系统时间序列进行滤波,而且选择使用由圆盘型结构元素构成的组合形态滤波器,其结构元素长度为5 点。从图3(b)中可以看到,形态滤波把时间序列曲线3(a)中“毛刺”给去掉了,最后得到了比较平滑的曲线,而且该信号曲线正是实测时间序列中混杂的大尺度强干扰噪声。最后将信号进行重构后,重构后的时间序列如图3(c)所示,基本上还原了时间序列信号的原来特征,最终得到了大地电磁的有效信号,提高了大地电磁测深资料的质量和勘探分辨率。
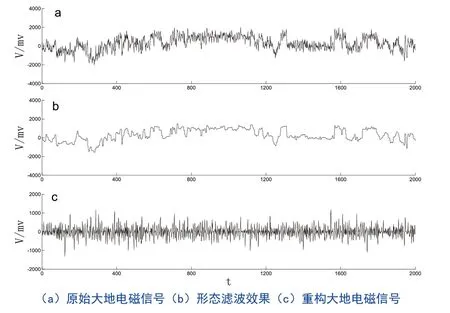
图3 实测数据去噪及重构大地电磁信号
4 结语
本文主要研究了几种大地电磁场中的常见噪声以及会产生的影响,并通过引入形态滤波对电磁信号中的噪声进行处理,详细介绍了形态滤波的基本原理,分别对加大尺度干扰噪声的仿真信号进行滤波,通过研究相同形状不同尺寸以及相同尺寸不同形状的结构元素滤波器的去噪效果,来选择最佳的结构元素,研究结果表明5 点圆盘型结构元素的滤波器的去噪效果较好,并通过处理实测数据来说明其去噪效果,结果表明形态滤波对于非平稳的信号具有一定的去噪效果。
