有/无尾喷流效应影响的导弹侧向喷流干扰数值研究

白涛涛　曹军伟　王虎干　孙振华

摘 要：为研究尾喷流效应对导弹尾端直接力装置侧向喷流与主流流动干扰的影响，采用三维流场CFD仿真方法。首先，对带X形尾舵的旋转体和带发动机的旋转体进行模拟，分别证明了所采用的计算方法对侧向喷流干扰流场和发动机尾喷流求解的能力;其次，开展了侧向喷流与主流在有/无尾喷流影响下的干扰流动数值计算，研究了0°攻角情况下尾喷流给压强分布、压力系数、对称面马赫数及流线、侧向力及力矩放大因子和后弹体流场结构带来的变化。结果表明： 尾喷流会大幅提高侧向喷流的效率;尾喷流不会改变侧向喷口上游的流场结构，但对弹体底部、尾舵后缘及侧向喷口下游区域的流场结构影响较大。

关键词： 导弹;尾喷流;侧向喷流;干扰;数值研究;直接力装置

中图分类号：TJ760;V211.3 文献标识码：A文章编号： 1673-5048（2020）03-0083-05

0 引言

当前各导弹研发机构均采用布置在弹体前部或质心位置的直接力装置来提高导弹末端机动性，但是这种直接力方案需要占据独立舱段，会增大弹体尺寸和体积，不能同时满足上述的两个要求，若将直接力装置布置在弹体尾端，并集成在舵机舱内部，就可在不影响弹体尺寸和体积的前提下提升导弹末端机动性。当然，这种直接力方案也存在一定的技术问题： 侧向喷流临近发动机尾喷流，容易与高速外流和发动机尾喷流产生复杂干扰，可能会影响导弹的气动性能。

近年来针对直接力侧向喷流的研究主要集中在攻角对侧向喷流干扰流场的影响[1-3]、喷口数量和布局对侧向喷流干扰流场的影响[4-6]、侧向喷口型面和形状对侧向喷流干扰流场的影响[7-8]、侧向喷流与舵面的相互干扰[9-10]、侧向喷流性质对侧向喷流干扰流场的影响[11-12]和侧向喷口打开及关闭过程的动态特性研究[13-14]等方面。另外，国内外大量研究也表明，发动机尾喷流会对导弹后弹体附近的流场产生显著的影响[15-19]。上述研究或是针对布置在弹体前部或质心位置的直接力裝置，或是仅研究发动机尾喷流的影响，而针对发动机尾喷流影响下的尾端直接力侧向喷流干扰流场研究鲜见报道，从装备发展和技术进步两方面来说，开展针对性的研究十分必要。

本文针对采用尾端直接力装置的带尾舵尖拱头部-圆柱弹身导弹，通过求解三维Navier-Stokes方程，开展导弹尾端侧向喷流与主流在有/无尾喷流影响下的干扰流动数值计算，研究了0°攻角情况下有/无尾喷流效应对弹体压强、压力系数、对称面马赫数及流线、侧向力及力矩放大因子和后弹体流场结构的影响，为采用尾端侧向喷流控制的导弹设计提供参考。

1 数值计算方法

1.1 物理模型及计算网格

1.1.1 物理模型

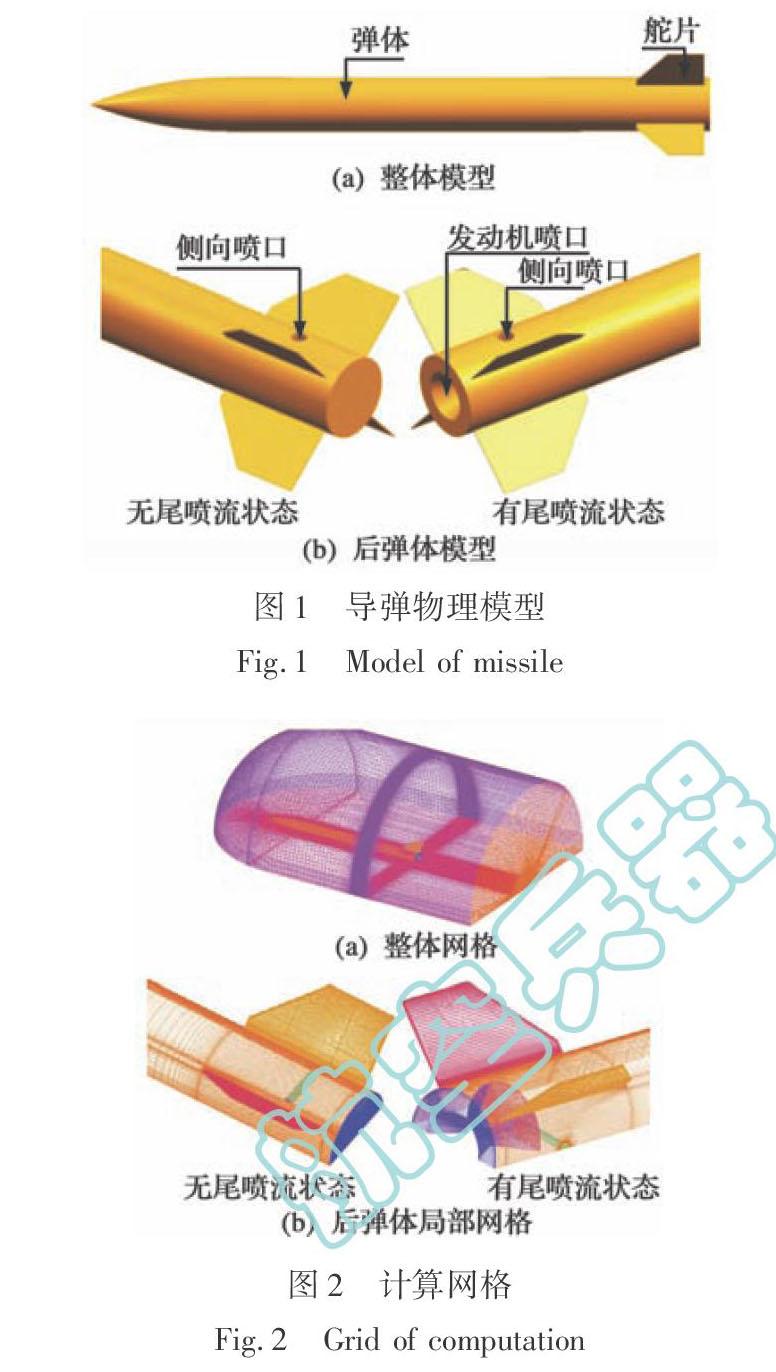
本文物理模型由弹体、舵片、侧向喷口和发动机（有尾喷流状态）组成， 具体模型如图1所示。

1.1.2 计算网格

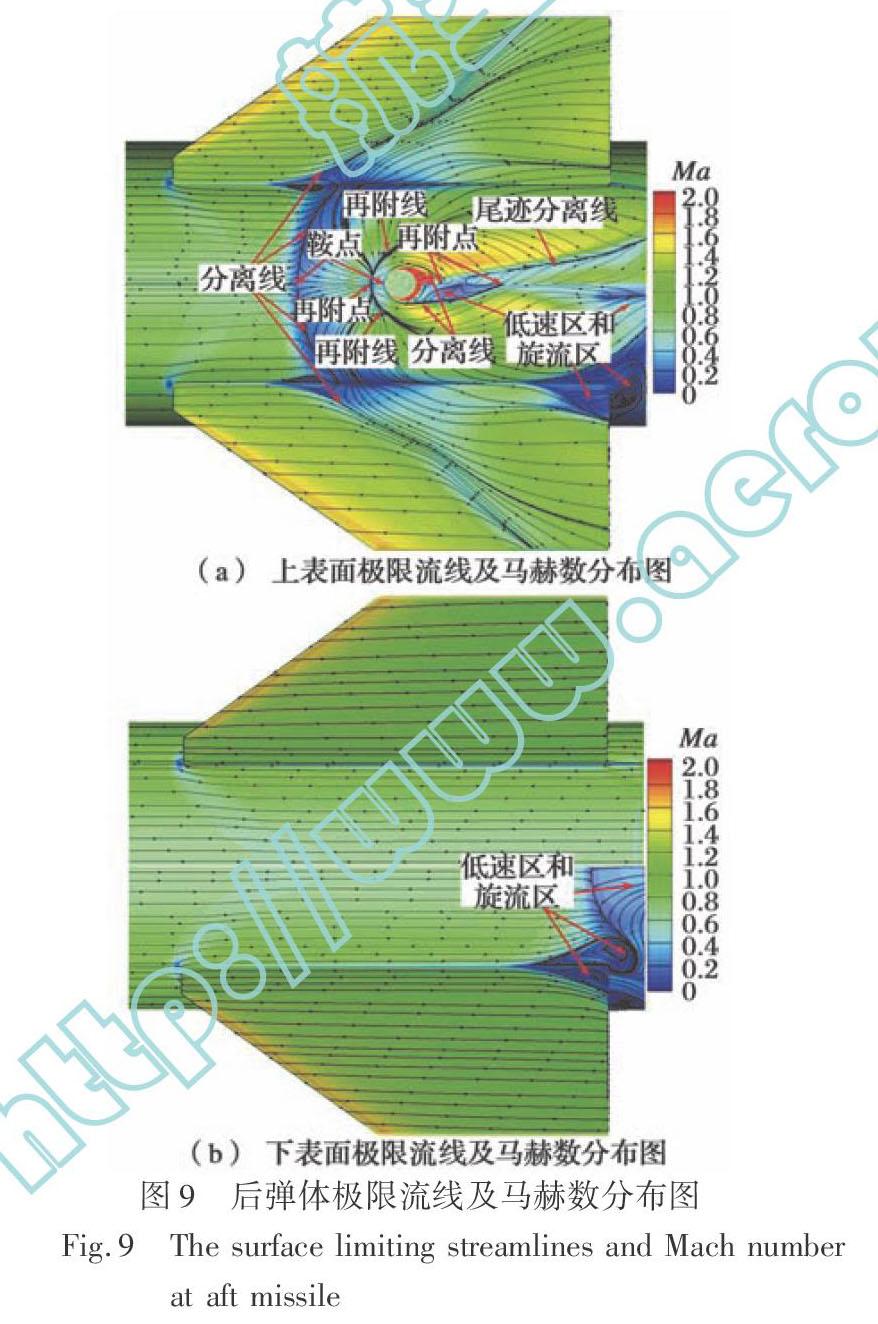
由于模型具有对称性，取弹体的一半进行网格划分，计算网格采用六面体结构化网格，为了确保壁面Y+在合适的范围内，经过多次试算，最终确定壁面第一层网格高度为0.1 mm，在压强变化比较剧烈的侧向喷口、舵片和后弹体附近进行了局部加密，网格总数分别为450万（无尾喷流状态）和520万（有尾喷流状态）。图2分别为计算域的整体网格和后弹体附近的局部网格。

1.2 计算条件

为了对比分析发动机尾喷流对侧向喷流干扰特性的影响，分别选取无尾喷流和有尾喷流两类计算状态，弹体攻角为0°。具体计算条件如表1所示，其中： P∞为主流静压;T∞为主流静温;Ma∞为主流马赫数;P*L为侧向喷流总压;T*L为侧向喷流总温;P*p为发动机尾喷流总压;T*p为发动机尾喷流总温。

1.3 计算模型

控制方程采用三维轴对称定常可压缩Navier-Stokes （N-S）方程组，具体表示为

E-Evx+F-Fvy+G-Gvz=0

式中： E，F和G为对流通量矢量;Ev，Fv和Gv为粘性通量矢量。

研究选用基于密度的求解器，采用标准κ-ε湍流模型和标准壁面函数分别计算高速区和近壁区域的流动，并使用二阶迎风格式对控制方程进行离散。

1.4 基本假设

导弹在空中飞行时，后弹体附近来流与尾喷流相互掺混干扰，再加上侧向喷流的作用，流动非常复杂，因此在计算时作如下假设：

（1） 不考虑尾喷流与大气的化学反应;

（2） 不考虑尾喷流中的粒子，假设尾喷流为纯气相流动;

（3） 侧向喷流与发动机尾喷流和主流具有相同的物性参数。

1.5 尾喷流计算模型验证

采用文献[20]中的实验模型进行尾喷流计算模型验证，实验模型由旋转体弹体和发动机组成，具体实验模型和计算条件见文献[20]。

将仿真计算得到的弹体表面、尾流轴线、x=197及x=204截面上的无量纲压强与文献[20]中的实验数据进行对比（如图3所示），数值计算

结果与实验结果吻合较好，证明本文采用的计算模型能够较好地模拟发动机尾喷流。

1.6 侧向喷流计算模型验证

采用参考文献[21]中的导弹喷流实验模型对本文的侧向喷流计算模型进行验证，实验模型由旋转弹体和“X”型尾舵组成，具体实验模型及实验条件见文献[21]。

图4为弹体表面压力系数对比，侧向喷口上游和下游的压力系数与实验数据符合较好，证明本文采用的计算模型能够较好地模拟侧向喷流附近的流动状态和压强变化。

2 计算结果及分析

2.1 弹体表面压强分布

图5为0°攻角时有/无尾喷流状态下的弹体表面压强分布云图。与无尾喷流状态相比，有尾喷流状态下，侧向喷口上游的弹体表面压强分布并无任何变化，但是由于尾喷流的影响，与弹体底部相邻的弹体尾端出现了局部高压区，侧向喷口下游附近的局部低压区压强也有所增大，并且尾舵根弦后缘也产生了局部高压区。

2.2 对称面马赫数及流线分布

图6为0°攻角时有/无尾喷流状态下的对称面流线

和马赫数分布。在马赫数分布方面： 首先，在与弹体底部相邻的弹体尾端，无尾喷流影响时，该区域的气流马赫数仍然在1.2以上，而有尾喷流影响时，该区域的气流马赫数非常低（低于0.4）;其次，在侧向喷口下游区域，无尾喷流影响时，该区域的气流马赫数在1.6～2.4，而有尾喷流影响时，该区域的气流马赫数最低达到0.4以下，最高也仅在1.2左右。在气流流线分布方面： 由于急剧膨胀的发动机尾喷流对主流和侧向喷流产生了一定的干扰，导致在侧向喷口下游区域形成了较强的旋流。

2.3 弹体表面压力系数对比

图7为0°攻角时有/无尾喷流状态下弹体上表面（侧向喷流一侧）压力系数曲线。与无尾喷流状态相比，由于尾喷流的干扰作用，有喷流状态下侧向喷口下游区域的压力系数出现了一定的升高，由于尾喷流无法影响到侧向喷口上游，因此在侧向喷口上游，两种状态下的弹体表面压力系数完全相同。

图8为0°攻角时有/无尾喷流状态下弹体下表面（无侧向喷流一侧）压力系数分布。与无尾喷流状态相比，有尾喷流状态下尾喷流的干扰流动作用十分明显，使得弹体下表面的压力系数急剧增大。

2.4 侧向力及力矩放大因子对比

表2为0°攻角情况下的侧向力和力矩放大因

子对比。由表可见，在0°攻角时发动机尾喷流的影响能够放大侧向喷流的效果，增大侧向力放大因子和力矩放大因子。

2.5 后弹体及侧向喷口附近流场结构对比

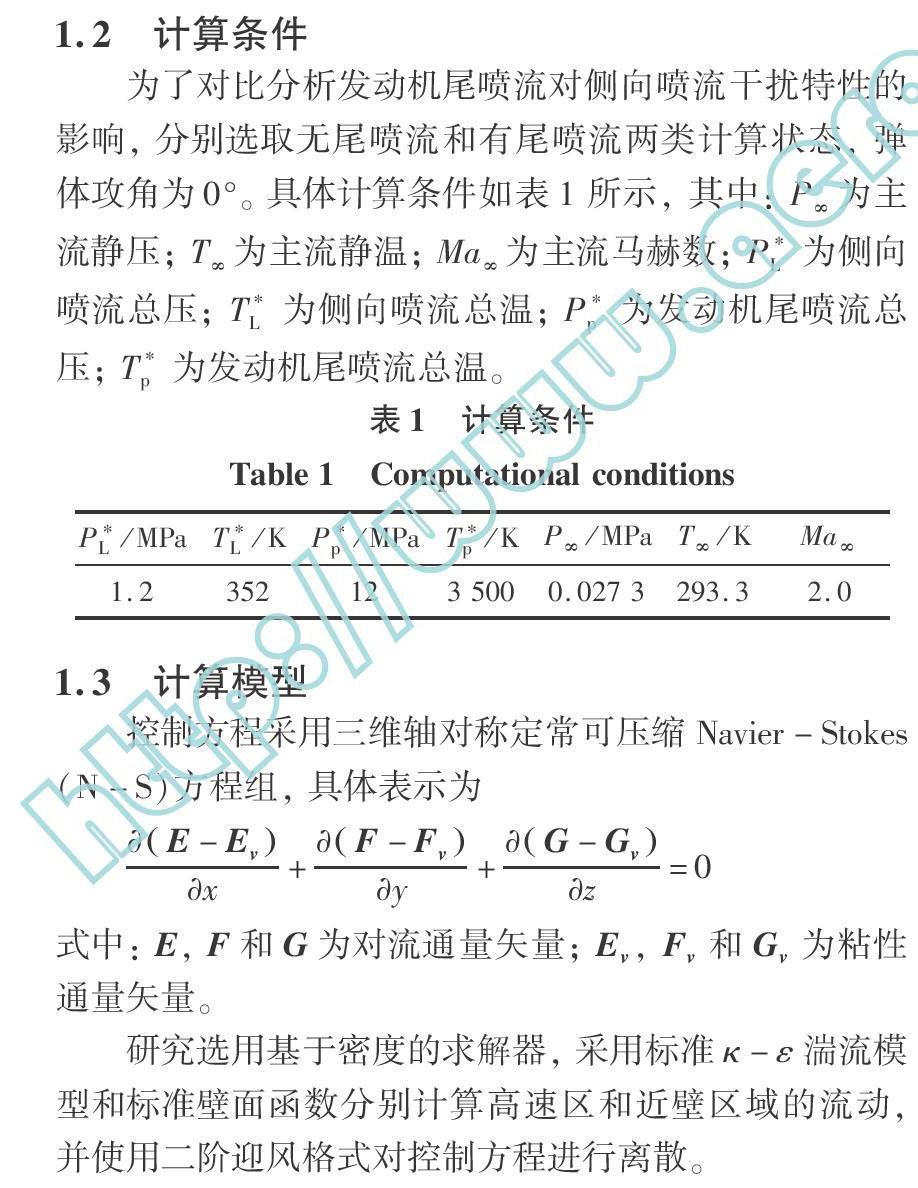
图9为有/无尾喷流状态的后弹体极限流线和马赫

数分布图（各图中上半部分為无尾喷流状态，下半部分为有尾喷流状态）。由图9（a）可见，在后弹体上表面侧向喷口上游区域，两种状态下的流线和马赫数分布相同，并且分离线、鞍点、再附点位置和再附线等流场结构也完全相同;而在侧向喷口下游区域，两种状态下的分离线、再附点、再附线和尾迹分离线等流场结构明显不同。与无尾喷流状态相比，有尾喷流状态的尾舵根弦后缘及其下游区域出现了大面积的旋流，形成了大面积的低速区，与侧向喷口相邻的下游区域也出现了部分旋流，并且低速区的面积也相应增大。由于这

几个旋流区的存在，造成了再附点更加远离侧向喷口，再附线更加偏向弹体对称面方向发展。由图9（b）可见， 在后弹体下表面的绝大部分区域，两种状态下的流线和马赫数分布都完全相同，但是由于发动机尾喷流的存在，使得有尾喷流状态的弹体底部附近和尾舵根弦后缘及其下游区域出现了大面积的旋流和低速区。

3 结论

针对采用尾端直接力装置的带尾舵尖拱头部-圆柱弹身导弹，本文采用三维复杂流场CFD仿真方法模拟了0°攻角情况下侧向喷流、尾喷流与主流的干扰流场特性，具体结论如下：

（1） 0°攻角时，发动机尾喷流与侧向喷流和主流的干扰会进一步增大弹体所受到的侧向力，放大直接力的效果;

（2） 从后弹体的流场结构和弹体表面压力系数分布来看，发动机尾喷流与侧向喷流和主流的干扰流动影响不到侧向喷口上游的流场结构、马赫数和压强分布，但是对侧向喷口下游的流场结构影响较大，继而影响后弹体及尾舵附近的马赫数和压强分布。

参考文献：

[1] 李斌， 王学占， 刘仙名. 大攻角侧向多喷干扰流场特性数值模拟[J]. 航空学报， 2015， 36（9）：2828-2839.

Li Bin， Wang Xuezhan， Liu Xianming. Numerical Investigation of Multi-Lateral Jets Interactions Flow Characteristics at High Angle of Attack [J]. Acta Aeronautica et Astronautica Sinica， 2015， 36（9）：2828-2839.（in Chinese）

[2] Hsieh T. Computation and Analysis of Cross Jet Interaction Flow-Fields of a Biconic Body at Incidences [C]∥ 16th AIAA Applied Aerodynamics Conference，Albuquerque，1998.

[3] Graham M J， Weinacht P， Brandeis J. Numerical Investigation of Supersonic Jet Interaction for Finned Bodies[J]. Journal of Spacecraft and Rocket， 2002， 39（3）： 376-383.

[4] 李亚超， 阎超， 张翔，等. 超声速横向喷流侧向控制的数值模拟[J]. 北京航空航天大学学报， 2015， 41（6）： 1073-1079.

Li Yachao， Yan Chao， Zhang Xiang， et al. Numerical Simulation of Lateral Control in Supersonic Cross Jet Flow[J]. Journal of Beijing University of Aeronautics and Astronautics， 2015， 41 （6）：1073-1079. （in Chinese）

[5] 马明生， 邓有奇， 郑鸣，等. 超声速侧向多喷流干扰特性数值模拟[J]. 空气动力学学报， 2007， 25（4）： 468-473.

Ma Mingsheng， Deng Youqi， Zheng Ming， et al. Numerical Investigation of Supersonic Jet Interactions for Tactical Bodies[J]. Acta Aerodynamica Sinica， 2007， 25（4）：468-473. （in Chinese）

[6] DeSpirito J. Factors Affecting Reaction Jet Interaction Effects on Projectiles[C]∥29th AIAA Applied Aerodynamics Conference，Honolulu，2011.

[7] Sahu J. Numerical Computations of Three Dimensional Jet Interaction Flow Fields[C]∥19th Atmospheric Flight Mechanics Conference， Scottsdale，1994.

[8] 杨磊， 叶正寅. 超声速飞行器侧向喷流干扰流场传统数值模拟方法的误差分析[J]. 航空动力学报， 2015， 30（10）： 2508-2515.

Yang Lei， Ye Zhengyin. Error Analysis of Lateral Jet Interaction Flow Field of Supersonic Vehicle with Traditional Numerical Method [J]. Journal of Aerospace Power， 2015， 30（10）： 2508-2515. （in Chinese）

[9] 孙得川， 由旭. 发动机引流推力矢量方案数值研究[J]. 推进技术， 2016， 37（3）： 436-442.

Sun Dechuan， You Xu. Numerical Research on Thrust Vector Control Scheme by Injection Bled from Motor [J]. Journal of Propulsion Technology， 2016， 37 （3）：436-442. （in Chinese）

[10] Brandeis J， Gill J. Experimental Investigation of Super-and Hypersonic Jet Interaction on Configurations with Lifting Surfaces[C]∥22nd Atmospheric Flight Mechanics Conference， New Orleans，1997.

[11] 孙得川， 杨建文， 白荣博. 喷流气体性质对导弹侧向喷流流场的影响[J]. 空气动力学学报， 2010， 28（6）： 720-723.

Sun Dechuan， Yang Jianwen， Bai Rongbo. The Effect of Gas Properties on the Lateral Jet Interaction Flowfield[J]. Acta Aerodynamica Sinica， 2010， 28（6）： 720-723. （in Chinese）

[12] Sourgen F， Gauthier T， Leopold F， et al. Substitution of Hot-Gas Lateral Jets by Cold-Gas Jets in Supersonic Flows[J]. Journal of Spacecraft and Rockets， 2011， 48（1）：81-92.

[13] 劉耀峰， 薄靖龙. 侧向喷流干扰流场建立与消退过程数值模拟[J]. 宇航学报， 2015， 36（8）： 877-884.

Liu Yaofeng， Bo Jinglong. Numerical Simulation of Establishment/Vanishment Process of Lateral Jet Interaction Flowfield [J]. Journal of Astronautics， 2015， 36（8）：877-884. （in Chinese）

[14] Sahu J， Fresconi F， Heavey K R. Unsteady Aerodynamic Simulations of a Finned Projectile at a Supersonic Speed with Jet Interaction[C]∥32nd AIAA Applied Aerodynamics Conference，Atlanta，2014.

[15] Batiuk G，Henderson J H. A Summary of Jet Plume Effects on the Stability Characteristics of a Body of Revolution with Various Fin Configurations at Mach Numbers from 0.2 to 2.3（Normal Jet Plume Simulator），US AMC RD-TR-76-2 [R]. Alabama： Redstone Arsenal， 1976.