小学低年级学生数学符号意识的培养策略
2020-07-16黄慧华
黄慧华
(建阳区实验小学,福建 南平 354200)
《义务教育数学课程标准(2011 年版)》(以下简称《课标》)明确指出:符号意识的使用有助于学生的数学表达和数学思考。数学符号是数学科学专门使用的特殊文字,是含义高度概括、形体高度浓缩的一种科学语言,是根据数学思维特点的需要而产生的理想化的科学书面语言。[1]数学符号意识的培养,有助于学生用数学符号的语言形式进行数学表达,并能运用符号进行“符号思考”,使学生具有数学特色的思维方式,渗透数学抽象、数学推理、数学模型等基本思想,所以数学符号意识的培养要从小学低年级抓起。笔者结合教学实践,从以下四点阐述如何培养小学低年级学生的数学符号意识。
一、在数学符号的抽象过程中,应用符号语言表达
数学符号的形成有一个抽象的过程,而数字符号是低年级小学生最早接触到的一种数学符号,随着年级的升高,学生还会认识关系符号、运算符号等。记录数量要用到数字符号,数字符号的抽象过程,要结合低年级的年龄特点,创设生活情境,借助已有经验,让学生在各种数学活动中亲历数字符号“直观到抽象、从具体到概括”的形成过程,并能运用这些数字符号进行数学活动。
例如:北师大版小学一年级数学在认识数字1时,教材中呈现了一个蕴含丰富的数学信息,表现了农村常见的生活场景。在问题串一“说一说,认一认”环节,让学生经历从多个实际背景不同但具有相同数量的情境中抽象数字符号“1”的过程,如1 个太阳、1 个萝卜、1 筐萝卜、1 棵树,它们都可以用1 来表示。学生体会到,像1 个萝卜这样的个体,可以用1来表示,而1 筐萝卜这样的一个集合,也可以用1 来表示;像1 棵大树这样很大的物体,可以用1 表示,像1 棵小草这样很小的物体,也可以用1 表示。在问题串二“数一数,认一认”环节,让学生经历类似的学习过程,抽象出“2”“3”“4”“5”。最后在问题串三“找一找,说一说”环节,鼓励学生根据给出的数,找出生活中相对应的物体数量的实例。这样设计的目的,实际上是“数表示物体的数量”的进一步理解和应用,也是抽象出数字符号的具体化的过程。
二、在寻找数字关联的过程中,引发符号思考
朱莉娅·安吉莱瑞指出:教师要让学生灵活熟练地运用数字,了解数字之间的关联,对所遇到的数字模式和计算过程做出归纳,并能把新知识与已有知识相联系。[2]低年级学生在认识较大的数字符号时,可以把这些数字进行有规律的排列。让学生理解某些符号出现的规则性,理解符号模式的逻辑结构,寻找数字间的联系,通过辨认数字模型来建构较大的数。[2]
例如:教学《做个百数表》一课时,根据百数表(见图1)的规律,学生不难发现百数表内的数字模式:(1)最大的数是100,最小的数是1。(2)同行的数,十位数字相同(整十数例外);相邻两数,右边的数比左边的数大,左边的数比右边的数小;(3)同列的数,个位数字相同;相邻两数,上面的数比下面的数小10,下面的数比上面的数大10。根据发现的数字模式与数字关系,不难填出图中所缺的数。寻找一个数与其他众多的数之间的关联需要靠数感,在巩固环节设计用△、○、□遮住百数表中的三个数,让学生说说这三个数分别代表什么数字。学生观察后得出:△在第4 行第3 列,表示33;○在第9 行第6 列,表示86;□在第6 行第10 列,表示60。学生的思维不再停留在直观的图形上,而能将具体化为抽象,理解图形所表示的含义。这样的感知过程,能够加强学生对于符号的认识,进行“符号思考”,明白符号可以表示不同的数,它与数字相联系,随时在变化,同时渗透了数对思想。
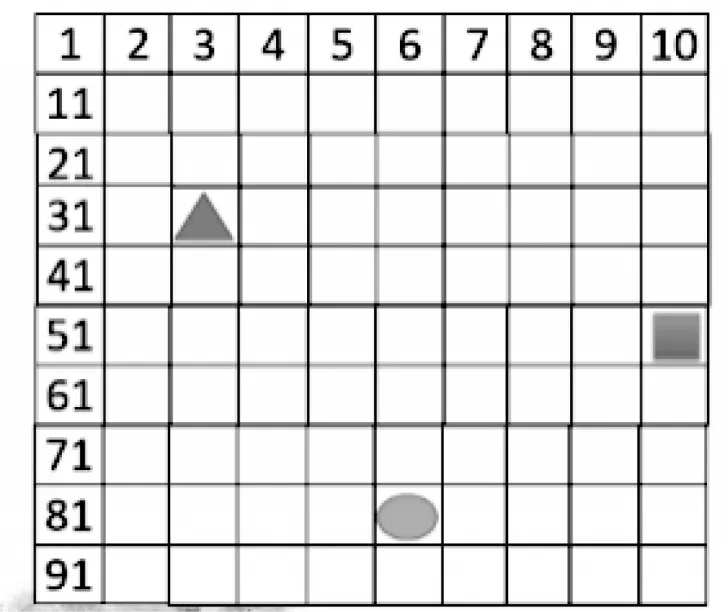
图1
三、在新旧知识的转化过程中,拓展符号的内涵
数学知识之间有很强的连续性和系统性。在小学数学教材中,大多数数学知识都有特定的起点,即新知的生长点。教师在钻研教材时,应把着力点放在新旧知识的连接点上,帮助学生经历由旧知向新知的转化过程,将转化思想方法渗透其中,发展学生的思维能力。[3]
例如:北师大版小学数学二年级上册《有多少张贴画》,这一课重点是利用旧口诀进行推算。推算6×7 的结果时,引导学生借助点子图进行推算,可以由6个6 加1 个6、5 个6 加2 个6、4 个6 加3 个6 得出答案。学生经历了先分后合的过程后,找到其中蕴藏的规律,接着在练习环节,可以设计有层次的拓展习题,拓展符号意识的内涵。如:
②△×3=18,△=( );
③6×A=6×3+6×5,A=( )。
前两题比较简单,学生很快就能得出结果。计算第三小题时,先引导学生明白“=”表示左边的A 个6 与右边的结果是相等的,“A”是数字的代替符号,再观察算式的两边都有相同的数字6。有了前面推算的经验,学生很快就能把右边的算式理解为3 个6 加5 个6,即8 个6。在这样的思维引导下,得出A 就是3与5 的和,即A=8。在小学低年级数学教学中,“=”这个数学符号是最常用到的,起到一种对等作用,要让学生主动去构建这样的观点,强化对这个符号的认识。再出示“8×B=8×4+8×4,B=( )”这样的习题,学生能很快地建构出“=”两边的结果一样,以及“B”是代表数字的数学模型,得出B 是4 与4 的和,即B=8。
四、在探索变化规律的过程中,提升符号素养
课标明确提出,要运用符号表示数、数量关系和变化规律,这也是培养和发展学生数学符号意识的最终目的。如在教学北师大版小学数学一年级上册《做个加法表》时,教师在最后的练习环节,出示下面一组由浅入深的阶梯式练习,如6+△=8,7+△=( ),8+△=( ),用△(也可用苹果、字母等符号代替)表示相同不变的数,让学生明白还可以根据算式之间的规律(两数相加,其中一个加数不变,另一个加数加几或减几,和也跟着加几或减几)进行灵活计算,从而培养数感、符号意识、代数思维等。教学《做个减法表》一课时,也可以用这种方法培养符号意识。
数学符号意识培养的过程,也是一个抽象、概括、观察、分析、判断、推理等能力培养的过程。教学时,要利用各种方法,以及学生原有的知识结构和生活经验,帮助学生主动构建符号意识,积极引导学生主动回顾,理解符号的意义并能灵活运用符号,准确把握符号意识的内涵与本质,建立科学的符号意识观,丰富学生的数学素养,在运用中强化符号意识,促进学生的思维发展,引发学生的“符号思考”。
