基于ADAMS的动车组齿轮箱断齿故障特征研究

2020-07-16高国川张建超郭文武夏子阳

国防交通工程与技术 2020年4期

高国川, 张建超, 郭文武, 夏子阳

(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043；2.石家庄铁道大学机械工程学院，河北石家庄 050043)

齿轮箱作为动车组列车传递动力的重要部分，一旦发生故障将对动车组的安全运行产生严重影响。相关资料显示[1]，齿轮箱中齿轮发生断齿故障所占比例最大，故对齿轮故障信号特征进行研究具有重要的实际应用意义，能够在故障发生初期实现预判，避免事故的发生。

目前对动车组齿轮箱的故障监测主要为温度监测[2]，该种监测方法不能及时地监测出齿轮的故障；在齿轮箱的定检中，多数学者采用强度分析法、金相组织分析法、磁粉探伤法对断齿故障进行检测[3-5]，但不能对齿轮进行实时的故障监测；何斌斌提出采用振动监测的方式对齿轮箱进行故障诊断[6]，但由于试验条件的限制，未能在短时间内采集到大量的振动信号数据；刘丽基于Lab View软件建立了高速列车牵引传动系统的监测与预警系统平台[7]，该平台中信号特征的评价指标相对较少，不能及时地监测出齿轮是否发生故障；林新海[8]采用模态试验和台架试验相结合的方法研究动车组齿轮箱的振动特性，结果表明齿轮箱的振动在变工况的条件下受转速影响较大，但未对齿轮箱发生故障时的振动信号特征进行分析。

随着虚拟样机仿真技术的发展成熟[9-10]，可以通过建立齿轮箱的动力学模型并进行接近实际的仿真，得到正常和含有故障时箱体的信号数据，分析总结出信号特征。为研究动车组齿轮箱发生断齿故障时箱体的振动信号特征，本文将建立齿轮箱的动力学模型，基于ADAMS动力学软件对正常齿轮和断齿齿轮进行仿真，采用振动检测方法得到箱体某测点振动信号，并以正常齿轮运行时箱体振动信号为基准，对比分析断齿故障时振动信号的时频域特征，为动车组齿轮箱的状态监测和故障预判提供参考。

1 动力学建模

以某型号动车组齿轮箱为研究对象，以实物箱体为基础在SolidWorks软件中建立上下箱体的三维模型，装配时以直接绑定的形式代替上下箱体之间的螺栓连接，将上下箱体视作一个整体。根据表1中参数建立大小齿轮的三维模型，然后装配到箱体装配体中，并调用Toolbox中的轴承来完成箱体整体结构的装配。本文所研究齿轮箱为一级减速传动，小齿轮转速较快，故小齿轮发生故障概率相对大齿轮而言较大。本文在小齿轮的某齿上预先设置了断齿故障如图1所示。

柔性箱体可以更为准确地反映出箱体受到冲击后的振动信号特征[11]，故本文通过ANSYS有限元软件对箱体进行柔性化处理，生成柔性箱体，然后在ADAMS软件中建立传动系统刚性、箱体柔性的刚柔耦合动力学模型并对正常齿轮和断齿齿轮进行仿真。

表1 齿轮参数表

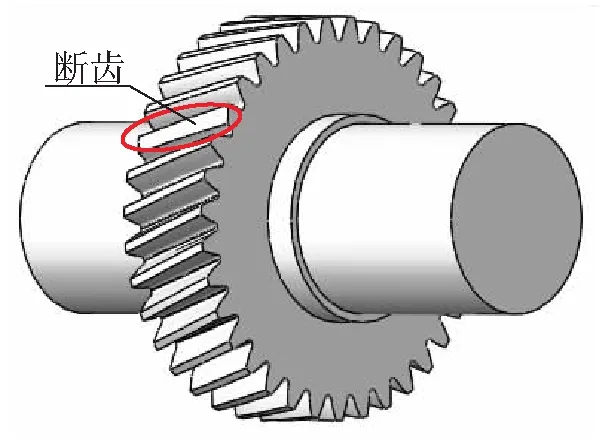
图1 断齿齿轮模型

将箱体模型导入到ANSYS软件中，定义好实体单元材料和质量单元属性后对其进行划分网格，然后创建刚柔耦合模型中刚性体和柔性体连接处的刚性区域，最后输出包含构件模态信息的柔性箱体文件。将齿轮箱装配体模型导入到ADAMS软件中定义好各个构件的材料属性，用生成的柔性箱体替换掉模型中的刚性箱体，根据箱体在实际中的安装方式[12]，设置好柔性箱体与其它刚性体之间的约束，即可生成齿轮箱的刚柔耦合模型，如图2所示。

图2 齿轮箱刚柔耦合模型

2 参数的设定

2.1 接触力参数的设定

齿轮发生断齿后参与啮合时会使啮合力发生突变，产生一定的冲击，导致箱体振动信号发生变化，故仿真前准确设置计算啮合力所需参数可以使仿真过程更加接近实际。

ADAMS中设有建立齿轮副和添加碰撞接触力两种模拟齿轮啮合传动的方式，用建立齿轮副模拟的啮合传动是理想的齿轮副传递过程，但是不能反映出啮合力等动力学特性；用碰撞接触力形式模拟的传动系统，可以通过设置接触刚度和力指数等参数更好地反映出齿轮的啮合过程。本文拟分析箱体的振动信号，故采用添加碰撞接触力的形式来模拟齿轮的啮合传动，并选用其中的“冲击函数法”以计算齿轮啮合时的接触力，即啮合力。冲击函数法中各个参数的设置如下：

(1)接触刚度系数K。K值的大小与接触面的形状和物体的材料属性相关，由Hertz接触理论，计算公式为：

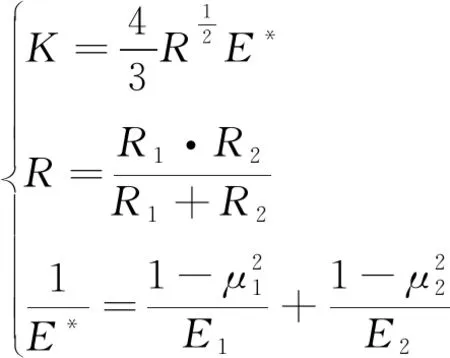
(1)

式中：R1、R2分别为齿轮啮合点的当量半径；E1、E2分别为齿轮材料的弹性模量，E1=E2=2.07×1011Pa；μ1、μ2分别为齿轮材料的泊松比，μ1=μ2=0.29。代入相关数据，求得本文K值为 1.29×106。

(2)接触指数e。用以反映材料的非线性程度，根据Hertz理论，本文e值取1.5。

(3)阻尼系数C。用以反映物体碰撞时的能量损耗，根据经验和反复试验，本文C值取10。

(4)切入深度d。设置过大则啮合过程中发生真正的切入，设置过小则使计算结果偏大，根据经验和反复试验，本文d值取0.1 mm。

(5)参考相关文献[13]并结合齿轮材料属性和润滑情况，库伦摩擦力的相关参数取值如下，动摩擦系数μd取0.05，动滑移速度vd取10 mm/s，静摩擦系数μs取0.08，静滑移速度vs取1 mm/s。

2.2 仿真参数的设定

在动车组齿轮箱的实际安装结构中，小齿轮轴通过联轴器与牵引电机相连，故本文在小齿轮轴上添加step函数控制旋转驱动；大齿轮轴直接固定在车轮上，故在大齿轮轴上添加step函数控制负载扭矩。step函数可以较好地模拟出列车启动和运行过程中齿轮转速的变化，也可以避免负载扭矩发生突变。

上箱体大齿轮轴承座处既承受大齿轮轴传递的冲击，又承受一部分小齿轮轴对箱体的冲击；轴承作为齿轮轴和箱体的连接构件，轴承座处的振动信号具有一定的代表性。综合以上内容，加之本文拟测量箱体在垂直方向的振动加速度信号并结合相关文献[14]，本文最终在箱体大齿轮轴承座处设置一测点，用于测试箱体的振动加速度，测点具体位置如图2中标记所示。

仿真时模拟列车在250 km/h的速度下运行，对应的小齿轮转速为3 500 r/min，理论啮合频率为2 041.66 Hz；为了使系统保持平衡状态，负载转矩大小设置为3 800 N·m。经过换算，最终的旋转驱动函数为：step=(time,0,0,0.1,-21 000 d)，负载扭矩函数为：step=(time,0,0,0.1,-3 800 000)。

箱体受到的齿轮啮合激励为高频激励，为了更加准确地获取箱体振动信号，需要采用较高的采样频率；在ADAMS软件中，相同仿真时间内仿真步长设置得越小，输出的仿真结果次数越多，代表采样频率越高。综上所述，本文仿真时间设为0.5 s，步长设为0.000 1 s。

3 结果分析

分别对正常齿轮和断齿齿轮进行仿真，提取出箱体测点垂直方向的振动加速度信号，在MATLAB软件中采用振动信号处理方法，分别对正常齿轮和断齿齿轮的箱体振动信号进行时域和频域的分析，总结出齿轮发生断齿故障时振动信号的特征，为齿轮箱的状态监测和故障预判提供参考。

由于在仿真过程中，0.1 s后大小齿轮的转速才达到稳定状态，齿轮箱的运行也接近平稳，故本文中令时域图的时间从0.1 s开始。

3.1 时域分析

正常齿轮、断齿齿轮运行时箱体振动信号时域图如图3所示。

对图3进行分析得知，正常齿轮运行时，信号时域图中的振幅较小，放大后波形具有周期性，没有产生冲击信号，齿轮箱的整体运行较为平稳；将断齿故障信号与正常齿轮信号进行对比，发现时域图中的振幅有明显的增大，而且产生了周期性冲击，0.4 s内冲击信号出现了22次，换算后与小齿轮理论转频(58.3 Hz)十分接近，表明齿轮发生断齿故障后对箱体产生了冲击，破坏了齿轮箱的平稳运行。

为了对时域信号进行更为深入的研究，提取了时域特征量中的峰值、平均幅值、峰值因子、峭度因子和脉冲因子5种指标对信号进行评测，各种指标见表2。其中，峰值因子和脉冲因子均是用来检测信号中有无冲击的指标，峭度因子也用来反映信号的冲击特性。

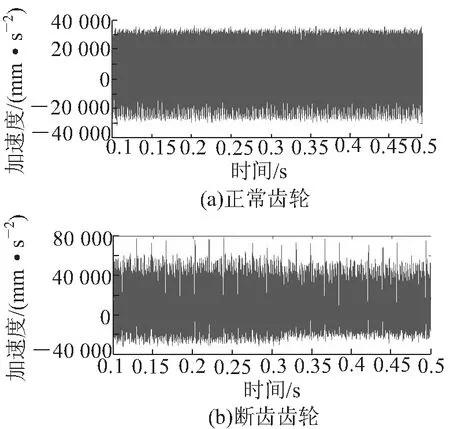
图3 箱体振动信号时域图

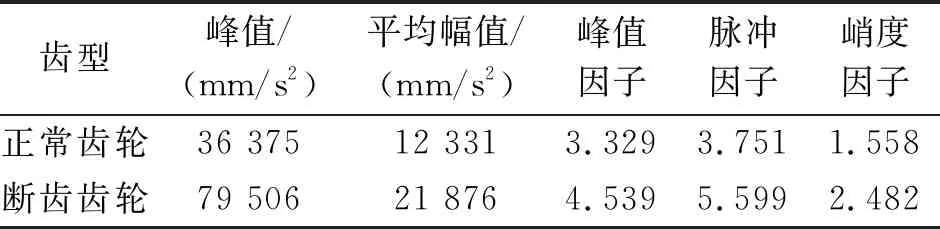
表2 不同齿轮的信号时域特征表

对表2中数据进行分析得知，齿轮发生断齿故障后，振动信号的峰值和平均幅值均有明显的增大，峰值因子、脉冲因子和峭度因子均有一定的增大，表明产生了一定的冲击。上述结论与由时域图所得结论相符，进一步增强了本文所得的断齿故障特征的可信度。

3.2 频域分析

正常齿轮、断齿齿轮运行时箱体振动信号频域图如图4所示。

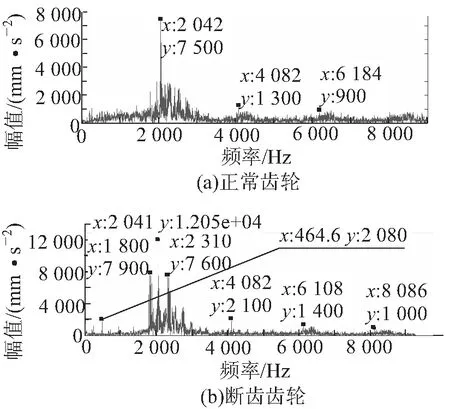
图4 箱体振动信号频域图

对图4进行分析得知，正常齿轮运行时，频域图中在2 042 Hz处振动幅值达到最大，与齿轮理论啮合频率2 041.66 Hz相差甚小，在约为啮合频率的2倍频和3倍频处幅值迅速减小，表明箱体主要以齿轮的啮合频率振动；虽然在啮合频率附近出现了幅值较小的小范围调制边频带，但处于齿轮正常运行时允许产生的调制范围内。

将断齿故障信号与正常齿轮信号进行对比，发现频域图中的振幅有明显的增大，2 041 Hz处的幅值最大，464.6 Hz、4 082 Hz和6 108 Hz处幅值与附近幅值相比较大；464.6 Hz约为小齿轮理论转频的8倍频率，2 041 Hz十分接近齿轮的啮合频率，4 082 Hz和6 108 Hz约为啮合频率的2倍频和3倍频，由此可见齿轮发生断齿故障后会在小齿轮转频的高倍频率、齿轮啮合频率及其倍频附近出现宽且幅值较大的调制边频带。

为了更为深入地研究故障特征，采用Zoom-FFT法对该振动信号进行细化处理，通过希尔伯特变换解调法对振动信号进行解调处理，其细化谱如图5所示，解调谱如图6所示。

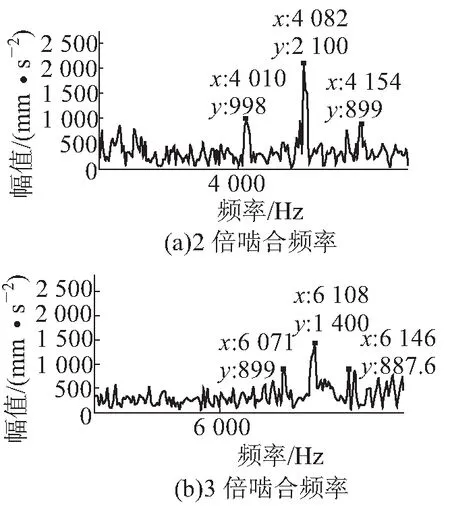
图5 断齿齿轮箱体振动信号细化谱

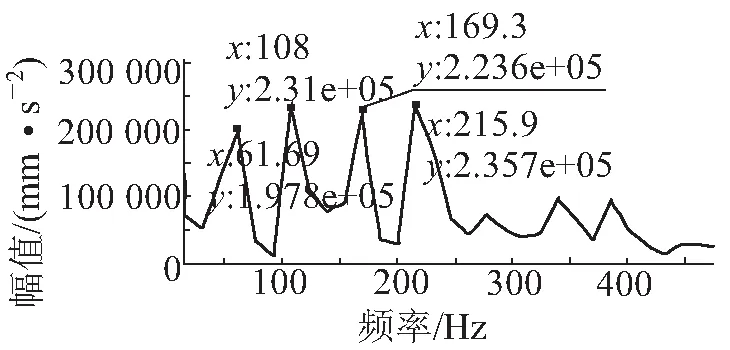
图6 断齿齿轮箱体振动信号解调谱

对图5进行分析得知，验证了断齿后会产生以啮合频率及其倍频为载波频率的调制现象，同时会引起较大的冲击，故调制的边频带较宽且幅值较大；对图6进行分析得知，解调谱中在61.69 Hz、108 Hz、169.6 Hz、215.9 Hz处幅值较大，频率值与小齿轮的理论转频及其高倍频率较为接近，解调后这些频率处有峰值出现，表明齿轮发生了故障。

综上所述，在对齿轮箱进行故障预判和状态监测的过程中，若发现振动信号出现上述特征，可初步判断齿轮发生了断齿故障，应调整动车组运行策略来降低齿轮箱事故的严重性。