Random Low Patch-rank Method for Interpolation of Regularly Missing Traces
2020-07-16JianweiMa
Jianwei Ma
(Department of Mathematics, Center of Geophysics and Artificial Intelligence Laboratory, Harbin Institute ofTechnology, Harbin 150001, China)
Abstract: Assuming seismic data in a suitable domain is low rank while missing traces or noises increase the rank of the data matrix, the rank-reduced methods have been applied successfully for seismic interpolation and denoising. These rank-reduced methods mainly include Cadzow reconstruction that uses eigen decomposition of the Hankel matrix in the f-x (frequency-spatial) domain, and nuclear-norm minimization (NNM) based on rigorous optimization theory on matrix completion (MC). In this paper, a low patch-rank MC is proposed with a random-overlapped texture-patch mapping for interpolation of regularly missing traces in a three-dimensional (3D) seismic volume. The random overlap plays a simple but important role to make the low-rank method effective for aliased data. It shifts the regular column missing of data matrix to random point missing in the mapped matrix, where the missing data increase the rank thus the classic low-rank MC theory works. Unlike the Hankel matrix based rank-reduced method, the proposed method does not assume a superposition of linear events, but assumes the data have repeated texture patterns. Such data lead to a low-rank matrix after the proposed texture-patch mapping. Thus the methods can interpolate the waveforms with varying dips in space. A fast low-rank factorization method and an orthogonal rank-one matrix pursuit method are applied to solve the presented interpolation model. The former avoids the singular value decomposition (SVD) computation and the latter only needs to compute the large singular values during iterations. The two fast algorithms are suitable for large-scale data. Simple averaging realizations of several results from different random-overlapped texture-patch mappings can further increase the reconstructed signal-to-noise ratio (SNR). Examples on synthetic data and field data are provided to show successful performance of the presented method.
Keywords: seismic data interpolation; low-rank method; random patch; geophysics
1 Introduction
Interpolation of missing traces is a critical stage in seismic data processing workflow. It is not only used to remove sampling artifacts but also to improve amplitude analysis. Many methods have been proposed for the seismic data interpolation. Wave-equation based methods need the wave propagation simulation to reconstruct seismic data, so a precise subsurface velocity model is required. Signal-processing based methods use sparse transforms to construct the data such as the Radon transform[1], Fourier transform[2-8], curvelet transform[9-12], seislet transform[13], and data-driven tight frame[14-15]. Another popular technique in the signal-processing based method is to use prediction filters[10,16-20]. The low-frequency non-aliased components of the observed data are applied to design anti-aliasing prediction-error filters, and then the filters are used to reconstruct high-frequency aliased components. This strategy makes the prediction filters suitable for interpolating linear events with regularly missing traces.
In the past few years, rank-reduced methods have been applied to seismic data reconstruction. These methods mainly fall into two categories: the Cadzow method and nuclear-norm minimization (NNM). The motivation of the Cadzow method is that a Hankel matrix constructed using a frequency slice of the data in f-x(frequency-spatial) domain, should be low rank. Trickett et al.[21]presented a truncated singular value decomposition (SVD) based matrix-rank reduction of constant-frequency slices. Oropeza and Sacchi[22]presented a multichannel singular spectrum analysis (MSSA) for simultaneous seismic reconstruction and random noise attenuation. The MSSA rebuilds seismic data at a given temporal frequency into a block Hankel matrix, and then introduces the projection onto convex sets (POCS) algorithm with a randomized SVD to reduce the matrix rank. Gao et al.[23]proposed a fast pre-stack seismic volume reconstruction method by applying Lanczos bidiagonalization. Naghizadeh and Sacchi[24]proposed multidimensional de-alised Cadzow reconstruction of seismic records by combining Cadzow reconstruction with Spitz's prediction filtering. More recently, Cheng et al.[25]proposed a computational efficient MSSA for pre-stack seismic data reconstruction.
On the other hand, seismic data interpolation can be formulated as an NNM problem[26-27]. This is based on the sparsity regularization of matrix singular values. Yang et al.[26]first designed a pre-transformation, the so-called texture-patch mapping[28], to reorganize the data into a texture-patch matrix of low rank, then applied a fast NNM algorithm to recover the low-rank matrix. Ma[29]extended the NNM matrix completion (MC) for three-dimensional (3D) irregular seismic data reconstruction. Recently, Yao et al.[30]applied the texture-patch based method in the f-x domain. Kumar et al.[31]applied a coordinate transformation from source-receiver domain to midpoint-offset domain, and then used the NNM MC algorithm for the m-h data frequency by frequency in the f-k (frequency-wave number) domain, Aravkin et al.[32]presented a robust SVD-free approach to MC. In comparison with the f-x domain Hankel matrix based Cadzow methods, the NNM MC algorithm is faster and can deal with larger-scale data[26]. Applications of rank-reduced methods (specially named tensor completion) for 4D and 5D seismic data interpolation have also been implemented[23,33-36].
Generally speaking, sparse-transform based methods mainly capture large magnitude components and ignore small magnitude components for high-frequency band. Most of them are local methods. However, the NNM methods mainly capture the patterned components (because of the relatively large singular values), and ignore the small singular values described by non-pattern components. The Hankel matrix based rank-reduced methods assume a superposition of linear events for seismic data. In this case, multidimensional data embedded in a Hankel matrix form a low rank matrix with a rank that is equal to the number of dips in the data[37]. Our patch low-rank method has less stringent constraints on curvature and linear events[26,29]. It is assumed that seismic data consist of repeated texture patterns. In this case, the data after the patch mapping lead to a low rank matrix. Thus, the patch low-rank methods can cope with the problem that waveform dips vary in space.
According to MC theory, any columns (and any rows) of the observed matrix must be required to have at least one non-zero entry, to achieve successful reconstruction. However, the interpolation of missing traces will lead to a higher matrix rank rather than a lower matrix rank, which is opposite to the basic requirement of low-rank MC. Thus, the seismic data cannot be directly interpolated successfully because "zero" columns are resulted from the missed traces. A pre-transform or mapping needs to be designed. To make the MC theory work, the new matrix in the transform domain should have lower rank, and more importantly, the missing traces should increase the rank of the new matrix.
The texture-patch mapping suggested in Ref.[26] avoids such zero columns in the new matrix. After the texture-patch transform, the missing traces in observed data are shifted with zero pixels in the new matrix. The missed pixels increase the rank of matrix. Generally, for seismic data consisting of texture components (events), the texture-patch mapping leads to lower rank[28]. In fact, for the Cadzow method, the Hankel matrix in the f-x domain can be also seen as a pre-transformation, which makes the rank-reduced method suitable for seismic data interpolation.
However, the previous method presented in Refs.[26,29] does not work for interpolation of regularly missing traces. Because the regularly missing traces in seismic data often lead to aliasing the in f-k domain, these data are referred to as aliasing data. Using the suggested patch mapping method in Refs.[26,29], the new matrix after the texture-patch mapping is applied to aliasing data that still include "zero" rows. That is to say, the mapping transforms the "zero" columns to "zero" rows instead of expected distributed "zero" pixels.
The challenge motivating this paper is how to make the low-rank methods work for aliased data without additional prediction techniques. To solve this key problem, a 3D random overlapped texture-patch transform was designed, which maps the 3D sub-blocks into column vectors that compose a new low-rank matrix. Then a low-rank factorization matrix fitting method (so-called LMaFit) and an orthogonal rank-one matrix pursuit (OR1OMP) method[38]were applied to efficiently solving the presented patch low-rank MC. The method presented in the paper may not replace current state-of-the-art methods for interpolation of seismic data, but can offer a new perspective on the problem.
Recently, machine learning methods have also been applied for seismic data interpolation[39-42]. Discussion of the learning based methods is beyond the scope of this paper.
2 Theory
2.1 Random-Overlapped Texture-Patch Mapping
A seismic data interpolation problem can be considered as
Y=PΩ(X)
(1)
whereXdenotes original data that is to reconstruct,Ymeans the observed or corrupted data, andPΩstands for trace sampling.
(2)
wherePΩ(X) is zeros at the locations of missing traces, and Ω is index subsets for sampling traces. The missing traces inXdecrease the rank of matrixX, i.e., the rank ofYis lower than the rank ofX. Thus,Xcannot be reconstructed via the classic low-rank method. In Refs. [26, 29], the non-overlapped texture-patch mapping was considered for the randomly missing traces. In this paper, for the regularly missing traces, a random overlapped texture-patch mapping was designed.
The 3D random-overlapped texture-patch mapping,T∶Mn,m,q→Mnmqα/r3, is defined as follows: for av∈Mn,m,q, partition upvintor×r×rsubblocks, labeled as {Bi}i=1,…,nmqα/r3.αindicates an overlapping factor. Each subblock is randomly shifted to the original of coordinatesδ:=(δx,δy,δt), where theδx,δy,δtdenote shift step numbers inX,yandtdirections, respectively. In this paper,δx,δy∈(0,1,2,3,4,5) andδt=0 are taken. That is to say, for the neighbor subblocks, they may have overlapping no more than 5 columns/rows in two spatial directions. EachBiis rearranged into a column vectorwiof lengthr3following the same ordering. Thus the new matrix is formatted as
(3)
As mentioned in Ref. [28], the texture-patch mapping reduces the nuclear norm of 2D matrices for texture images, ‖TX‖*≪‖X‖*.For the 3D case, ‖Tv‖*≪‖v‖*, in which ‖v‖*is defined by the trace norm of the tensor[43].
Fig.1 is an illustration of the random-overlapped texture-patch mapping.
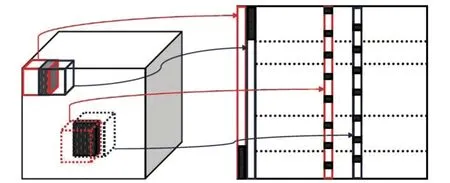
Fig.1 Illustration of random-overlapped texture-patch mapping from 3D volume to 2D matrix
that dataXof size 4×4×2 are mapped into a new matrix by a 2×2×2 patch.

(4a)
(4b)
(5)
One column overlap is used between the first and second block (i.e.,δx=1,δy=0,δt=0), and another column overlap between the second and third block. Due to the overlapping, dataXare partitioned into 5 subblocks, and after the mapping a new matrix of size 8×5 is obtained. In the illustration, how the elements move can be easily seen. The repeated elements resulted from overlapping will be averaged in the reconstruction. It should be noted that the method guarantees that the rank is decreased only for texture-pattern data after the texture-patch mapping. It models texture-like seismic components as an alignment of patches, which are almost linearly dependent. Thus low-rank promoting NNM can be used to reconstruct the texture-like events.
A synthetic 3D data with dimensions 128×128×128 that will be used in example section is taken as an example here. Fig. 2 shows the singular value plot for original dataX(dot-dashed line),Xwith regular subsampling (dashed line), andXwith random subsampling (solid line). Both subsampling patterns decrease the rank of matrix, thus the classic low-rank method cannot be used to directly reconstructXfrom its subsampling data.


Fig. 2 Singular values plot with decreasing amplitude for one section of a synthetic seismic data(The dot-dashed line corresponds to original data X as shown in Eq. (1); the dashed and solid lines correspond to X with regularly missing traces and randomly missing traces, respectively; both subsampling patterns decrease the rank of matrix)

Fig. 3 Singular value plot for with 50% randomly missing traces (The dot-dashed line corresponds to original data after non-overlapped mapping; the dashed and solid lines correspond to the subsampling data after non-overlapped mapping and random-overlapped mapping, respectively.)

It is also worth noting that the amplitude of singular value of randomly overlapped mapping is smaller than the original when the amplitude is large. In experiments, it does not affect the final results. The main concern of this paper is the decay of curves, i.e., how many non-zero significant singular values does it have after a thresholding. But that will be addressed in the next work.
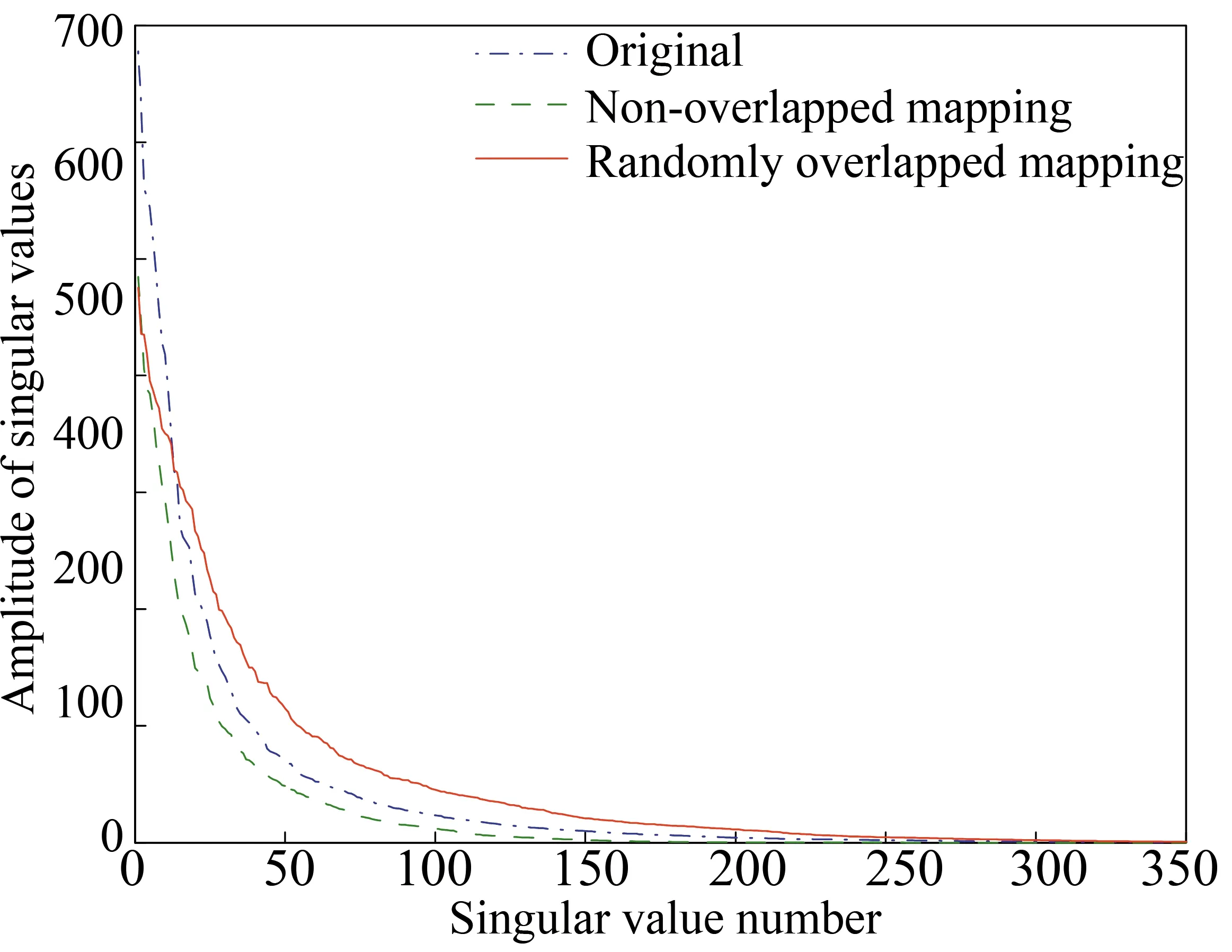
Fig. 4 Singular value plot for with 50% regular missing/subsamping traces (The dot-dashed line corresponds to original data after Non-overlapped mapping; the dashed and solid lines correspond to the subsampling data after Non-overlapped mapping and random-overlapped mapping, respectively.)
2.2 Low Patch-Rank Model and Algorithm

(6)
Suddenly, I heard voices. I glanced around and saw at least eight high-school-age boys following me. They were half a block away. Even in the near darkness I could see they were wearing gang insignia.
For efficient computation, its relaxation version is often considered:
(7)
(8)
where the R-norm ‖X‖R=‖TRX‖*, andTRdenotes the random-overlapped texture-patch mapping. As put forward by the theory of MC, suppose one observesmentries selected uniformly and randomly from a matrix of sizen×n, then most low-rank matrices can be completed by solving a simple convex optimization problem, if the numbermof sampled entries obeysm≥Cn1.2rlogn. HereCdenotes a positive numerical constant, andrdenotes the rank of the matrix.
Most rank-reduction algorithms require SVD in each iteration, which is the main computational cost for large-scale problems. In order to avoid the SVD computation in solving the NNM model, the low-rank factorization model[46]is applied.
(9)
The motivation is that any matrixX∈Rm×nof a rank up toκhas matrix factorizationX=AB, whereA∈Rm×κandB∈Rκ×n. Here variableZ∈Rm×nis introduced for a computational purpose, andκis a predicted rank bound that will be dynamically adjusted. With an appropriateκ, this low-rank factorization model provides results very close to the NNM model[46].

(10)
(11)
The above equation can be reformulated as
(12)
The model shown in Eq. (12) can be solved by an orthogonal-matching-pursuit (OMP) type greedy algorithm using rank-one matrices as the basis. It is a natural extension of OMP from previous vector case to the matrix case. The detailed algorithm is provided in the appendix.
3 Examples
In our experiments, the maximum overlap is taken as 5 (i.e., the overlap will be a number randomly chosen from {0,1,2,3,4,5}) in the spatial directions. The proposed algorithm was first tested on synthetic 3D data with dimensions 256×32×32 and four linear events.
Fig. 5(a) shows the original data, and Fig. 5(b) shows the corrupted data with approximately 50% regularly missing traces (section subsampling inxdirection). Fig. 5(c) is the reconstruction and Fig. 5(d) is the difference between the reconstruction and original data. In order to demonstrate how the amplitude is reconstructed, the centert-xsection by waveform display is shown in Fig.5(e). The left part is the original data and the right part is corrupted data. Fig.5(f) shows the reconstruction and its reconstruction errors (difference between the reconstruction and original data).

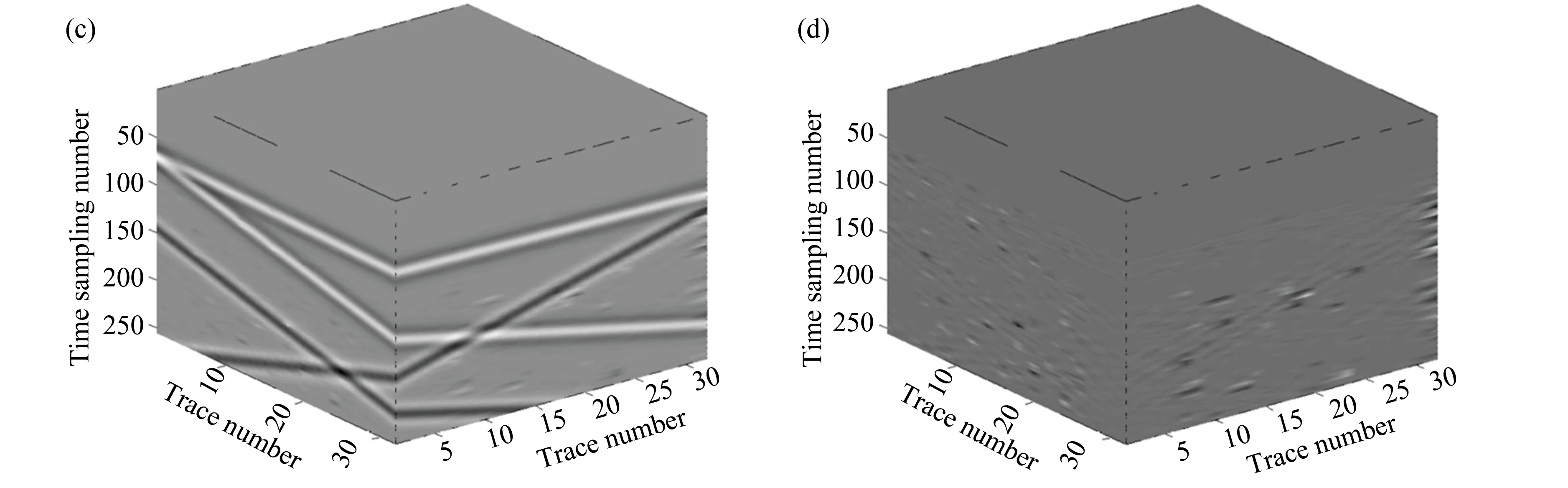

Fig. 5 (a)Original data;(b) Corrupted data with 50% regularly missing trace;(c) Reconstructed data, signal-to-noise ratio(SNR)=16.32;(d) Difference between the reconstruction and original data;(e-f) Waveform display of a center section for original data, corruption, reconstruction, and difference, respectively
Fig.6 displays the trace comparison. The dashed line is the original trace that was missed, and the solid line is the reconstructed trace. The amplitude of the trace is kept well except for some slight artifacts.
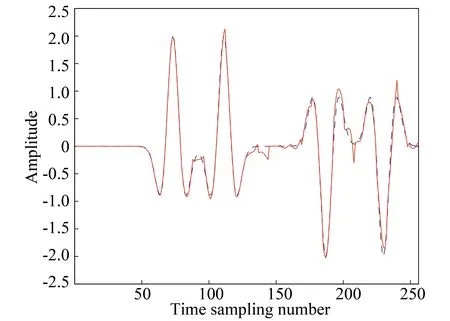
Fig. 6 A central trace comparison (The dashed line denotes the original trace that was missed; the solid line denotes the reconstructed trace.)
In Fig. 7, a simulated 3D data with dimensions 128×128×128 was tested . The center slices in three directions of the 3D volume are displayed. From the top row to the bottom row, the original data, corruption, reconstruction, and the error are shown. The reconstruction performance is satisfied in this case.The result presented in Fig. 7(g) may not look so good. This is because the profile/section in Fig. 7(g) is totally missed as shown in Fig. 7(d). It should be interpolated from other sections. Fig. 8 displays the f-k spectra of the original data, corruption, and the reconstruction. Most f-k aliasing resulted from regularly missing traces are suppressed by the proposed method.
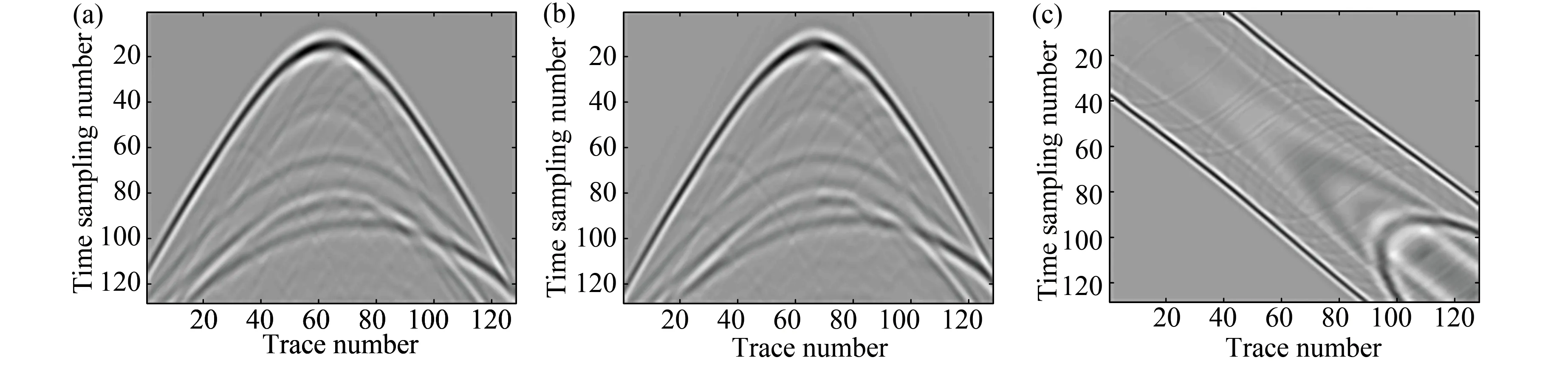

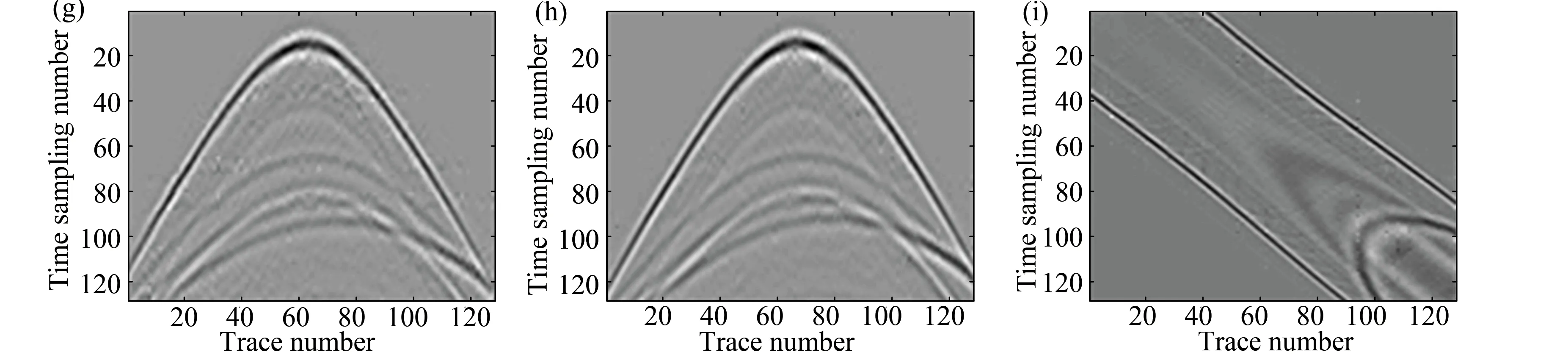

Fig. 7 Test on a synthetic 3D data. The center slices in three direction (t-x, t-y, x-y sections) of the 3D volume are displayed; (a-c) Original data; (d-f) Corrupted data with regularly missing traces; (g-i) Reconstructed data by the proposed method; (j-l) Difference between the reconstruction and original data
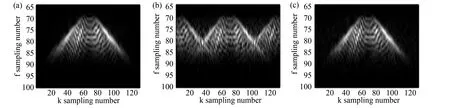
Fig. 8 (a)-(c) The f-k spectra of original data, corrupted data, and reconstruction as shown in Fig. 7(b), (e), and (h)
In this method, the random shift is an important parameter. How to design the random shift of each overlapped texture-patch and how to control the random overlapped texture-patch without zero rows are two common questions. In fact, it is not necessary to design the random shift of each overlapping patch. Instead solely randomly choosing a number will do, e.g., 1-5 columns for the shift. It does not need adaptive design. The method itself is a breakthrough that makes the low-rank patch methods work for regular downsampling. Previous low-rank patch methods only work for irregular downsampling.
The sensitivity of random overlapping to reconstruction SNR values and sensitivity of random overlapping to computational time were tested for the simulated 3D data, as shown in Fig. 9. Six random low patch-rank cases for each overlapping from 1 to 5 were tested, and then the six SNR values and computational time were averaged to obtain the final value for each overlapping. It seems the overlapping size can be taken as 3 to balance reconstruction SNR value and computational time.
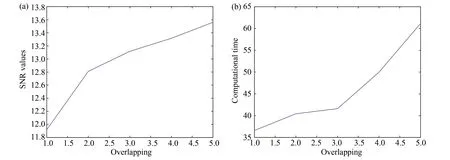
Fig.9 (a) SNR of reconstructed data v.s. overlapping; (b) Computational time v.s. overlapping
The shifts of overlap are random, so the size of matrix is different in each compute time. The random shift parameters need to be recorded and kept the same size when the matrix was transformed to the original domain. It is an easy operation, but a little bit additional memory is needed. It is also fine to use 0 to shift some patches. It is acceptable if it causes the matrix with zero row, because it is almost impossible to use 0 in all patches along the row direction. Randomness plays an important role here.
The performance of the proposed method on a real seismic data with a size of 256×256×16 is presented. A centralt-xsection is displayed in Fig.10 as an example. For the real data, the OR1MP shows competitive performance in terms of SNR value and computational time.
Fig.11 shows the close-up for a patch of the data. Fig.11(a) is the original data (left part) and the corrupted data (right part). Fig.11(b) and (c) are the LMaFit and OR1MP reconstruction (left part) and their error (right part). Because random-overlapped texture-patch mapping was used, the reconstruction results show a slight difference compared with the original data. To average them can further improve the result. For instance, the code was run four times for the real data while keeping the parameters unchanged. Averaging the four results, SNR=9.98 (a 62.89% improvement) and SNR=9.02 (a 29.04% improvement) can be obtained for LMaFit and OR1MP, respectively.

Fig.10 Test on real seismic data; (a) Original data; (b) Corrupted data with 50% missing traces; (c) Reconstruction by LMaFit (SNR=6.15, time=73.97 s); (d) Difference between the LMaFit reconstruction and the original data; (e) Reconstruction by R1OMP (SNR=6.99, time=46.96 s); (f) Difference between the OR1MP reconstruction and the original data
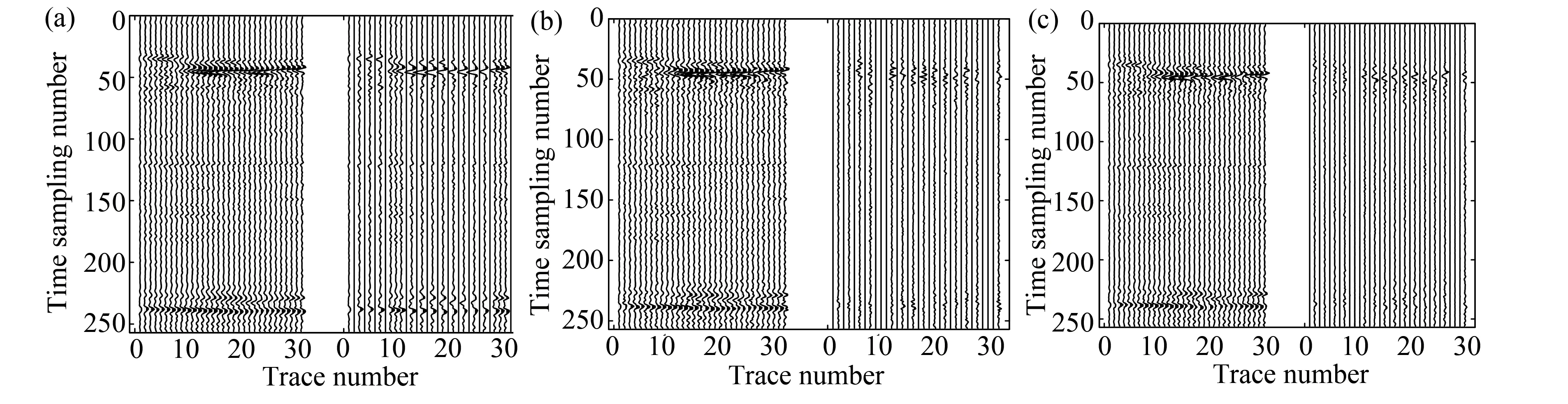
Fig. 11 The close-up of data; (a) Original data (left part) and corrupted data with missing traces (right part); (b) LMaFit reconstruction (left part) and its error (right part); (c) OR1MP reconstruction and its error
4 Conclusions and Future Work
A new low patch-rank method is proposed for the reconstruction of regularly missing traces in seismic data. Opposite to previous work where a regular texture-patch mapping based low-rank method was applied for randomly missing traces, random-overlapped mapping for regularly missing trace is considered in this paper. The basic assumption is that missing traces should increase the rank of the mapped matrix, or at least mapping should avoid zero or blank columns in the new mapped matrix, where the classic low-rank MC theory can be applied for reconstruction. The singular value plots show the performance of random-overlapped texture-patch mapping. Experiments show that the fast rank reduction algorithms, LMaFit and OR1MP, are efficient to solve the interpolation problem.
The low patch-rank method aligns all patches into a new matrix (mapping one patch from original matrix into one column in the new matrix), and then employs the NNM to reduce the rank. It works well for seismic data that have a globally similar texture pattern, but is not suitable for data that contain various different patterns. If the data does not have a globally similar texture pattern, one can add locally adaptive information into the model. A block method is the simplest model that enjoys globally dissimilar but locally similar seismic features. Other computationally expensive strategies such as shearing the patch data and defining a so-called block nuclear norm[47], and finding nonlocal similar cubes, can also be used to build a lower-rank matrix.
Frankly speaking, it is difficult for the current method to handle high missing-rate traces, especially for complex field data. One can incorporate it into other techniques to further improve the method. Application of the low patch-rank methods to 5D seismic data interpolation is straightforward. But the question of how to make use of the structures of high-dimensional data remains a problem for future research.
5 Acknowledgements
The author would like to thank Dr. Xinxin Li, Dr. Wenyi Tian, and Dr. Zheng Wang for their help and discussion in programming the code.
6 Appendix: OR1MP
The OR1MP algorithm to solve Eq. (12) includes two stages: pursuing the basis and then weighting the basis[38].
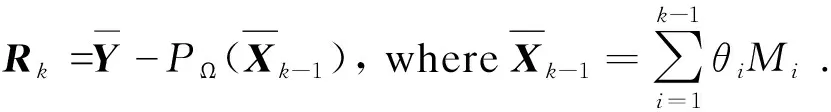
(13)
Furthermore,Mcan be written as the product of two unit vectors:M=uvT. Thus the above problem can be reformulated as
(14)
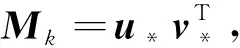
(15)
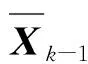
(16)
杂志排行
Journal of Harbin Institute of Technology(New Series)的其它文章
- γ-Fe2O3@carboxymethyl Cellulose as Potential Oral Nanomedicine for Iron Deficiency Anemia Treatment on Rats
- Evolution Toward Artificial Intelligence of Things Under 6G Ubiquitous-X
- Investigations about the Atomic Structure and Mechanical Behavior of Metallic Glasses after Melt Hydrogenation
- Review: Layer-Number Controllable Preparation of High-Quality Graphene for Wide Applications
- Review: Research Progress for Electric Vehicle Hub Motor Driving Technology
- Review:Chromatic Dispersion Manipulation Based on Optical Metasurfaces
