基于SOFM和BP短期负荷预测方法
2020-07-16朱雪凌
朱雪凌,程 然,王 为
(华北水利水电大学电力学院,河南 郑州 450045)
0 引 言
电力系统负荷预测是指以多种类型的电力负荷值、不同气象要素、金融、人文等历史参数,以及预测当天的天气预报信息为依据,对未来电力系统负荷值作出符合实际预测的完整过程[1]。
对电力系统日常运作管理而言,短期电力系统负荷预测是关键组成部分,准确地预测出期望的电力负荷,是电力系统运作计划制订的有力根据[2]。经过这些年国内外不少专家、学者的研究,一系列的短期负荷预测方法根据实际需求不断被改进创新组合,这些方法可以归纳总结为两大类:传统预测法以及现代预测方法[3]。传统的经典算法主要是根据数理统计的理论,建立出符合需求的时间序列模型,其中应用程度相对较高的有单耗法、时间序列法、回归分析法、弹性系数法等一系列数学模型;而人工智能技术的发展能够把现代人工智能方法、知识发现与机器学习都应用在负荷预测领域中,其中人工神经网络法以及专家系统法属于比较典型的理论,因此人工神经网络法作为本文研究的核心理论。
文献[4]使用Kolmogorov-Smirnov检验(K-S检验)对光伏发电出力历史数据作出分析,利用K-means算法将广义天气类型聚为3类。基于不同的聚类结果,通过人工神经网络算法分别建立了对应的光伏发电出力预测模型。文献[5]通过改进的模糊C均值聚类(FCM)算法,将数据日划分为晴天、多云、阴雨3类,针对每一类建立了光伏出力短期点预测和概率预测模型,并构建了基于遗传膜优化BP神经网络的组合预测模型和基于神经网络分位数回归和核密度估计的概率预测模型。文献[6]研究了一种基于模糊聚类和径向向量机的光伏发电预测法,实现了分布式光伏的功率预测,为功率控制提供前提条件。文献[7]提出了基于相似日聚类和利用共轭梯度法(CG)改进深度信念网络(DBN)的组合模型预测法。首先通过FCM聚类算法将原始数据按照隶属度做出相似日聚类,接着根据分类结果建立CGDBN预测模型,最后利用该模型对光伏输出功率作预测。
基于SOFM先聚类、神经网络再预测的模型以往多用在对疾病、天气方面的预测[8],近些年也逐渐开始有专家学者在负荷预测方面使用SOFM与其他神经网络相结合的预测模型,本研究因此提出一种以SOFM-BP神经网络为基础的预测方法,选取了2018年呼和浩特市的相关历史数据为研究对象,介绍了BP网络和SOFM网络的基本概念和原理,结合当地的实际情况,选取影响负荷的相应因素,最终构建出符合当地电力情况变化规律的组合预测模型。
1 BP的误差反向传播训练算法
1986年,以Rumelhart和McCelland为领导核心的科学实验小组在《Parallel Distributed Processing》一书中,详细阐述了BP网络为一种连续变换并具有非线性特征函数的多层感知器,BP的学习训练既含括信号正向传播阶段同时也存在反向传播误差的阶段[8]。由输入层接收初始信号并传入各隐层进行相应的计算变换,经传出层传出结果的过程即为正向传播。发现传出层真实传出值和预期设想值出入甚远的情况下,则开始将误差以相反顺序传播。反向传播即与原顺序方向相反,将期望和实际值产生的偏差从隐层传回至原输入层,根据逐层反馈产生的新偏差信息对各层神经元的连接权值逐一变化修改。通过如此反复交替信号正传与误差反传结合的学习训练方法,从而多次调整各神经元权值,该过程将持续至输出满足预期设想值,或训练至初始设定的最大次数而止。
本文选取了极为熟知的单隐层的BP网络,也即除输入层、传出层外只有一个隐层所组成的经典三层感知器。由图1可知输入向量为X=(x1,x2,…,xi,…,xn)T,隐层输出向量为Y=(y1,y2,…,yj,…,ym)T,输出层输出向量为O=(o1,o2,…,ok,…,ol)T,期望输出向量为d=(d1,d2,…,dk,…,dl)T。输入层与隐层所相连的权值,其所示矩阵为V=(V1,V2,…,Vj,…,Vm)T,列向量Vj在该矩阵中代表该隐层内第j个神经元连接两层的权值所对应的向量;隐层与传出层所相连的所有权值,其所示矩阵为W=(W1,W2,…,Wk,…,Wl)T,列向量Wk在该矩阵中代表该隐层内第k个神经元连接两层的权值所对应的向量。

图1 3层BP网
标准BP算法如下[8]:
(1)初始化。赋V、W任一数,偏差E初始为零,随机设置学习率η范围在(0,1]区间的某数,预置在某样本传入时输入计数值p和训练初始数目q均为1,并将精度Emin置为一符合期望的正小数。
(2)输入训练集,计算各层输出
(1)
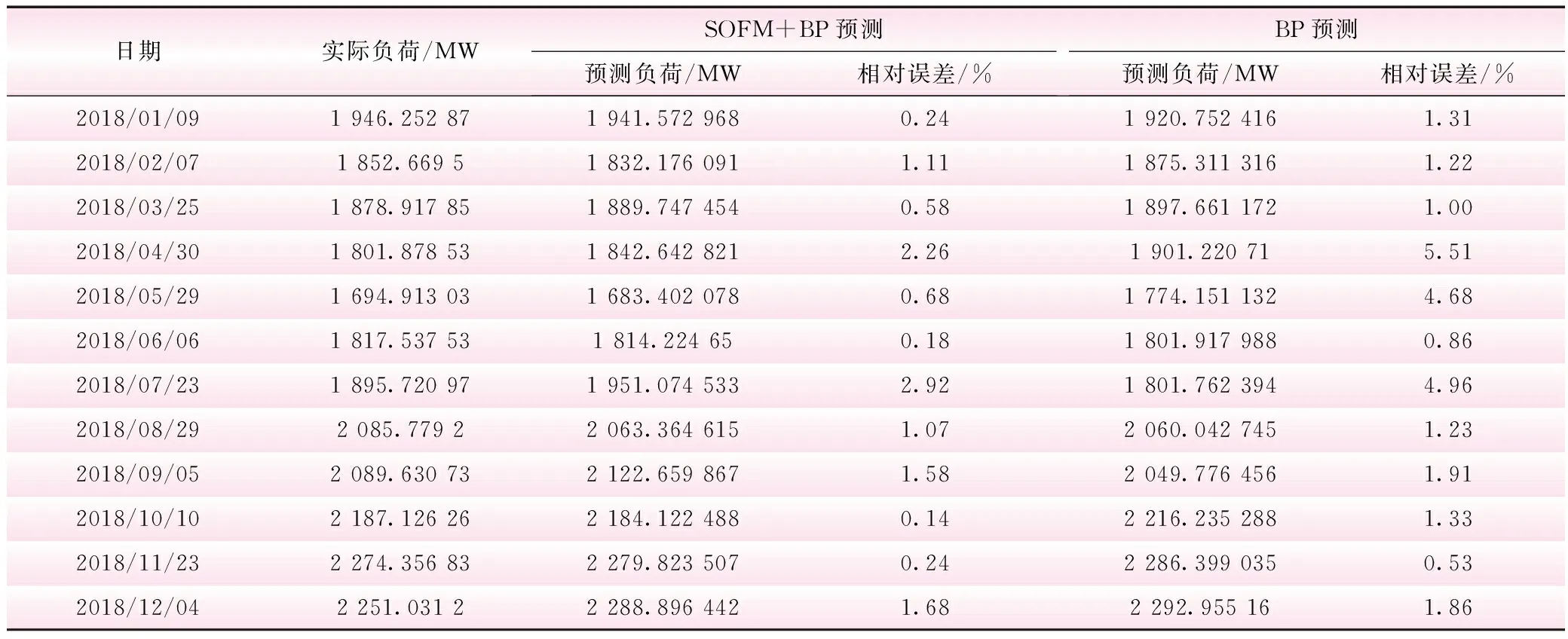
(6)查看训练集是否实现一次轮训。若p (7)检查网络总误差精度 。当ERME SOFM网络是由芬兰Helsink大学的T.Kohonen教授在1981年提出的,又称Kohonen网[9]。Kohonen提出设想:在受到外界某信号传入刺激时,该系统因被激励从而自动划分出多个领域,并因领域的差异而对输入模式产生特性迥异的响应,这一系列的过程是网络自主实现的。其仿效了人脑生物系统里的自组织特征映射性能,属于竞争型的自组织网络之一,在进入学习过程期间可以自主地开始无监督训练。 SOFM的基本结构通常有两层构成,即输入层和竞争层,在输入层里面所包含的全部神经元经由各个权值从外界把接收信号聚集至传出层内的一切神经元,神经元数量应保持在和样本维数等同。传出层既有传出信号的功能同时也具有竞争的功能,应用最多的布局格式多为一维线阵亦或二维平面组织,本文选用二维平面组织传出,在传出层内所有神经元在两侧方向直接相互连于其周边的神经元,该结构如图2所示。 图2 二维平面线阵 (4)确定优胜邻域Nj*(t)。确立t时以j*为中间位置的权值调节区域,大多数情况下最初设置邻域Nj*(0)范围相对较大,在以后的训练里Nj*(t)随时间推移逐步减少并缩紧其范围。 (5)修正权值。修正优胜邻域Nj*(t)中的全体权值 (2) 式中,η(t,N)为训练时刻t与拓扑距离N的函数变化关系,其中拓扑距离N为在邻域里竞争胜利的神经元j*与未胜利的第j个神经元两者的间距,该函数变化关系大多为:t↑→η↓,N↑→η↓,这种随时间增加而减小的函数也称之为退火函数。 (6)停止检查。以学习率η(t)逐步减至零或预设的某一数值为停止训练的标志,如不符合此条件则从步骤(2)重新执行。 以SOFM与误差反向传播算法相组合为基础模型的组合预测流程框图[10]如图3所示,学习过程中,首先应收集整理与负荷有关的多种影响因素资料和负荷历史数据用作训练集样本,并利用SOFM网络对所有处理过的训练集作聚类操作,根据分类后的不同子类建立、训练相应类别的BP子模型,最终经训练后的SOFM-BP组合模型即可实际运用在短期负荷预测方面。 图3 预测模型 采用该模型预测实际负荷时,应首先利用SOFM网对输入数据进行分类,根据分类的结果,激活对应的BP模型以预测负荷。 本文采用内蒙古自治区某市2018年历史日平均负荷数据作负荷预测,用本文的方法对该市一年的历史负荷数据建模分析,训练集为每月连续的20 d共240组数据,每组数据即SOFM输入层包括20个神经元,分别为预测当日、预测日前第一天和预测日前第七天的最高与最低温度数值、天气情况、风力大小、节假日类别、环境污染指数以及预测日前第一天和预测日前第七天的日平均负荷数值。由于短期负荷变化和气候有很大关联,在春夏季节,温度值越高,风力越弱,负荷越高;而转至秋冬季节时,则完全相反,即温度值越高,风力越弱,负荷呈现走低趋势。又因每个季节的气候对负荷产生影响的程度高低不一,本文通过不断实验,最终确定SOFM聚类将训练集分为4类最为合适。根据分类结果对每一类构建相应的BP模型,BP输入向量即预测日当天的最高温度、最低温度、天气、风力、节假日类别、环境污染指数以及预测日前一天和预测日前第七天的日平均负荷共8维,并对子类训练集进行相应训练。由于我们已经对原始数据进行了分类,所以在BP预测模型的输入中,不需要考虑预测日前一天以及预测日前第七天的气象因素,减少了BP预测输入数据过多带来的过拟合影响。 表1 SOFM-BP与BP预测日平均负荷结果 训练完成后,任取每月除训练集之外的10 d中任意两天共12 d作为测试集,利用该模型预测日平均负荷,所选测试集以囊括某种突出影响因素为优先选择,所以该12 d包括工作日、周末、节假日,包括优、良和有污染的环境指数,还包括各种不同风力和不同的晴雨天气,同时也加入了诸如高考特殊日。最终结果如表1所示,作为对比,表中还列出了直接使用BP网络预测的误差,其误差为预测值与实际值差值的绝对值比实际值。从表1可发现,采用SOFM-BP方法对日平均负荷作出预测产生的误差值最大为2.92%;而直接采用BP网络预测的最大误差为5.51%。在实验对比了二者的结果后发现,采用组合模型SOFM-BP方法的精度要高于仅用BP预测的理论方法。 本研究提出以SOFM的聚类特性和误差反向传播两种不同算法相组合为基本原理对短期负荷作出预测,改良了传统方法中负荷预测的部分缺点,缩减了训练时间,提升了预测精度。对未来日平均负荷的预测有一定的实际应用价值,也对电力调度有所帮助。2 基于SOFM的样本聚类
2.1 SOFM网络的结构
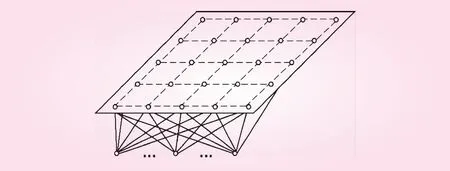
2.2 SOFM网络的Kohonen算法

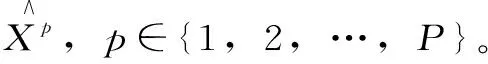
3 短期负荷预测模型

4 实例分析
5 结 语
