基于主成分分析的糯扎渡水电站弃渣场土壤流失量影响因素研究

李建兴，陈平平，陈胜利，刘 胜

(中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650051)

0 引 言

糯扎渡水电站建设伴随着大量移民工程，移民工程在施工过程中往往对原地貌造成剧烈扰动，并产生大量弃土弃渣。弃土弃渣结构松散，且在堆积的过程中形成较陡的坡面，自然坡度大都在25°～45°之间[1]，极不稳定，遇降雨易发生细沟侵蚀甚至坡面整体滑移。弄清弃渣场坡面水土流失特征，总结其水土流失规律，对正确评价开发建设项目水土流失影响，科学预测水土流失强度和水土流失量，合理布设水土保持措施具有重要意义。对于生产建设项目弃渣场水土流失规律研究，国外较少关注[3]。我国自20世纪90年代，大量的论文及著作探讨了生产建设项目水土流失的危害及成因[4- 6]，并在生产建设项目中提出了一些新理论、新技术和新方法。前人对水土流失预测及水土流失规律的研究主要集中在具体工程研究其水土流失规律，以及利用USEL应用于工程建设水土流失量的预测[7]。

糯扎渡水电站项目区降水在时空上的分布不均匀，暴雨频繁发生，再加上项目区土壤扰动面积较大，导致水土流失严重，研究该地区弃渣场土壤流失量及影响因素对防止土壤侵蚀、减少地表径流、增强坡面稳定性具有重要的理论意义。为此，本文通过研究弃渣场坡度、坡长及土壤孔隙对土壤流失量的影响，利用主成分分析法得出该地区土壤流失量及其影响因素的回归方程，为该地区弃渣场土壤流失量的预测及弃渣场生态恢复治理提供理论指导。

表1 弃渣场基本情况

1 材料与方法

1.1 试验区概况

糯扎渡水电站位于澜沧江下游普洱市思茅区和澜沧县交界处，为云南省澜沧江中下游河段水电开发方案的第5个梯级，电站装机容量5 850 MW，水库总库容237.03亿m3，正常蓄水位812 m，水库淹没区涉及到云南省普洱、临沧2个地区，9个县的48 475人，规划集中安置点60个。

为研究弃渣场土壤流失量的影响因素，在全面勘查糯扎渡水电站9个县60个安置点75个弃渣场的基础上，选取2015年度堆置完毕，未采取拦挡及植被恢复措施的22个弃渣场坡面作为研究对象。弃渣场基本情况见表1。弃渣场分布见图1。

图1 弃渣场分布

1.2 试验设计和样品采集

为研究弃渣场土壤流失量的影响因素，在每个弃渣场边坡内选取1块3 m×3 m的样方，在样方内将直径0.5 cm、长为30 cm的测针相距1 m×1 m分上、中、下垂直打入坡面，编号登记。另选取3块20 m×5 m的样地，利用侵蚀沟测量法测量样方内的侵蚀量作为基础数据。分别于2016年12月、2017年12月，记录坡面的坡度、坡向和周边情况，测量测针距离，并测量样方内侵蚀沟长、宽、深及形状，计算土壤侵蚀量，在每个样方内利用3个环刀(体积100 cm3)取土样，用于测定土壤孔隙度及土壤容重。

1.3 样品的测定和分析方法

土壤容重、毛管孔隙度、非毛管孔隙度、总孔隙度的测定采用环刀法[8]；弃渣场坡面坡度、坡长采用激光测距仪(LEICA DIDTO D5)测量。

降雨资料分别利用2016年～2017年度临沧市临翔区气象局圈内乡、马台乡、邦东乡的降雨观测值，景谷县气象局民乐镇、永平镇、碧安乡、益智乡的降雨观测值，澜沧县气象局谦六乡、糯扎渡镇的降雨观测值，以及思茅区气象局云仙乡、思茅港镇的降雨观测值。

采用Microsoft Office Excel 2010软件对测定数据进行处理分析及作图，用SPSS18.0软件对土壤侵蚀量与土壤理化性质及降雨、坡度、坡长进行Pearson 相关分析及主成分分析。

2 结果与分析

2.1 弃渣场坡度和坡长对土壤侵蚀量的影响

坡度是影响土壤侵蚀的重要因素。Zingg[9]研究发现，土壤流失量与坡度呈指数相关，公式表现为y=cxm。式中，y为单位面积土壤流失量；c为常数；x为坡度；m为坡度因子。Musgrave[10]研究发现，土壤流失量与坡度的1.35次方呈正比。Smith等[11]建立了土壤流失量与坡度的二次多项式关系。McCool等[12]建立了土壤流失量与坡度正弦值的线性关系，在缓坡条件下，效果较好。我国学者刘宝元等[13]分析陡坡情况下土壤流失量与坡度正弦值的线性关系。利用函数关系，得到坡度对土壤侵蚀量的影响，见图2。从图2可以看出，坡度在30°～42°范围内，土壤流失量与坡度呈现二次函数增加，公式表现为y=-260.42x2+21 550x-414 753(R2=0.708 7，P<0.05)，且显著正相关，研究结果与Smith的结果相似，说明随着弃渣场坡度的增加，土壤流失量逐渐增大，但存在最大值。

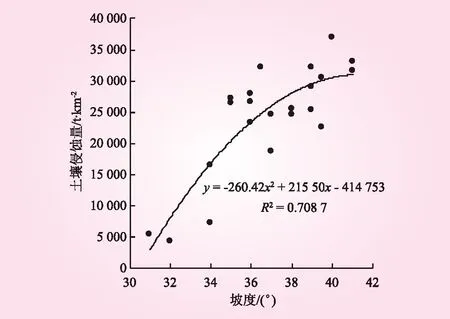
图2 坡度对土壤侵蚀量的影响

坡长是决定坡面能量沿程变化，影响坡面径流和水流产沙过程的重要地貌因素之一。前人研究[14]坡长与土壤流失量存在以下3种结论：①随着坡长增加，坡面径流含沙量增加，径流能力消耗于携带泥沙中，故土壤侵蚀反而减弱；②随着坡长增大，水深逐渐增大，土壤侵蚀量增大；③随着坡长增大，土壤侵蚀量从上坡至下坡无明显差异。本研究发现，随着坡长的增加，土壤侵蚀量与坡长呈对数函数关系(见图3)，公式表现为y=12 251lnx-19 020(R2=0.905 8，P<0.01)，说明随着坡长的增加，土壤侵蚀量逐渐增大，但坡长在0～60 m时，土壤流失量增加幅度较大，而坡长≥60 m后土壤流失了增加幅度缓慢，并逐渐趋于最大值。

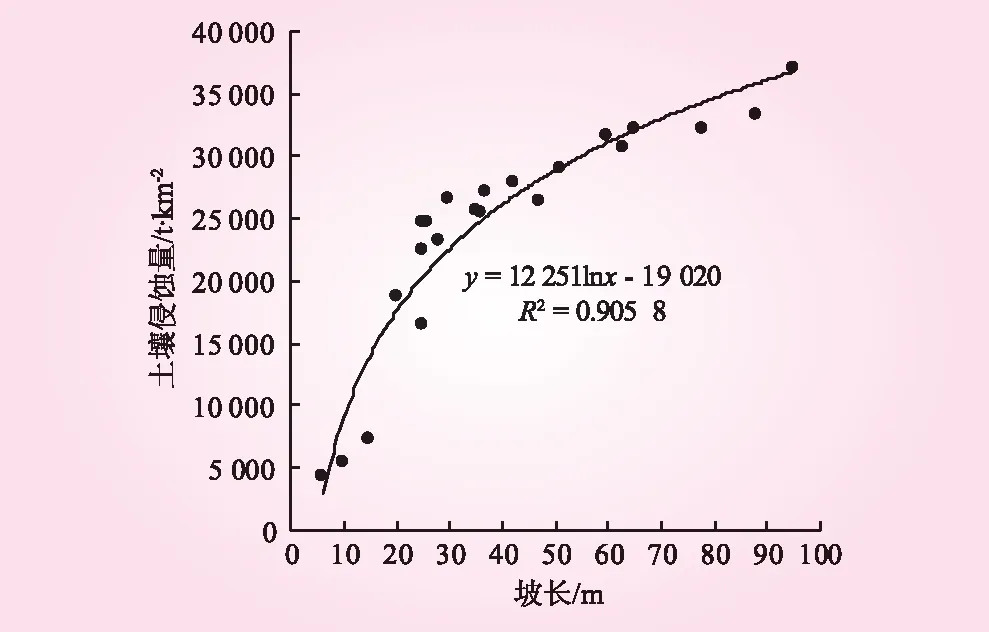
图3 坡长对土壤侵蚀量的影响

2.2 弃渣场土壤容重及孔隙对土壤侵蚀量的影响

土壤容重的大小直接反映了土壤孔隙的多少，容重小，孔隙多；土壤容重大，孔隙少[1]。利用函数关系，得到土壤容重对土壤侵蚀量的影响，见图4。从图4可以看出，土壤流失量随着土壤容重的增加呈线性增加，公式表现为y=95 664x-116 961(R2=0.825 7，P<0.05)，主要原因为土壤容重越大，土壤孔隙越小，渣场坡面入渗率越小，弃渣场坡面流能力越强，坡面产流时刻越早，径流系数越大，产沙量越大，导致土壤流失量越大[15]。

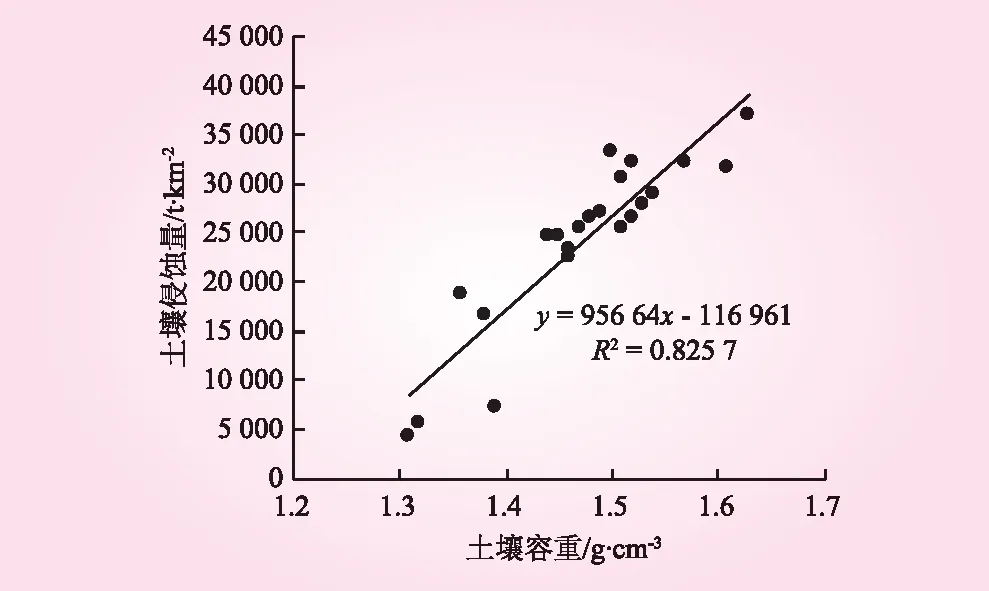
图4 土壤容重对土壤侵蚀量的影响

土壤总孔隙度及土壤非毛管孔隙度与土壤渗透性显著正相关[16]，土壤孔隙度大小直接影响地表土壤产流以及土壤入渗，而地表径流的大小决定了土壤侵蚀外营力的大小，从而影响土壤侵蚀量的大小。土壤总孔隙度对土壤侵蚀量的影响见图5。土壤非毛管孔隙对土壤侵蚀量的影响见图6。土壤毛管孔隙度对土壤侵蚀量的影响见图7。从图5～7可以看出，土壤侵蚀量随着土壤总孔隙度及土壤非毛管孔隙度的增加均呈现对数函数降低，公式分别表现为y=-85 578lnx+323 526(R2=0.808 2，P<0.05)，y=-47 046lnx+149 638(R2=0.808 2，P<0.05)，且显著相关；而土壤的毛管孔隙度呈不规律性。

图5 土壤总孔隙度对土壤侵蚀量的影响

图6 土壤非毛管孔隙对土壤侵蚀量的影响

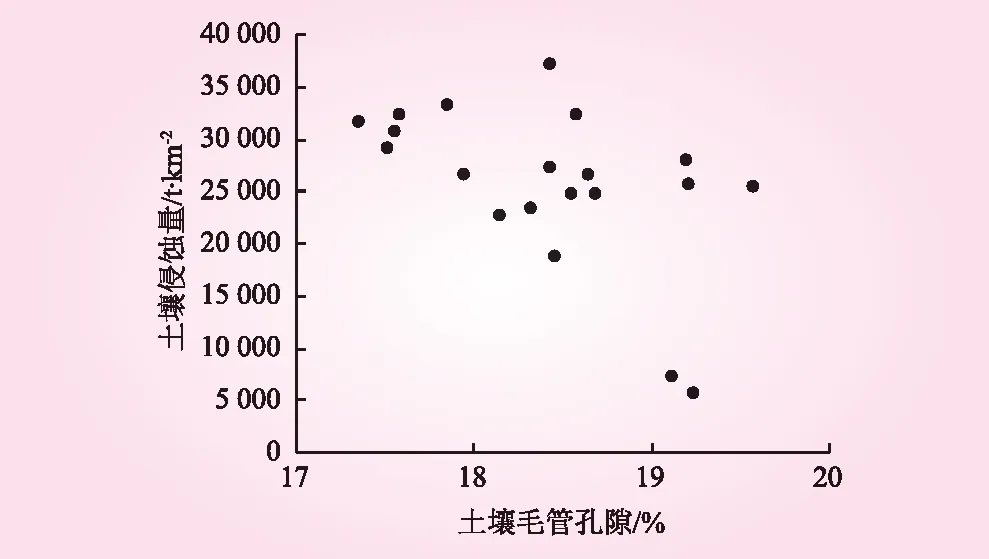
图7 土壤毛管孔隙对土壤侵蚀量的影响

2.3 土壤侵蚀量的影响因素

设弃渣场坡面坡度为β1，弃渣场坡面坡长为β2，各地区2016年度降雨量为β3，土壤容重为β4，土壤总孔隙度为β5，土壤非毛管孔隙度为β6，土壤毛管孔隙度为β7，土壤侵蚀量为α。利用SPSS进行相关分析，得出土壤流失量及其影响因素的相关关系矩阵，见表2。结果表明，土壤侵蚀量与弃渣场坡面坡度、土壤容重、弃渣场坡面坡长及年降雨量极显著正相关，而与土壤非毛管孔隙、总孔隙度极显著负相关，与毛管孔隙度显著负相关。

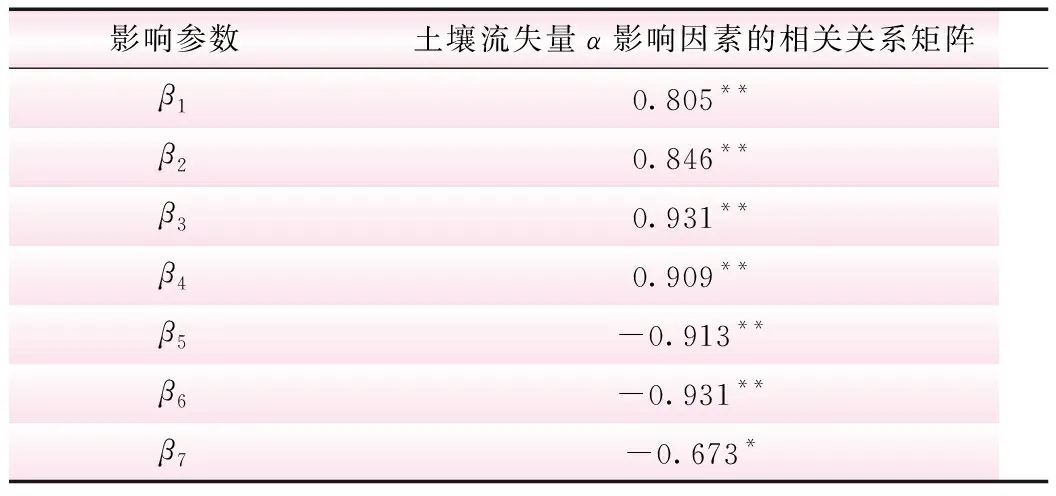
表2 土壤流失量及其影响因素的相关关系矩阵

注：*表示P<0.05；**表示P<0.01。

2.4 土壤侵蚀量影响因素的主成分分析

主成分分析是通过原始变量的少数几个线性组合来解释原始变量的绝大部分信息[17-18]。根据土壤流失量及影响因素的相关分析结果，选择与影响土壤流失量指标显著或极显著相关的因子，弃渣场坡面坡度β1、弃渣场坡面坡长β2、各地区2016年度降雨量β3、土壤容重β4、土壤总孔隙度β5、土壤非毛管孔隙度β6、土壤毛管孔隙度β7，对其进行主成分分析，结果见表3。从表3可知，土壤流失量的影响因子的第一主成分方差贡献率达81.945%，且各因子在第一主分量上的负荷量的绝对值均在0.718 5以上。其中，土壤非毛管孔隙β6的负荷量最大，为0.970；毛管孔隙度β7的负荷量最小，也高达0.819，表明与土壤流失量显著相关的因子的第一主分量表达了其绝大多数信息，表征影响土壤流失量各因子的综合参数β=-0.879β1′-0.865β2′+0.913β3′-0.906β4′+0.982β5′+0.970β6′+0.819β7。式中，βi′为各指标的标准化数据。

表3 土壤流失量影响因素主成分分析

以表征土壤流失量的综合参数α的标准化主分量得分为因变量，以流失量的影响因素特征综合参数β的标准化主分量得分为自变量进行回归分析，得到回归方程：α=0.909 6β-0.000 4，(R2=0.927 6，P<0.001)，达极显著水平。

3 结 论

本文基于主成分分析，对糯扎渡水电站弃渣场土壤流失量影响因素进行研究，得出以下结论：

(1)弃渣场坡面土壤流失量随着坡度及坡长的增加分别呈现二次函数及对数函数增长，公式分别表现为y=-260.42x2+21 550x-414 753(R2=0.7087，P<0.05)，y=12 251lnx-19 020，(R2=0.905 8，P<0.01)，均达显著正相关。

(2)弃渣场坡面土壤流失量随着土壤容重的增加呈线性增加，公式表现为y=95 664x-116 961(R2=0.825 7，P<0.05)；而与土壤总孔隙度及土壤非毛管孔隙度的增加均呈现对数函数降低，公式分别表现为y=-85 578lnx-323 526(R2=0.808 2，P<0.05)，y=-47 046lnx-149 638(R2=0.808 2，P<0.05)，且显著相关；而与土壤的毛管孔隙度呈不规律性。

(3)土壤流失量与弃渣场坡面坡度、土壤容重、弃渣场坡面坡长及年降雨量极显著正相关，而与土壤非毛管孔隙、总孔隙度极显著负相关，与毛管孔隙度显著负相关。

(4)经主成分分析，得到表征影响土壤流失量各因子的综合参数β=-0.879β1′-0.865β2′+0.913β3′-0.906β4′+0.982β5′+0.970β6′+0.819β7，并构建了土壤流失量α与影响土壤流失量各因子β的回归模型α=0.909 6β-0.000 4，(R2=0.927 6，P<0.001)，该模型有无普适性有待进一步验证和校正。

需要说明的是，前人研究发现[5- 8]，弃渣场土壤流失不仅与以上因子有关，还与土壤次降雨因子、土壤本身可蚀性、土壤机械组成、有机质含量等因素有关，而这些因子对本模型的影响如何，有待进一步研究。