基于局部敏感哈希的改进堆叠算法

王俊杰，温雪岩*，徐克生，于 鸣

(1.东北林业大学 信息与计算机工程学院，黑龙江 哈尔滨 150040；2.国家林业局哈尔滨林业机械研究所, 黑龙江 哈尔滨 150086)

堆叠泛化(stacking)是机器学习领域中一种突出和流行的元学习方法，适用于计算机视觉和计算生物学等领域的各种机器学习任务[1]。Stacking与Bagging、Boosting等算法类似，是一种采用异质集成策略的集成学习方法，其在更高假设空间具有更好的表达能力，并且可获得比单学习器更好的学习效果。随着Stacking方法在解决数据挖掘、文本分类、信息安全和图像处理[2-5]等方面问题的日益普及，它也在诸如kaggle、天池等之类的各大竞赛平台中成为一种不可缺少的关键技术。

Wolpert[6]提出的堆叠算法巧妙地使用了交叉验证来生成高层数据，再通过训练高层数据进而得到结果。Ting等[7]将交叉验证替换成了Bagging和Disjoint方法来生成高阶数据以求得更精准的结果，并且发现Bagging方法对不稳定算法和稳定算法都有效，但尚未对存在的几种堆叠方式的时间复杂度做对比，以及对算法稳定性作出有效证明；Sill等[8]提出了一种线性技术，即特征加权线性叠加(FWLS)，它使用元特征(描述数据集中每个示例的附加输入)可以提高集成方法的性能，其最大收益来自需要大量调整和训练时间的非线性过程；吴挡平等[9]针对Bagging、Adaboost算法对稳定性分类算法集成效果不好的问题，提出基于Stacking的稳定分类器组合算法，以得到更高分类准确率的效果；Arsov等[10]分析了Stacking、bag-stacking(BAG)和dag-stacking(DAG)的假设稳定性，并建立了堆袋和加重堆袋之间的联系，最后证明了叠加的假设稳定性是每个基本模型和合并器的假设稳定性的乘积。

然而，目前对堆叠的工作原理、方式等技术领域的研究相对较少，仅有少量研究人员发表了罕见的博客或文章，其中的解释往往基于直觉，没有更具说服力的理论支撑，缺乏理论洞察力。堆叠泛化作为交叉验证的“复杂版本”,有着与生俱来的高复杂性以及“数据泄露”问题。堆叠泛化的高时间复杂度来源于交叉验证，它将分组后的数据交替进行训练与测试，与其他机器学习算法相比，其复杂性不言而喻。堆叠算法在适应模型特征时，使用了本不可见的测试集信息，出现了数据泄露的问题。分析学习算法泛化能力的一种常见方法是看它对训练集中的小变化的敏感程度，用不同的稳定性概念来量化，就可以在稳定性和泛化之间建立精确的关系，借此关系可以消除一定的堆叠算法的不稳定性。

本文针对上述堆叠的研究少有体现在时间复杂度、“数据泄露”以及算法稳定性方面的问题，提出一种介于BAG和DAG方法之间的基于LSH的Stacking算法，这里简称为LBDS(LSH-BAG-DAG-stacking)。LBDS摒弃了繁琐复杂的k折交叉验证，而是利用LSH算法获得“主流”数据并通过其完成整体的训练。LBDS首先将训练集和测试集映射到哈希桶，当其中某个桶满时作为开始训练条件，训练出的模型对下一次桶满时的训练数据和测试数据及其邻域进行预测。接着利用稳定性和信息熵条件对基分类器筛选，生成高层数据，最后将高层训练预测得到的结果通过混合投票和平均的方法求得最终分类结果。

1 理论分析与设想

Stacking的设计之初就伴随着很高的时间复杂度，并且存在着一定的“数据泄露”，这些问题限制了Stacking的发展，本章主要从这2个方面出发并附加算法稳定性进行问题阐述。

1.1 Stacking

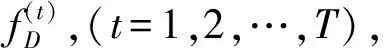
(1)

(2)

简化为

(3)

式中g为组合器的模型方程。其中常见的2种不同的Stacking如图1所示。

图1 2种不同的Stacking构造算法

传统的Stacking算法采用k折交叉验证来生成元数据，但交叉验证具有高复杂性，同时也存在着“数据泄露”的现象。交替训练和验证k折数据，其时间复杂度变为原来的k倍。将模型S拟合到数据d0，对数据d1进行预测并评估性能。但是d0中的元函数取决于d1中的标签值。因此，这种泄漏就是我们试图预测的目标值本身就已嵌入到我们用来适应模型的特性中。理论上S可以从元特征中推断出有关标签值的信息，从而使其过度拟合训练数据，而不能很好地预测测试样本。实际上，研究人员很容易忽略这个理论上的漏洞。文献[7]中选择用Bootstrap或Disjoint采样代替交叉验证，假设有N′个样本的随机样本，L Boostrap可表示为当N≤N′时，随机样本L替换为大小为N的k个子集合，Disjoint则可表示为当N≤N′时，随机样本L替换为k个大小为N的不相交子集，Bootstrap和Disjoint差别在于子集是否存在局部重复性。

1.2 局部敏感哈希

以往算法采用欧氏方法计算样本之间距离极为耗时[11]，LBDS采用 LSH[12-13](局部敏感哈希)的方式来保证训练数据差异性和查找待测样本的近邻。LSH 是一种高维空间最近邻搜索算法，其基本思想是：通过选取的哈希函数的映射变换能够将原始的数据集划分为若干较小的子集，且每个子集中的元素个数较小且相邻。其形式化定义如下：

定义1(局部敏感哈希函数簇) 对于Hash函数簇H中每个函数h，如果任意2点p、q满足以下条件，则认为H是(ddist1,ddist2,P1,P2)敏感的：

1)若d(p,q)≤ddist1,则

PH[h(p)=h(q)]≥P1;

(4)

2)若d(p,q)≥ddist2，则

PH[h(p)=h(q)]≥P2。

(5)

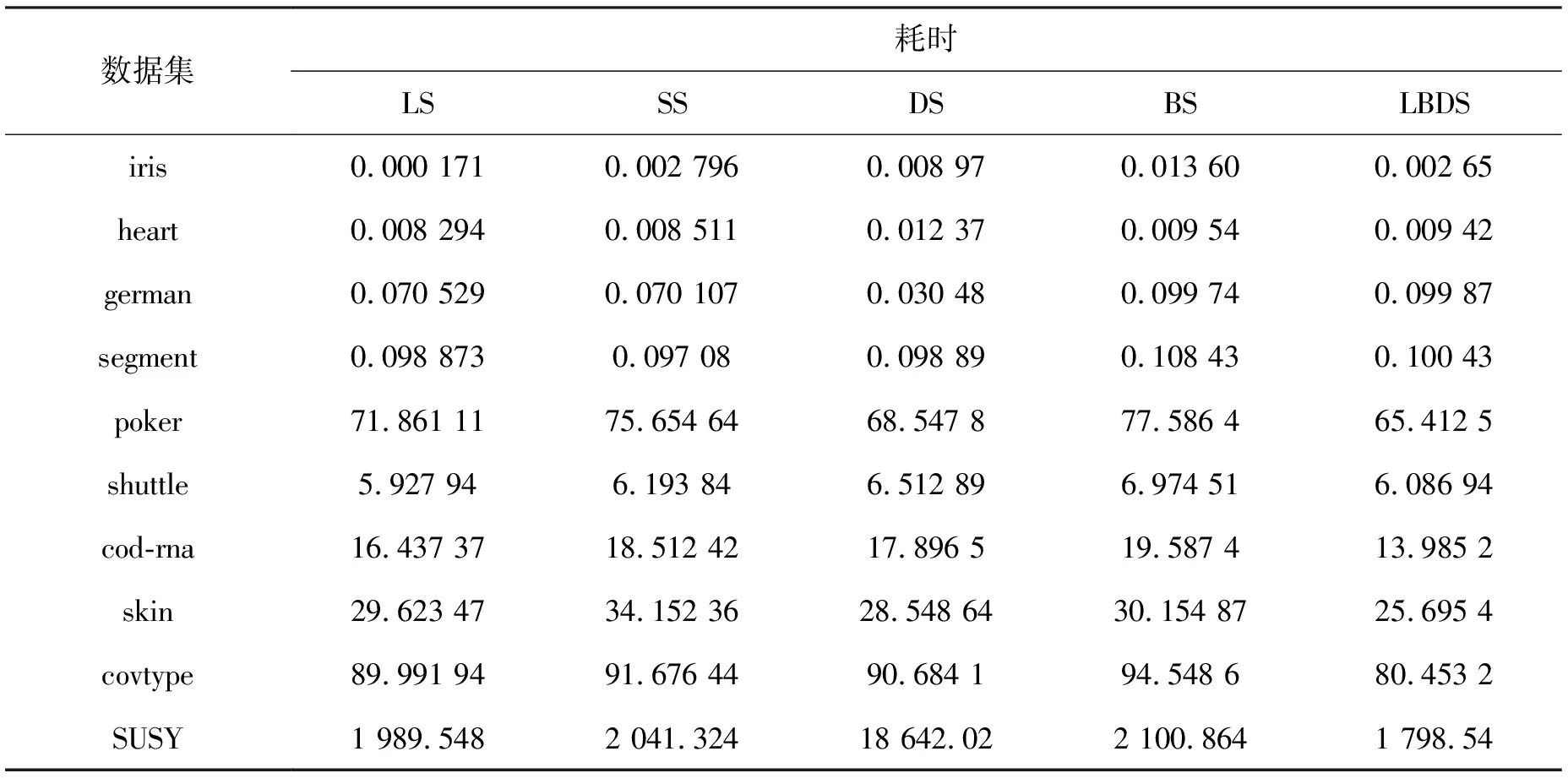
式中：ddist1

局部敏感哈希常用的距离度量有汉明距离、欧氏距离和余弦距离，对于LBDS处理数据向量则选取余弦距离来表示最为合适，对于存在于k维的2个点m和n(m、n为向量)，两者的相似性为

(6)

式(6)表示向量m、n之间的夹角余弦值，值越大，则m、n越相似。

以二分类(A、B两类)数据为例，用包含3个哈希桶的LSH对2类数据进行处理。假设A类数据经哈希映射落入桶1、桶2中，该类数据相对于B类数据多且分布广，所以桶1和桶2中的A类数据更新非常快，这样可以快速适应数据动态的变化，桶3则完整保留B类数据，如图2所示。同理，多分类亦然。

图2 LSH数据保存梗概

在算法训练之初建立一张空的哈希表，针对获得的数据，将数据分别映射到表中多个固定容量的哈希桶中，若一个桶中的数据超过其容量，则对所有桶进行训练，并将满桶置空，用新数据继续填充该空桶。对于当前桶满轮次获得的模型，将对下一个桶满轮次映射到哈希桶的训练集和测试集的邻域进行预测，通过对多个数据块的处理，建立一张保存了数据分布梗概的哈希表。从直观上说，放弃交叉验证能避免一定的“数据泄露”现象。LBDS算法(基模型m对第一次桶满数据预测)如图3。

图3 LBDS算法

1.3 算法稳定性

数据的采样策略可能导致高偏差与高方差，造成模型不稳定。文献[14]利用叠加过程中各组成模型间假设稳定性的相互作用分析相对于z=(x,y)的预期绝对损失误差。

定义2(随机假设稳定性) 假设训练集D={zi=(xi,yi),i=1,…,m}∈Zm从属于分布P中提取的，给出一个算法A，A(D)表示算法A对数据集D训练的模型，这里令A(D)=fD，l为损失函数，Ez表示z的期望，Di表示D{zi}，即数据集D移除了点zi=(xi,yi)。如果以下条件成立，随机算法A具有随机假设稳定性βm，即

ED,z[|l(fD,z)-l(fDi,z)|]≤βm,∀i∈{1,…,m}。

(7)

文献[10]为了分析叠加的假设稳定性，有以下2个假设：1)基学习算法彼此独立；2)元学习算法独立于基学习算法。因此，每个基算法的稳定性独立于其他算法，合并器算法的稳定性也独立于基算法的稳定性[15-16]。上述稳定性的叠加性是基于基分类器和元分类器的相互独立的假设，在实际中，并不能保证分类器之间具有完全的独立性。可以利用差异性来衡量分类器之间的独立性，计算个体分类器间差异度的方式有：K度量[17]、难度度量θ[18]、广义多样性GD[19]、熵度量E[20]等。文献[21]提出一种利用多个分类器的分类结果的熵值来表征分类器间的差异程度的熵度量，它没有使用对数函数，更易处理且能快速运算，其计算公式为

(8)

式中：N代表样本数；L代表基分类器数目；zj表示第j个样例；l(zj)表示对样例分类正确的分类器的数量。如果所有的基分类器对于样例zj输出结果一致，即没有差异，则此时熵度量值为0；如果仅仅有[L/2]的分类器分类正确，则熵度量值为1，此时集成系统的差异性最大。

2 算法设计与实现

训练阶段，当下一轮次桶满的时候，我们用本轮次的模型对训练集进行预测，得到相应的分类准确度，利用式(8)得分类器群差异度最大，并且分类准确率较高的Num个分类器，筛选出对应的训练集元特征，最后用Num个分类器对测试集进行预测，得到测试集元特征。

算法预测阶段，针对每一个样本的n+1个预测结果，使用混合投票和平均的方法来确定最终结果，经过大量实验，决策公式定义为

(9)

2.1 算法描述与流程

输入：训练数据DT，样本类标签数量n，k种基分类算法{A1,A2,…,Ak}，桶满次数m，元分类器B，测试样本DS，哈希桶数量C以及容量S。

(Ⅰ)生成level 1训练集：

1)创建一张包含了C个桶且每个桶容量为S的空哈希表HT；

(Ⅱ)生成level 1测试集：

(Ⅲ)元学习器对level 1层数据进行训练测试：

算法流程如图4。

图4 算法流程

2.2 算法分析

LBDS从数据采样策略以及算法稳定性2个方面对Stacking进行优化，其中的LSH方法采样对时间复杂度和“数据泄露”有一定的降低和缓和。

2.2.1 LBDS时间复杂度

设x和y分别为训练数据和测试数据大小，有m种基分类算法(假设筛选了1/2)，n为类别数量，s为桶的数量，那么对于LBDS来说，数据映射到哈希表所需时间为O(x+y)。考虑到极端情况，假设每一次满桶都是由一个仅差一个数据的桶所致(每个桶数据均分)，每次数据用m种分类算法训练分类器所需时间最长为O(mxs)，最少为O(mx), 那么生成level 1训练集数据所用时间最长为O(msx), 最短为O(mx)；生成level 1测试集数据所用时间是固定的O(my(n+1)/2)。在level 1层训练和测试的复杂度与生成时相同，则其花费的时间复杂度最长为O(m(2sx+y(n+1)+x+y)),最少为当n=1时，也就是二分类时，O(2m(x+y)+x+y)。由此可见，桶容量的设置(即桶的设置个数)和类别数量以及测试数据的选定对本算法十分关键。假设数据服从高斯分布，那么桶满速度较快表示数据更迭快，其所代表的数据就是随机变量取值的集中趋势点，即LBDS时间复杂度与集中趋势点有正相关联系。

2.2.2 数据生成

LBDS使用LSH算法将数据映射到哈希桶里，在某个桶满之后利用k个算法进行训练，训练结束后将桶清空。这样做的目的是代替交叉验证，从理论上说训练结束是以训练数据中样本数量最多的类别结束为终止条件，其存在的重复情况大大减少。最后利用LSH算法得到待测样本的近邻样本，将对新的近邻样本的预测与交叉验证中对测试集的预测进行合并，这从某种程度上缓和了“数据泄露”的情况。

2.2.3 LBDS的稳定性

对于LBDS，根据式(2)以及2个假设有以下证明。假设在每次桶满去除训练的数据为i，这里写成Di，表示D{i}，即数据集D移除了某个桶i，则有：

1)对于每对基础模型的结果βs和βt，有：

(10)

(11)

从而有

(12)

(13)

结合式(10)、(11)有

(14)

由式(14)可以看出，叠加的假设稳定性是所有基本模型和合并器假设稳定性的乘积。基础算法和合并算法之间的独立性使计算变得容易。另外，增加基础模型的数量可以提高堆叠的稳定性。

3 实验结果与分析

本次实验在具有6个Intel Xeon Silver 4116@2.10 GHz CPU的计算机上实现，操作系统为CentOS, Python版本为3.5.2。本次实验主要从3个问题出发进行验证：1)与现有的方法(如基于类标签和概率的Stacking、bag-stacking和dag-stacking)相比，LBDS的性能;2)时间复杂度，即训练模型所花费时间；3)算法的稳定性。

在实验中采用了经典的支持向量机(support vector machine，SVM)、贝叶斯(navie Bayes)、决策树(decision tree)、BP神经网络(backpropagation neural network),K近邻算法(KNN)、逻辑回归算法。其中SVM使用的核是Gaussian，决策树中采用CART决策树，贝叶斯方法中采用Gaussian，将逻辑回归作为元分类器，其余作为基分类器，并设置4种方案作为对比：LS——标签分类(label stacking)为基础的Stacking算法,如图1(a)所示；SS——分类器预测分数(score stacking)为基础的Stacking算法,如图1(b)所示；BS——bag-stacking算法，即其数据采样采用Boostrap方法；DS——dag-stacking算法，即其数据采样采用Disjoint方法。

为了验证算法设想，从UCI和Statlog 这2个公开数据集中选取具有数量级梯度的数据集，数据集汇总见表1。

表1 公开数据集一览

在本实验中，LBDS的桶数量设置成样本数量最多的类别的1/4，除LBDS外其他算法一律使用5折交叉验证。算法对数据集的训练和验证性能表现选用准确率(Acc)和ROC曲线下与坐标轴围成的面积(AUC值)作为评价标准，在选取训练集和测试集的时候，引入了随机性，为此，进行了多次实验(5次实验)，并记录各个算法在各数据集上表现情况(平均Acc和AUC值，结果保留3位小数)，结果见表2(其中多分类的AUC为宏平均和微平均，如0.98/0.98)

表2 数据集上各算法的Acc和AUC对比

通过5次实验，统计出各算法在各个数据集上的表现情况见表3。由表3的数据可以看出，LBDS算法与其他算法相比有着更好的性能表现。LBDS、BS、DS与LS和SS公共的不同就是采取了非交叉验证的策略。交叉验证有着一定的“暴力美学”，它检验所有的数据集，理论上会产生更优的结果，但“数据泄露”问题容易使交叉验证出现过拟合，在测试集上的泛化能力会适得其反。而bag-stacking、dag-stacking有着不同的数据采样策略，bag-stacking重复随机采样在大概率上获得数据的整体结构，操作简单，但采样的次数和数量对结果的影响很大；dag-stacking对不重复的子集进行训练，其优点是速度较快，但很有可能不能完全掌握数据的整体结构。

表3 算法在数据集上预测平均准确率

通过表2可以看出，DS和BS的Acc和AUC值比LS和SS更佳，DS和BS平均表现在6个数据集上优于LS和SS，平均性能高了2%。而LBDS在8个数据集上优于其他算法，表现在数量级较高的数据集上，表明LBDS对高维数量级有着一定的优越性。分析表3可以得到LBDS在小样本数据集上表现较差，而在大样本数据集上一直表现良好，可见其在较大数据集上具有良好的分类效果。经过多次训练可看出LBDS表现出的优越稳定性，这在解决大数据问题上有很大的潜力。经LBDS算法的部分数据集ROC曲线如图5。

图5 LBDS在部分数据集上的ROC曲线和AUC值

衡量算法的性能还需考虑算法的时间复杂度，本文对算法训练和测试的平均时间进行统计，其结果见表4。

由表4可以看出堆叠算法的高时间复杂性，其本身策略就是牺牲时间复杂性来换取更好的分类性能。LBDS在低数量级上的时间复杂度接近于甚至高于其他算法，而在高维数据上有着平均约10%的时间节省，可见LBDS的样本采取策略在大数据上有着一定的优越性。

表4 算法平均时间复杂度统计

综上所述，本文提出的LBDS算法在处理大量数据时有着明显的优势。在10个实验数据集上显示：LBDS算法Acc和AUC值通常高于常用的4 种堆叠算法而且性能更加稳定，说明本文提出的LBDS 算法是有效可取的。

4 结语

针对Stacking方法在数据挖掘、图像处理、自然语言处理等机器学习领域上的应用越来越广泛，而时间复杂度和分类效果是其最重要的2个技术指标。本文提出一种基于LSH的Stacking方法(LBDS)，首先利用LSH算法生成0层数据，再利用稳定性和信息熵条件对基分类器筛选，生成高层数据，最后通过投票法和平均法得到最终分类结果。通过在UCI和Statlog公开数据集上筛选的数据集验证表明，LBDS确实对Stacking方法本身存在的高复杂性、“数据泄露”问题进行了一定的改进以及对算法稳定性进行了加强，这对于Stacking在相关应用领域内的时间复杂度以及稳定性方面具有一定的实践价值。另外，LBDS对图像和自然语言等问题的大数据处理的高复杂性问题的研究提供了一定的理论指导意义，同时也为聚类、回归等问题的稳定性研究提供了理论参考。