中药复方汤剂煎煮质量评价数学模型研究*
2020-07-15陈树和闫斌陈洪燕陈闻捷孙婉瑾周从辉朱田密黄正德陈蕾李学林刘瑞新
陈树和,闫斌,陈洪燕,陈闻捷,孙婉瑾,周从辉,朱田密,黄正德,陈蕾,李学林,刘瑞新
(1.湖北省中医院药事部,武汉 430061;2.湖北省中医药研究院中药研究所,武汉 430074;3.河南中医药大学第一附属医院药学部,郑州 450000)
汤剂,古称“汤液”,是我国最古老、最常用的中药传统制剂,具有服用方便、吸收快、载药量大、疗效显著等优点,其临床疗效与饮片质量、煎煮方法、煎煮质量控制、服用方法等多种因素有关[1-2]。随着人工智能大数据平台在医药领域中的广泛应用[3],以患者在中药饮片代煎取药的过程为例,在处方调剂、饮片拍照存档、计算加水量、控制煎煮时间、实时告知患者煎药进度等步骤,均有人工智能大数据平台在应用。然而,中药汤剂质量检查项目与质量标准的制定一直处于空白状态,导致中药汤剂煎煮质量评价的可操作性标准难以落实。因此,以常用中药饮片煎煮的参数为基础,开发监测和评价中药汤剂煎煮质量的人工智能大数据平台,对确保中药汤剂煎煮的质量和临床疗效具有重要意义。
在“十三五”国家重点研发计划项目“中药饮片智能调剂与煎煮设备关键技术研究”的立项资助下,本课题组完成了197种常用中药饮片煎煮吸水率、相对密度、出膏率等煎煮参数的测定,并依据药用部位进行分类分析,分为果实种子类、根及根茎类、花叶全草类等,分别以该药用部位中药煎煮的相对密度与出膏率的数据建立了预测本药用部位多种中药煎煮的相对密度95%预测区间的数学模型,并经过实验验证,结果均在该药用部位相对密度95%预测区间数学模型的预测范围之内。在此基础上,本研究以197种单味中药饮片煎煮的参数建立中药复方汤剂煎煮相对密度95%预测区间数学模型,并以麻杏石甘汤为例,单独建立麻杏石甘汤煎煮相对密度95%预测区间的数学模型,以麻杏石甘汤进行煎煮实验验证这两种数学模型,以期为中药复方汤剂煎煮的质量控制研究提供参考。
1 仪器与试药
1.1仪器 AU-120L型高精度密度测定仪(密度解析=0.0001 g·cm-3),杭州金迈仪器有限公司;DHG-9146A型鼓风干燥箱,上海习仁科学仪器有限公司;ME204E型万分之一电子天平(感量:0.1 mg),瑞士梅特勒-托利多公司;ZNHW智能恒温电热套,天津工兴实验室仪器有限公司。
1.2试药 197种中药饮片分别购自安徽人民中药饮片有限公司、安徽普仁中药饮片有限公司和亳州沪谯中药饮片有限公司,每种饮片3批,饮片质量均符合2015年版《中华人民共和国药典》标准或2005年版《安徽省中药饮片炮制规范》标准。所有批次的中药饮片经湖北省中医院药事部陈树和主任药师鉴定为正品。实验用水为自来水。
2 方法与结果
2.1单味中药饮片煎煮吸水率、得液量、相对密度、出膏率的测定
2.1.1吸水率 选取临床常用的197种中药饮片进行煎煮实验,依据药用部位分为根及根茎类、果实类、种子类、花类、叶类、全草类、动物类、矿物类、皮类、茎木类、其他类等11种,见表1。每种饮片称取50 g置于1 000 mL圆底烧瓶,置于智能恒温电热套中回流煎煮。依据中药饮片药用部位及质地差异,一煎加水量为饮片质量7~12倍,二煎加水量为饮片质量6~10倍,浸泡30 min后,一般饮片一煎30 min,二煎20 min;滋补类饮片一煎60 min,二煎40 min;后下饮片如豆蔻、砂仁等一煎5 min,二煎20 min;其他后下饮片一煎10 min,二煎20 min;矿石、贝壳、角甲类中药饮片先煎煮30 min,毒性中药饮片先煎煮60 min,再一煎60 min,二煎40 min[4-7]。滤过后测定滤液体积,分别计算一煎吸水率、二煎吸水率。饮片吸水率公式:煎煮吸水率(%)=(加水量-滤液体积)/饮片重量×100%(公式1)。
2.1.2煎煮得液量、相对密度、出膏率 以“2.1.1”项测定单味中药饮片煎煮吸水率为基础,再次进行煎煮实验,测定药液得液量(mL)、相对密度、出膏率(%)等参数。
以中药汤剂每日服用剂量500 mL(分两次服用,每次250 mL)进行计算,要求一煎得液量和二煎得液量均为250 mL,饮片加水量公式:一煎(或二煎)加水量=一煎(或二煎)吸水率×饮片重量+250 mL(公式2),合并两次煎煮的药液,在(80±1) ℃测得液量和药液相对密度,并在(80±1) ℃精密量取药液25 mL,置已干燥至恒重的蒸发皿中,水浴蒸干,烘箱中105 ℃再干燥3 h,随后移至干燥器中,室温放置30 min后迅速精密称定,计算出膏率。饮片出膏率公式:出膏率(%)=干膏重/饮片重量×100%(公式3)。

197种单味中药饮片煎煮测定的一煎吸水率、二煎吸水率依据不同药用部位饮片吸水率的平均值进行分析,结果见图1。出膏率结果依据不同药用部位饮片出膏率的平均值进行分析,其中茎木类、矿物类、动物类中药饮片出膏率的平均值<10%,其他8种药用部位中药饮片出膏率平均值>10%,见图2。以不同药用部位饮片出膏率进行单因素方差分析(在SPSS 20.0版统计软件中采用未假定方差齐性的Tamhane’s T2进行两两比较),在α=0.05水平下,茎木类、矿物类、动物类中药饮片的出膏率,与除了其他类中药饮片以外的7种药用部位中药饮片的出膏率均差异有统计学意义,结果见表2。

表1 197种中药饮片品种明细

图1 不同药用部位中药饮片吸水率平均值结果
Fig.1 Results of average water absorption rate of TCM decoction pieces in different medicinal parts
2.2以197种单味中药饮片煎煮的参数建立相对密度预测区间的数学模型1
2.2.1建立单味中药饮片煎煮校正的相对密度对出膏率的线性回归方程 按最小二乘法,以197种单味中药饮片煎煮的相对密度(Y,为经过公式4的校正值)对出膏率(X,%)进行回归,得回归方程为:Y=0.000 4X+0.996 4(方程1),相关系数r=0.977 0,线性范围为0.2%~90.4%。

图2 不同药用部位中药饮片出膏率平均值结果
Fig.2 Results of average paste-forming rate of TCM decoction pieces in different medicinal parts
2.2.2回归方程的假设检验 为了检验方程1是否对总体线性回归方程存在回归系数β≠0的可能,需要对线性回归方程进行假设检验,采用SPSS 20版软件(IBM SPSS statistics 20)对校正的相对密度进行方差分析,得F=1 435.270,查临界值表F0.05/1, 195=3.890,故P<0.01,按α=0.05水准,接受回归系数β≠0,认为校正的相对密度与出膏率之间有线性关系,线性关系显著,总体线性回归方程成立。
2.2.3建立数学模型 结合方程1单味中药饮片煎煮相对密度对出膏率的线性回归方程,推测该方程也适用于中药复方汤剂煎煮相对密度对出膏率的关系,即中药复方汤剂煎煮的相对密度为:Y复方=0.000 4X复方+0.996 4(方程2),Y复方为中药复方汤剂煎煮的相对密度,X复方为中药复方煎煮的出膏率,即中药复方中每味饮片的出膏重量之和除以饮片的总取样量,计算方程为:

表2 不同药用部位中药饮片出膏率多重比较结果
①与其他组比较,P<0.05。
①Compared with other groups,P<0.05.

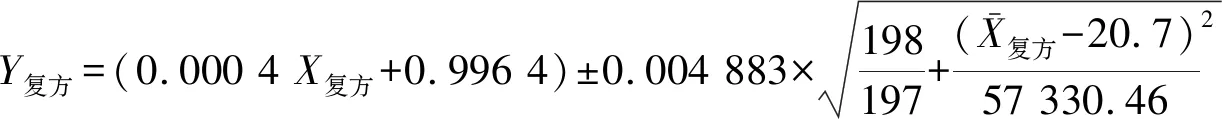
2.3以复方中具体中药饮片煎煮的参数建立数学模型2 以麻杏石甘汤为例进行研究,按照“2.2”项数学模型1建立方法,以复方中具体中药饮片煎煮的相对密度与出膏率建立相对密度预测区间的数学模型。

表3 麻杏石甘汤中4种中药饮片煎煮的主要参数
Tab.3 Main parameters of 4 kinds of TCM decoction pieces in MXSGD
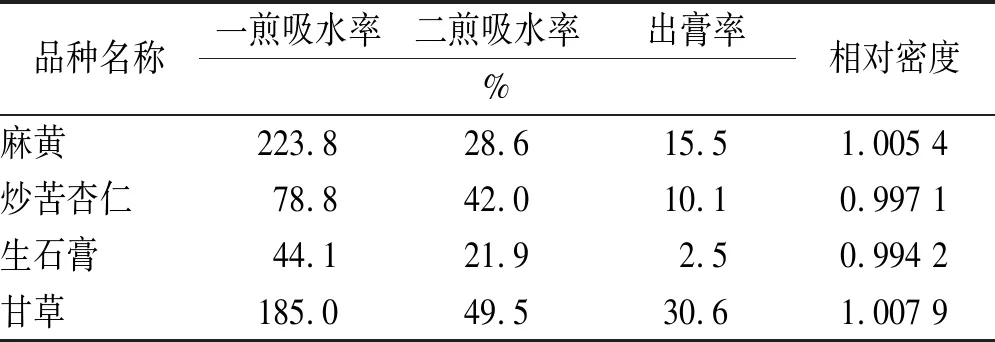
品种名称一煎吸水率二煎吸水率出膏率%相对密度麻黄223.828.615.51.005 4炒苦杏仁78.842.010.10.997 1生石膏44.121.92.50.994 2甘草185.049.530.61.007 9
2.4两种数学模型的验证 取麻杏石甘汤1倍处方量,共3批(每批平行实验2次),分别加水煎煮,一煎加水296.3 mL(一煎吸水量46.3 mL+一煎得液量250 mL),二煎加水263.3 mL(二煎吸水量16.3 mL+二煎得液量250 mL),生石膏先煎30 min,再与其他3味中药饮片一起一煎30 min、二煎20 min,进行验证实验,测定煎煮的得液量、相对密度、出膏率。验证实验结果见表4。
根据表3中每味中药饮片出膏率,利用方程3求得麻杏石甘汤出膏率的理论值X复方=10.9%,代入两种数学模型,求得数学模型1麻杏石甘汤相对密度95%预测区间为(1.000 8±0.004 9),数学模型2麻杏石甘汤相对密度95%预测区间为(0.999 3±0.015 4)。验证实验结果表明,验证实验测定的相对密度(经公式4校正后)均在数学模型1与数学模型2的95%相对密度预测区间之内。
3 讨论
选择麻杏石甘汤作为建立中药复方汤剂煎煮相对密度预测区间数学模型的依据:麻杏石甘汤为《伤寒论》收载的中药解表类经典名方,处方中4种中药饮片分别来源于全草类、种子类、根及根茎类、矿物类等4种不同药用部位,其一日处方剂量为42 g[9],与前期单味中药饮片煎煮50 g的取样量比较接近。
本研究建立的2种数学模型,分别以197种常用单味中药饮片煎煮的参数和以麻杏石甘汤为代表的复方中具体中药饮片煎煮的参数建立相对密度预测区间的数学模型。对于具体的中药复方,数学模型1具有基础数据量大、适用性广等特点。由于数学模型1线性方程决定系数R2=0.879 9,即出膏率中可以解释相对密度变异性的87.99%,另外12.01%的变异不能用相对密度来解释,可能与中药煎煮汤剂中含油脂类成分影响相对密度的测定有关[10]。数学模型2以麻杏石甘汤中具体中药饮片的煎煮参数为基础建立,针对性强,对某一具体中药复方煎煮相对密度预测区间具有灵活性、实用性、个性化等特点。以本研究中麻杏石甘汤为例,数学模型2线性方程的决定系数R2=0.843 3,小于数学模型1决定系数R2=0.879 9,表明数学模型2中相对密度的变异性大于数学模型1中相对密度的变异性。本研究中,数学模型1求得麻杏石甘汤相对密度95%预测区间为0.995 9~1.005 7,数学模型2求得麻杏石甘汤相对密度95%预测区间为0.983 9~1.014 7,数学模型2预测麻杏石甘汤煎煮相对密度的95%预测区间范围大于数学模型1,数学模型2更适合于具体中药复方汤剂煎煮相对密度95%预测区间。
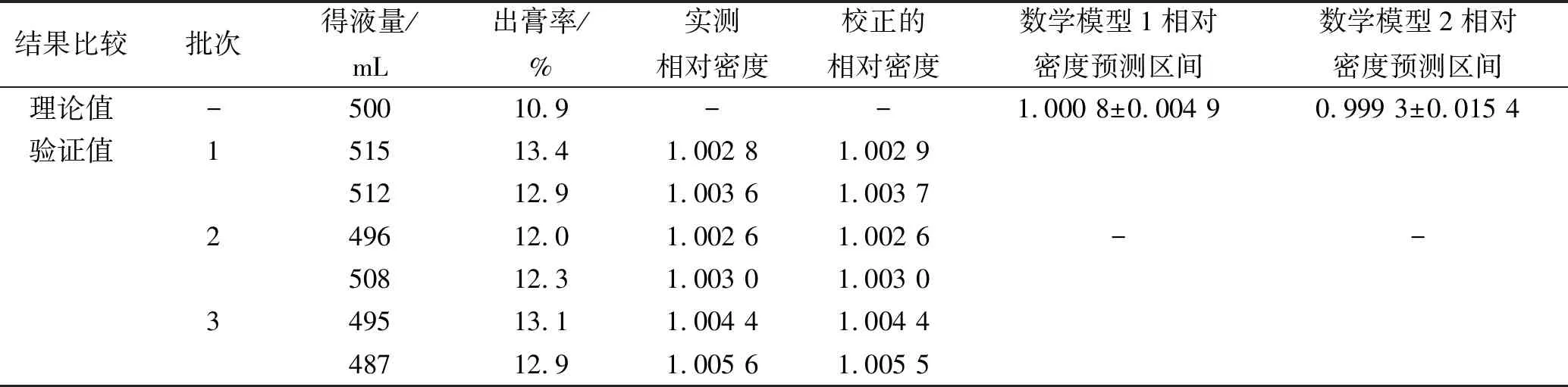
表4 麻杏石甘汤煎煮参数测定及数学模型验证结果
本研究建立的数学模型1基础数据样本量具有一定的局限性,后期本项目组将增加样本量,测定常用近500种中药饮片煎煮的参数,按照建立数学模型1的方法建立中药复方汤剂煎煮相对密度预测区间的数学模型,该数学模型具有适用性广的特点,适用于所有中药复方,但对具体的中药复方汤剂煎煮相对密度预测区间不能体现个性化,代表性和针对性不强。对于临床医生开具的具体中药处方,应用数学模型2的方法即可推导出与具体处方一一对应的相对密度预测区间的数学模型,可更加客观针对性地评价中药复方汤剂煎煮的质量,从而能体现中药复方个性化煎药的质量控制,达到“一人一方”煎药质量评价的目的。
