基于局部保持嵌入-K近邻比率密度的半导体蚀刻过程故障诊断策略
2020-07-15郑百顺郭青秀冯立伟
张 成,郑百顺,郭青秀,冯立伟,李 元
(沈阳化工大学技术过程故障诊断与安全性研究中心,辽宁沈阳 110142)
1 引言
随着现代工业的发展趋势逐渐转向大型化、复杂化,工业系统的安全性和可靠性成为亟待解决的问题.为了有效监控过程健康状态,近年来,深度学习算法及基于数据驱动的多元统计方法已经被广泛应用于生产过程故障诊断领域[1-4].
基于数据驱动的主元分析(principle component analysis,PCA)是一种经典的线性降维算法[5].近年来,以PCA为基础的各类衍生方法相继被提出,如动态PCA(dynamic PCA,DPCA)、贝叶斯融合动态PCA(integrated dynamic PCA,IDPCA)等[6-7].通常基于PCA的一系列方法所获得的低维数据包含原始数据更多有效信息.为了在低维空间中保持原始数据的近邻结构,多种经典的非线性流形算法被提出,如拉普拉斯特征映射(laplacian eigenmaps,LE)、局部线性嵌入(locally linear embedding,LLE)和等距特征映射(isometric feature mapping,ISOMAP)等[8-10].上述方法能够有效提取数据的流形结构,但是它们的非线性性质使其计算量较大[11].因此,He等根据此类缺陷提出了局部保持嵌入(neighborhood preserving embedding,NPE)的算法[11].与PCA相比较,NPE作为一种线性降维算法,能够在低维空间描述原始数据的局部流形结构,对异常值的敏感度低于PCA且适合实际应用[11].然而,NPE与PCA同样应用T2和SPE统计量监控样本状态,文献[12]指出对于多模态和非线性过程,上述统计量不能有效完成状态监控.因此,NPE在监控多模态过程故障时不够完善[13].
针对上述方法的局限性,He等提出的K近邻(K nearest neighbor,KNN)方法被应用到多模态过程故障检测中[12].KNN通过寻找数据近邻特征,有效降低了非线性和多模态特征对故障检测的影响,提高过程故障检测率.然而,KNN方法受方差差异明显的多模态影响会导致故障漏报[14-15].为了提高KNN方法的故障检测率,多种改进KNN方法被提出,但是此类方法都面临耗时长且计算复杂度高的问题[16-17].
针对方差差异显著的多模态间歇过程故障检测问题,本文提出局部保持嵌入-K近邻比率密度(neighborhood preserving embedding-K nearest neighbor ratio density,NPE-KRD)规则的故障检测方法.首先,利用NPE计算负载矩阵将高维数据投影到低维空间;其次,在低维空间计算每个数据点的K近邻比率密度;最后,根据样本的K近邻比率密度统计值进行故障检测.NPE-KRD不但继承NPE保持原始数据局部几何结构的优势,而且通过KRD方法能够有效处理以上多模态过程的故障检测问题.
2 局部保持嵌入(NPE)
假设原始数据集X含有m个样本,n个变量.NPE通过计算负载矩阵A,将高维空间中的m个样本点投影到低维空间,得到新的数据集Ym×d,其中d为数据降维后变量数.
第1步 通过优化式(1),计算权重矩阵W:
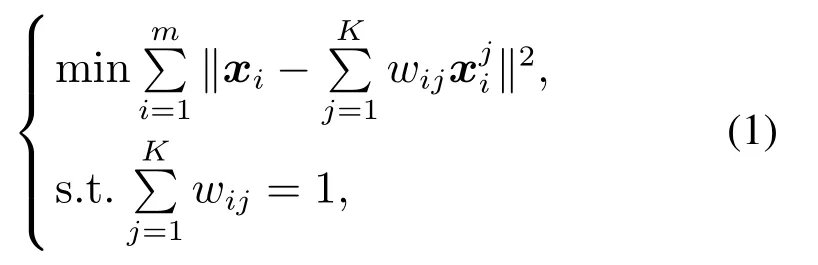
其中:xi为原始样本点为样本xi的第j个近邻,wij为样本点xi与其近邻的关系权重.
第2步 通过式(2)使样本的局部近邻结构得到保持,得到投影矩阵A:

其中yi=xia为样本投影后的点.通过拉格朗日函数法可将最优化求解问题转化为广义特征矩阵中特征值问题,如式(3)所示:
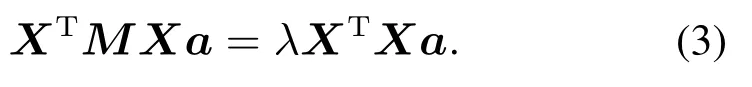
式(3)中l个最小特征值所对应的特征向量构成投影矩阵,即A=(a1,a2,a3,…,al),样本x*投影后可表示为

NPE在过程监控中使用T2和SPE统计量,如式(5)和式(6)所示:
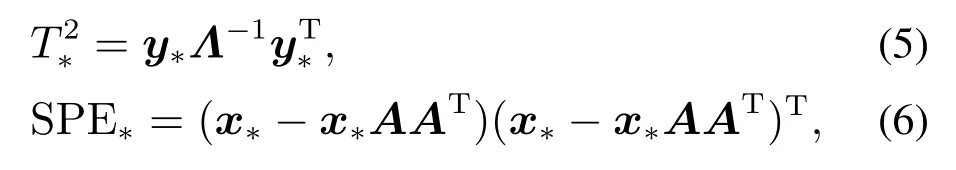
其中Λ是Y 的协方差矩阵,并根据核密度估计法确定T2和SPE统计量控制限[18].
3 基于局部保持嵌入-K 近邻比率密度(NPE-KRD)的多模态故障检测方法
3.1 K近邻比率密度(KRD)
KNN方法通过计算样本与其前K个近邻的距离平方和对过程进行监控.文献[12]指出KNN在处理方差差异较大的多模态过程存在一定缺陷.为了有效监控方差差异显著的多模态过程,本节提出了一种K近邻比率密度(K nearest neighbor ratio density,KRD)的方案.
目前,Rodriguez 提出一种计算局部密度的方法[19],具体过程如下:
首先,计算样本点xi与样本点xj之间的距离如式(7)所示:
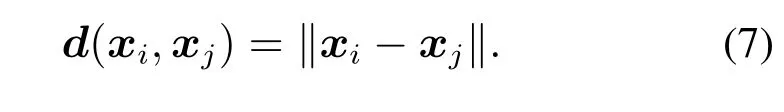
然后,计算样本点的密度ϱi,如式(8)所示:
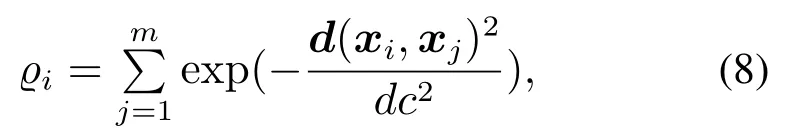
其中:1≤j≤m,j/=i,dc为可按百分比参数求得的截止距离[20].
为了有效监控多模态过程,建立样本的统计量R,如式(9)所示:

由于各模态数据点的密度不同,当正常样本的ϱi较小时,ω也相应较小.当正常样本的ϱi较大时,ω也相应较大.通过计算每个样本的统计指标R,使得各模态中样本点对统计量的贡献度为同一水平且统计值在1附近波动,实现故障样本与正常样本分离的目的.与KNN方法相比较,KRD不仅可以降低多模态方差差异对故障检测的影响,同时还能够有效监控过程密集模态的健康状态.
3.2 基于局域保持嵌入-K近邻比率密度(NPEKRD)的多模态故障检测方法
在多模态故障检测过程中,当样本维数较高时,KRD方法会出现与KNN方法同样的计算量大的问题.因此,先利用NPE方法进行维数约简,接下来在低维空间使用KRD进行故障检测.其故障检测过程分为离线建模和在线检测,如下所示:
离线建模具体步骤:
1) 利用Z-SCORE标准化方法处理得到的数据集X;
2) 利用式(3)计算A,经过式(4)得到降维后的数据集Y;
3) 通过式(9)计算样本yi的KRD统计值R;
4) 根据核密度估计法得到控制限Rα.
在线检测具体步骤:
1) 对测试样本x*进行标准化;
2) 利用式(4)将x*投影到低维子空间中,得到样本点y*;
3) 由式(9)得出y*的KRD统计值R*;
4) 若R*小于Rα,则x*为正常样本;否则,x*为故障样本.
一旦过程发生故障,需要诊断故障发生原因,进而对故障进行准确定位.相对于正常数据,故障数据的分布轨迹与其存在本质上的差异,即当样本密度小于正常样本密度时,判定此样本为故障样本.原因在于样本的某些变量发生变化使之与正常样本偏离.实质上就是故障样本到其第K近邻的距离大于正常样本到其第K近邻的距离.在故障诊断过程中,变量的贡献大是故障生成的主要原因.NPE-KRD诊断过程如下:
首先,在低维空间内计算样本与其第K近邻样本的距离,如式(10)所示:
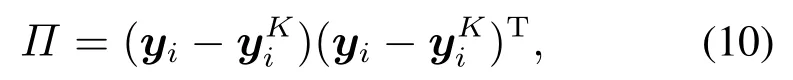
然后,计算变量xj对Π的贡献,如式(11)所示:

4 数值例子
本节应用数值例子对NPE-KRD方法进行说明,模型如下:

其中每个模态均包括4个变量,主要变量为x,y,各模态其余2个变量和e都是微小白噪声.对模型中的两个模态各生成250个样本组成训练集合,同时各生成50个样本组成校验集合,并在密集模态1中通过对变量y增加扰动生成100个故障样本.数据分布特征如图1所示,由图1可知两个模态数据具有不同的分散程度,密集数据源于模态1,稀疏数据源于模态2.
PCA,DPCA,NPE,KNN,KRD和NPE-KRD方法被应用到本节对该例进行故障检测.PCA,NPE及NPE-KRD的主元个数(principal components,PCs)选取为2,DPCA的PCs选取为3,时滞参数为2.本节例子近邻数K选取为3.KRD和NPE-KRD中的dc设定为1.42和0.91.
由图2-4 可知,PCA 和NPE 故障检测率为零,DPCA故障检测率接近于零,主要原因是NPE,PCA和DPCA在故障检测中都假设数据得分服从多元高斯分布,如图5可知PCA得分分布曲线偏离直线轨迹,因此,本例多模态数据得分不满足假设条件.由图6可知,KNN未能有效地在数据中提取出全部故障,主要原因是KNN方法在处理方差异显著的多模态过程时存在缺陷.KRD 和NPE-KRD 故障检测结果如图7 和图8所示,可看出两种方法的故障检测率相近.相对而言,NPE-KRD方法检测效率更高,如图9所示.

图2 PCA检测结果Fig.2 Fault detection results using PCA
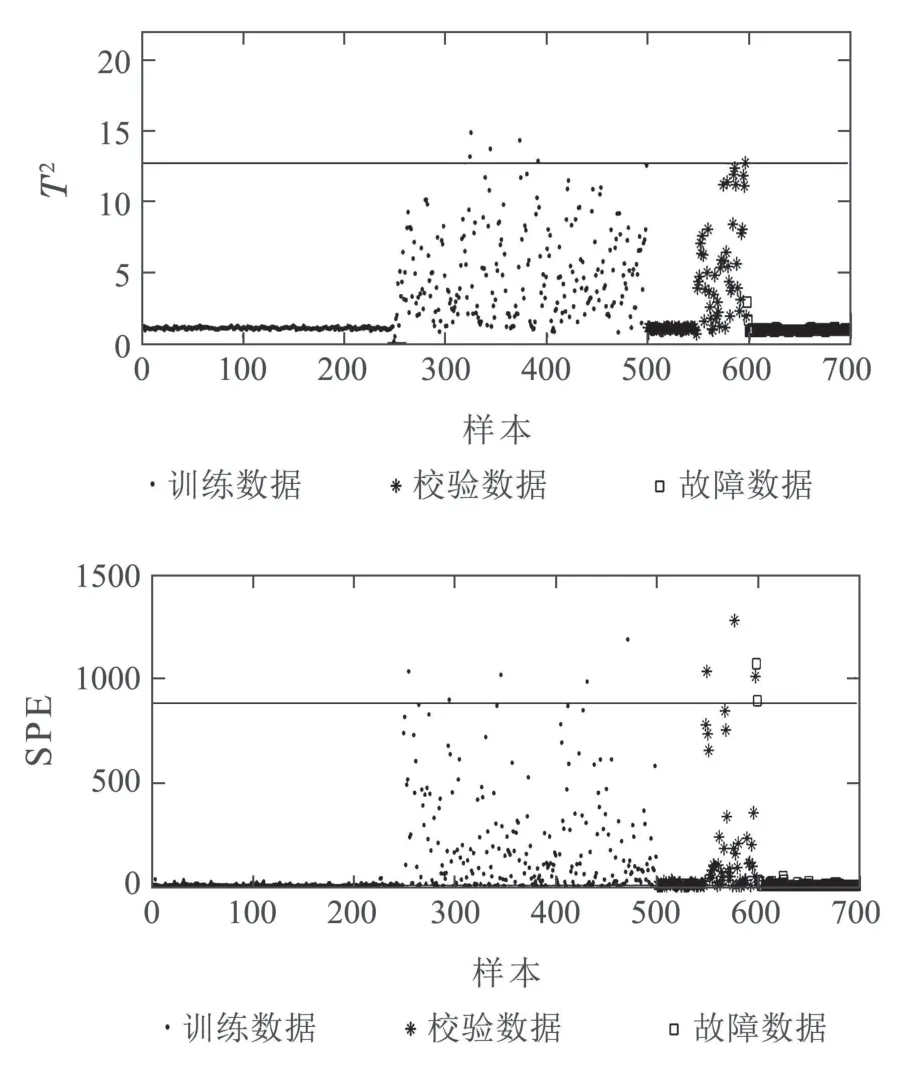
图3 DPCA检测结果Fig.3 Fault detection results using DPCA

图4 NPE检测结果Fig.4 Fault detection results using NPE
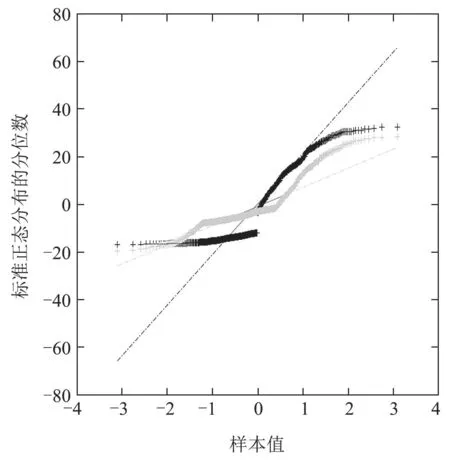
图5 得分变量关系图Fig.5 Relation of score variables

图6 KNN检测结果Fig.6 Fault detection results using KNN

图7 KRD检测结果Fig.7 Fault detection results using KRD

图8 NPE-KRD检测结果Fig.8 Fault detection results using NPE-KRD

图9 KRD与NPE-KRD检测累计耗时Fig.9 Cumulative time of KRD and NPE-KRD
最后,对本例进行故障诊断,结果如图10所示.由图可知在所有变量中变量2的贡献占比较高,因此可判定故障是由变量2发生异常变化所引起.本节中数值例子在变量y(即第2变量)上增加扰动生成故障,结果验证了诊断策略的有效性.

图10 变量贡献图Fig.10 Contribution charts of monitored variables
5 半导体工业过程故障检测实例
本节所应用的半导体数据源于美国德州仪器公司的半导体生产过程[21],数据集包含3个实验过程的108个正常批次、21个故障批次.前34个批次源于第一工况,35到71批次源于第二工况,余下批次源于第三工况.依据文献[22],将正常样本分为训练集和校验集,其中训练集包含101个样本,校验集包含6个样本.应用PCA,DPCA,NPE,KNN,KRD以及NPE-KRD对该过程进行监控,参数设置如表1所示,检测率见表2.
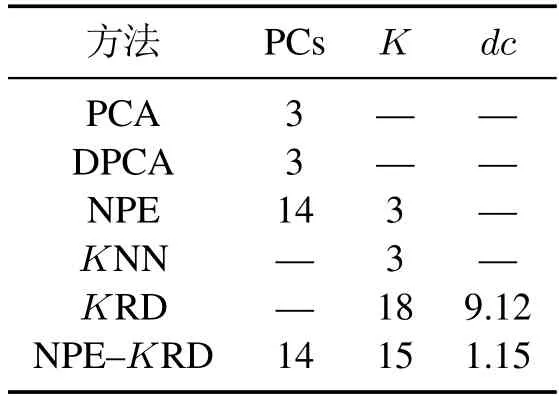
表1 参数确定Table 1 Parameter determinations

表2 故障检测率Table 2 Fault detection rates
由于半导体数据具有多模态特征,而PCA和NPE适用于单模态故障检测,因此检测率较低;此外,3种工况分散程度不同引起KNN具有较低故障检测率.DPCA方法可以有效提取过程动态特征,因而,在半导体工业过程具有较好的故障检测效果.但是本例中的多模态特征仍然制约该方法的监控效果.
相比于KRD方法,NPE-KRD具有更好的故障检测性能,检测率达到100%,如图11-12.主要原因是本文方法利用NPE削弱了离群点的对故障检测的作用,从而提高了故障检测率.

图11 KRD检测结果Fig.11 Fault detection results using KRD

图12 NPE-KRD检测结果Fig.12 Fault detection results using NPE-KRD
本节分别对故障1、故障4和故障10进行诊断,其结果如图13-15所示.针对故障1,可看出变量13具有较大的贡献,因此变量13是故障发生的主要原因.由文献[23]知故障1的故障类型为TCP+50,变量13对应变量名为TCP impedance,符合半导体数据故障设置.同理,故障4和10的异常变量为26和13,分别为变量Chamber Pressure的方差和TCP tuner的均值.诊断结果与文献[23]所述一致.

图13 故障1的变量贡献图Fig.13 Contribution charts of variables for fault 1
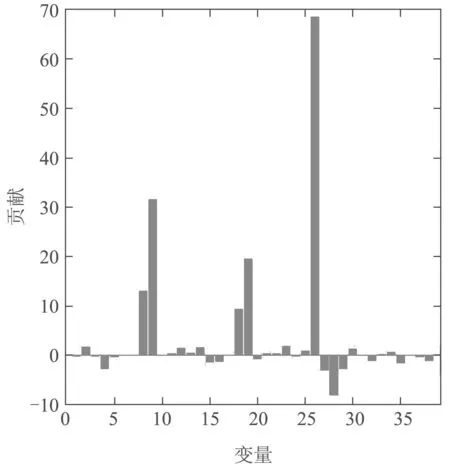
图14 故障4的变量贡献图Fig.14 Contribution charts of variables for fault 4

图15 故障10的变量贡献图Fig.15 Contribution charts of variables for fault 10
6 结论
针对多模态质量监控问题,本文提出了一种基于NPE-KRD的故障检测方法.NPE-KRD不仅降低了故障检测过程的计算复杂度,还提高过程的故障检测率.相比传统的NPE,KNN等方法,本文方法更适合完成模态方差差异显著的过程监控.数值例子及半导体工业过程的仿真实验验证了本文方法的有效性.
