一种粒子势概率假设密度滤波纯方位多目标跟踪算法

张俊根

(北方民族大学电气信息工程学院，宁夏银川 750021)

1 引言

在纯方位多目标跟踪问题中，由于目标信息的不确定性，目标数目每个时刻都会发生变化.此外，目标运动建模与量测建模坐标系转换过程中以及被动传感器自身物理特性造成的模型非线性问题，以及量测信息的不完备性，均给目标跟踪带来了很大困难.如何根据纯方位量测信息对多个目标进行实时、有效地跟踪，一直是学术界和工程应用领域的研究热点和难点问题[1-2].

相对于其他传统的多目标跟踪算法，基于随机集理论的概率假设密度(probability hypothesis density，PHD)滤波算法，可以将复杂的多目标状态空间的运算转换为单目标状态空间内的运算，有效避免了多目标跟踪中复杂的数据关联组合问题[3-6].而势概率假设密度(cardinalized probability hypothesis density，CPHD)滤波算法，能充分利用多目标密度的信息，并且不需要限定目标数目服从泊松分布，受到了更广泛的关注，许多学者开展了相关的研究[7-12].文献[13]基于著名的Faàdi Bruno行列式，推导了CPHD模型中的衍生目标广义势分布预测方程，提出了一种通用势分布预测方程的可处理递推计算方法.文献[14]研究了基于最适高斯近似和强跟踪的多模型伽马高斯逆威夏特-概率假设密度滤波的群跟踪算法，能有效处理群目标的合并和衍生情况.文献[15]针对扩展目标跟踪问题，提出了一种扩展的标记箱粒子CPHD滤波器，可以改善目标数目估计的精度，同时能获得目标的轨迹.文献[16]针对多传感器多目标跟踪中的分布式传感器控制问题，利用随机有限集进行建模，提出一种基于多目标战术重要性评估的多传感器控制策略.

本文针对混合线性/非线性目标状态模型，将CPHD和Rao-Blackwellised的思想[17]有效结合起来，提出一种新的混合粒子滤波CPHD实现算法，将目标状态划分为线性和非线性这两种结构信息，线性状态信息利用卡尔曼滤波(Kalman filter，KF)，非线性状态信息利用粒子滤波(particle filter，PF)，对多目标的概率假设密度和势分布进行预测与估计，再运用Mean-Shift方法提取目标状态估计值，并对算法的复杂度进行了推导和分析，最后，将算法应用到多传感器纯方位目标跟踪场景中，仿真实验结果表明，所提出的算法能够实现对目标数和目标状态的准确估计，改善目标跟踪精度.

2 问题描述

2.1 随机集纯方位多目标跟踪问题

考虑下面的被动多传感器纯方位多目标跟踪系统:

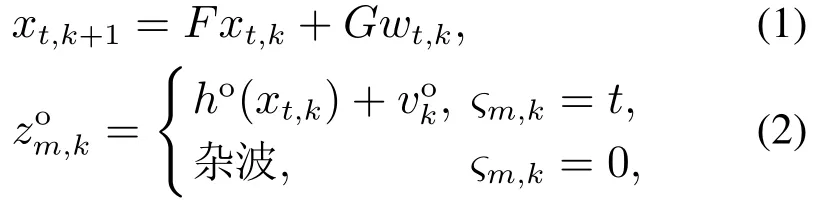
在随机集多目标跟踪问题中，多目标的状态和传感器量测可以建模为随机有限集的形式[3]，即Xk={xk，1，…，xk，Nk}∈F(X)为目标状态集，Zk={zk，1，…，zk，Mk}∈F(Z)为量测集，其中:F(X)和F(Z)分别是X和Z上的所有有限子集的集合;Nk及Mk分别表示k时刻目标个数及量测个数，其中某些量测可能源于杂波.

若k-1时刻状态随机集为Xk-1，则k时刻的状态随机集Xk可表示为

其中:Γk表示k时刻新生目标状态随机集;Bk|k-1(x)表示k时刻从目标x衍生分裂出来的目标状态随机集;Sk|k-1(x)表示从k-1时刻到k时刻仍然存活的目标状态随机集.

目标的量测随机集Zk可表示为

其中:Kk表示虚警或杂波量测随机集;Θk(x)表示源于真实目标的量测随机集.

2.2 CPHD滤波

相比于PHD滤波，CPHD滤波联合估计目标强度和势分布(即目标数n的概率分布)，可以改善状态估计性能[7].

令Dk|k-1和pk|k-1分别表示k-1时刻预测多目标强度和势分布，Dk和pk表示k时刻后验多目标强度和势分布，则CPHD迭代公式为

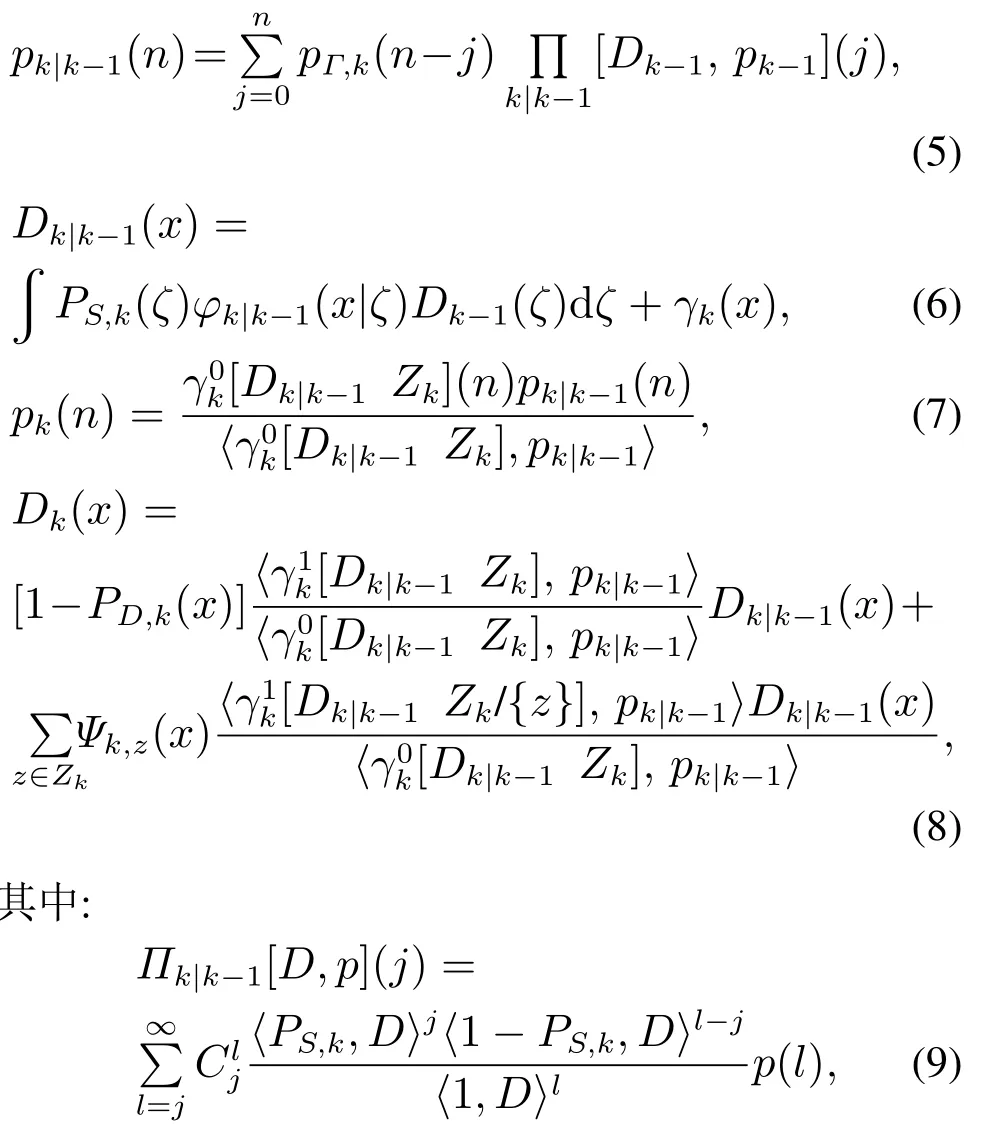
其中:N(x;m，P)表示均值为m、协方差为P的高斯密度，Qk-1是过程噪声协方差，Rk是量测噪声协方差.

3 多目标跟踪粒子CPHD滤波

在很多应用中，目标状态空间包含线性和非线性两部分，针对这类混合线性/非线性状态模型，利用贝叶斯原理将线性状态从系统模型中分离出来，并结合卡尔曼滤波器和粒子滤波器对目标的线性状态和非线性状态分别进行估计[17]，本文结合RBPF的思想，估计出多目标PHD和势分布，由于多目标跟踪的复杂性，使得迭代估计所得的PHD形状很不规则，运用Mean-Shift方法，可以提取出精确的密度函数峰值位置[18]，可以提高目标跟踪精度，减小估计方差.

3.1 算法描述

假定目标不发生衍生，各个目标的动态系统同时存在线性和非线性的状态，且噪声是加性的，那么目标滤波模型可以表示为线性和非线性的形式:

且wk与vk相互独立.

算法由预测和更新两部分构成:

预测:假定已知k-1时刻的多目标后验概率假设密度Dk-1和势分布pk-1，并且Dk-1可以用一组带权值的粒子来表达:

为了得到Dk|k-1的粒子近似，对式(22)中的每一项都运用Rao-Blackwellised方法进行混合滤波.首先，对于存活目标，由式(19)预测非线性状态粒子

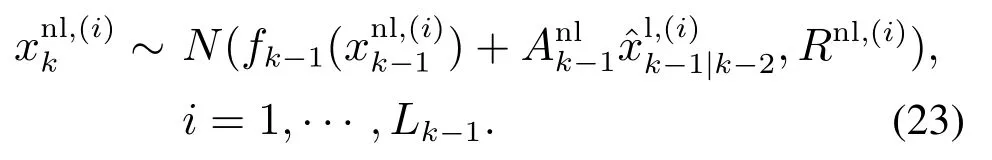
线性状态粒子可由KF方程获得

其中

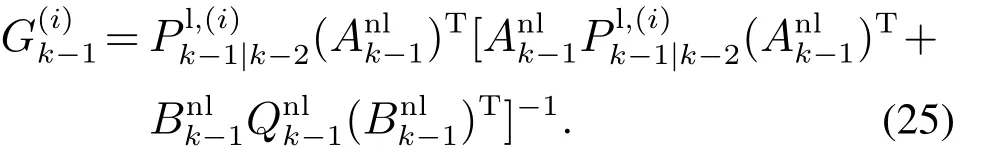
计算粒子的权值

势分布pk|k-1(n)通过式(5)来计算.

更新:已知k-1时刻的多目标预测概率假设密度Dk|k-1和势分布pk|k-1，并且Dk|k-1可由粒子来描述.运用KDE理论[19]可得多目标随机集的更新PHD:

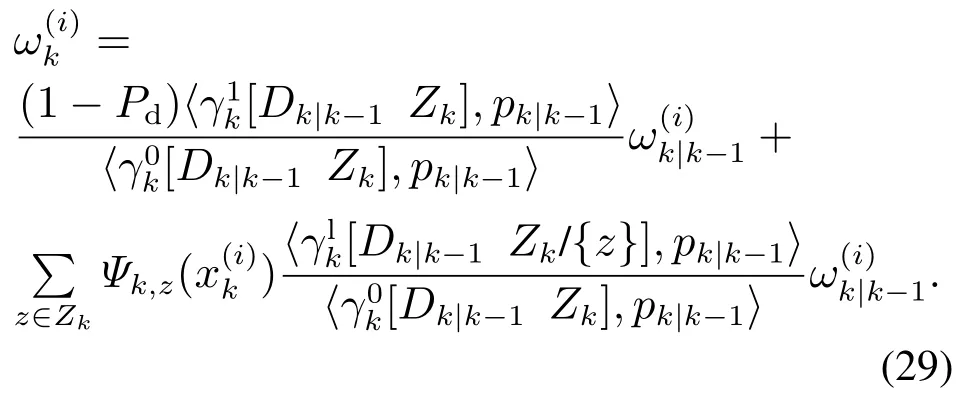
势分布pk(n)利用式(7)计算.

目标数的估计为

利用Mean-Shift算法，提取密度函数所有的峰值位置.对于粒子其Mean-Shift向量为

本文所提算法:最密集的位置，即

1) 给定Dk-1和pk-1

预测:

2) 对于i=1，…，Lk-1，利用式(23)计算

7) 根据式(5)预测势分布pk|k-1.

更新:

9) 根据式(28)估计目标强度函数Dk;

10) 利用式(7)更新势分布pk，并利用式(31)估计目标数nk;

3.2 算法复杂度分析

这一小节引入等效浮点运算(equivalent flop，EF)测度来分析算法的复杂度[21]，一个运算的EF复杂度定义为浮点运算(flops)的数量，这里一次浮点运算表示两个浮点数的一个加、减、乘或除.从算法描述看出，算法的计算量主要体现在更新步骤，其中包括漏检目标和检测目标的粒子似然比的计算[8]、粒子Mean-Shift向量的计算以及重采样的计算，对于每次时间迭代，算法更新步骤总的加法或乘法次数可以表示为量测数Mk的一个多项式

其中:Lk表示k时刻的粒子数，Nmax为最大目标数，系数c1，c2，c3分别用来等效高斯似然、Mean-Shift向量以及重采样的计算复杂度.

从式(33)可以看出，在给定最大目标数Nmax的情况下:1)随着量测数的增大，算法复杂度呈三次方增长;2)随着粒子数的增大，算法复杂度呈二次方增长.利用门选技术，删除一些不相关的量测，可以减小算法的计算量.

4 仿真实验与分析

对所提算法进行性能仿真实验，利用目标数估计的统计值和OSPA距离评价算法的性能，并与PFCPHD，RBPF-PHD这两种滤波算法作对比.

系统模型如式(1)-(2)，其中目标数随时间变化，假设有3个被动传感器对目标进行纯方位跟踪，假定各传感器的量测数据已完成配准及关联.系统具体参数设置如下:

采样周期Ts=1 s;目标系统矩阵

过程噪声Q=diag{[0.01 0.01]};3个传感器位置分别为(-8，-10)km，(8，-10)km和(8，13.86)km.

被动传感器对目标只能测得方位角，量测函数

其中:(xo，yo)是传感器位置，量测噪声标准差都设为σβ=0.01，目标存活概率Ps=0.99，检测概率Pd=0.98.

新生目标随机集的强度函数为

其中:

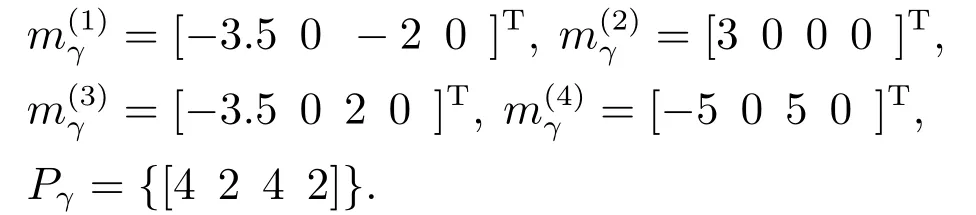
杂波均匀分布于量测空间，数目服从参数为λ=3的泊松分布;OSPA距离参数p=2，c=100;粒子数500，仿真次数为100.

图1为多目标在x和y方向上的运动轨迹，图2为各算法目标数估计均值，图3给出了各算法目标数估计标准差.可以看到，PF-CPHD，RBPF-PHD和本文算法的目标数估计都能收敛到真实值，RBPF-PHD 滤波算法对目标数的估计能较快收敛;本文算法对目标数估计的方差最小，表明所提算法的目标数估计要更加可靠.另外，从图2可知，当目标数发生变化时，PFCPHD和本文算法对目标数的估计具有较大的延时，而RBPF-PHD滤波算法的目标数估计延时较小，原因主要在于RBPF-PHD滤波算法的目标数估计方差较大，估计的结果不可靠，导致滤波器更容易受新来量测的影响，响应较快.

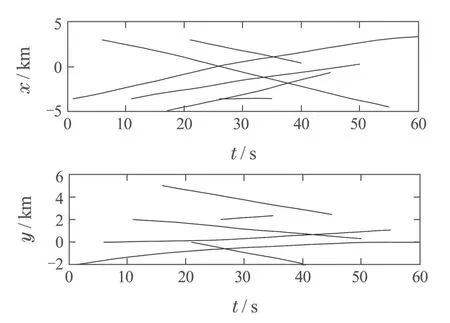
图1 实际的目标运动轨迹Fig.1 The true target tracks in x and y-coordinates

图2 目标数估计均值Fig.2 The estimated mean of cardinality

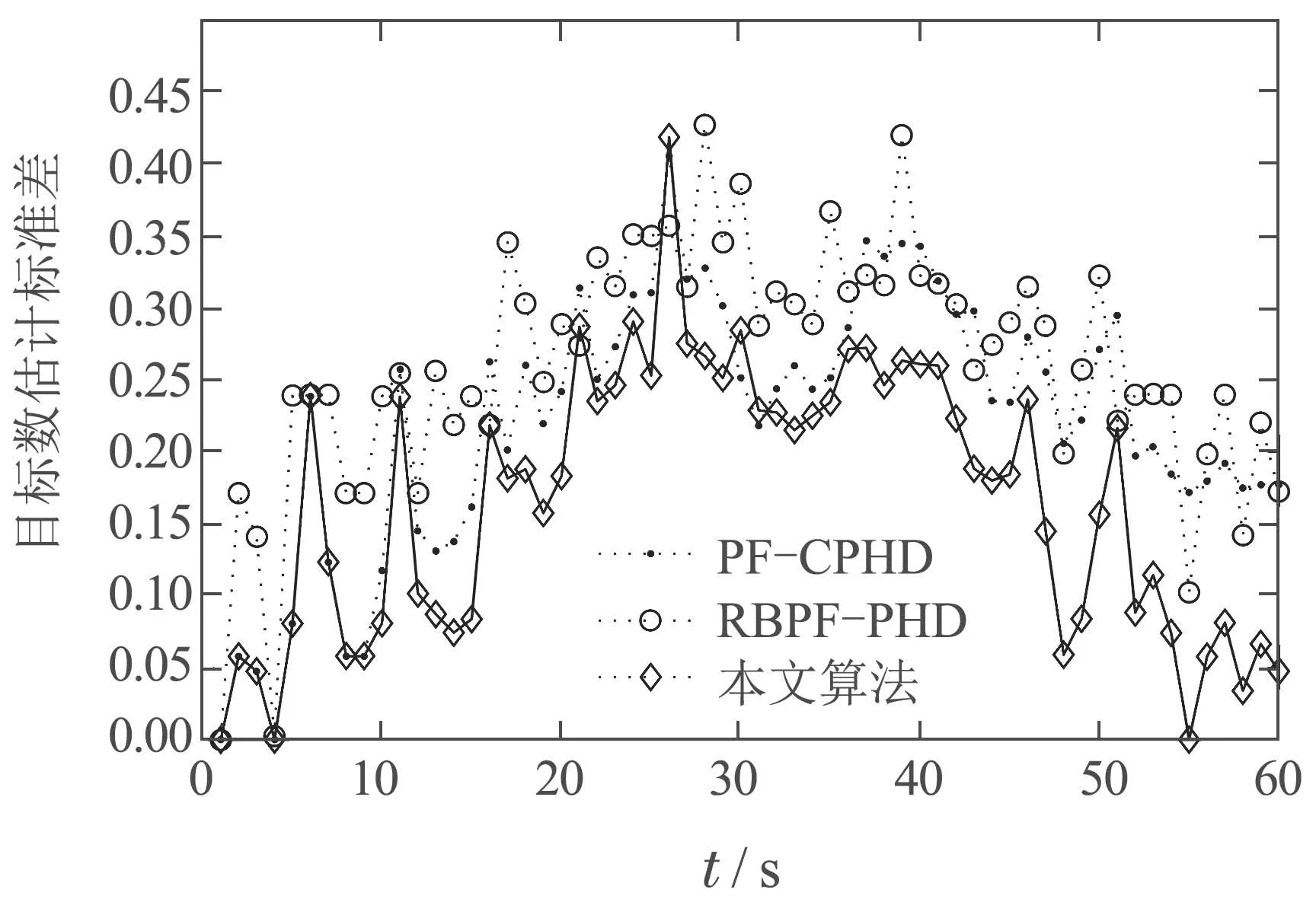
图3 目标数估计标准差Fig.3 The estimated STD of cardinality

图4给出了3种算法目标跟踪的OSPA距离.可以看出，在多数时刻，本文算法的跟踪误差比PF-CPHD和RBPF-PHD滤波算法都要小;在目标数发生变化的时候，RBPF-PHD算法的跟踪精度要好于另外两种算法，主要原因是PF-CPHD和本文算法在目标数发生变化时，对目标数的估计存在较大的延时，OSPA距离惩罚的程度比RBPF-PHD滤波算法要大;而在目标数稳定以后，本文算法的OSPA距离相对较小.

图4 目标跟踪的OSPA距离Fig.4 100 MC average OSPA distance

图5给出了这3种算法的平均OSPA距离随粒子数变化的对比.可以看出，本文算法的平均OSPA距离比PF-CPHD 和RBPF-PHD 算法都要小;当粒子数由300增大到500时，RBPF-PHD滤波算法的平均OSPA距离有较大的改善，当粒子数继续增大时，性能改善不明显;PF-CPHD和本文算法随着粒子数的增大，平均OSPA距离都将减小.当然，随着粒子数的增多，各算法的运算时间也将增大.图6给出了3种算法平均运算时间对比，本文算法由于要联合估计目标强度及目标数的概率分布，并且运用了Mean-Shift算法进行状态提取，运算量较大.

图5 各算法的平均OSPA距离对比Fig.5 Comparison of the mean of MC average OSPA distance

图6 各算法的平均运算时间对比Fig.6 Comparison of average operation time

为了验证本文算法的复杂度与量测数的关系，对仿真实验重新设计，假定目标数不随时间变化，通过增大目标数来增大量测数，杂波强度设为3，粒子数为500，其他仿真参数不变，算法复杂度用运算时间来代表.图7给出了本文算法的平均运算时间与量测数的关系，为便于对比分析，图中画出了一个关于量测数的三次方曲线方程.可以看出，本文算法复杂度由于与多个参量有关系，与量测数近似满足随着量测数的增大复杂度呈三次方增长的关系.

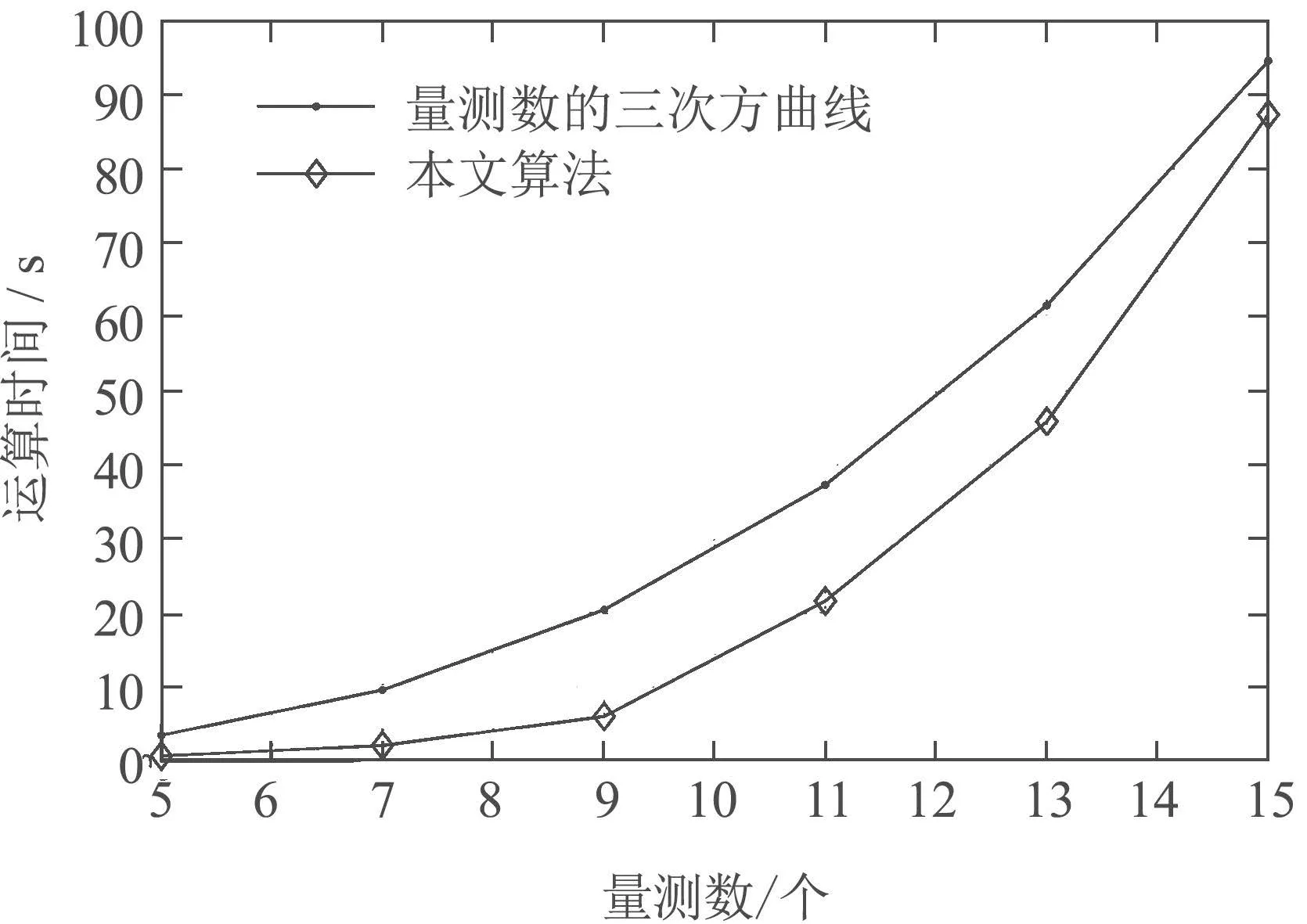
图7 本文算法平均运算时间与量测数的关系Fig.7 The relationship between the average operation time and the number of measurements

5 结语

本文针对混合线性/非线性目标状态空间跟踪模型，提出了一种多传感器纯方位多目标跟踪粒子CPHD滤波算法，通过挖掘混合线性/非线性状态模型的结构信息，结合PF与KF对各个目标的状态进行预测与估计，以便更好地估计目标强度函数及势分布，运用Mean-Shift算法提取多目标密度函数的峰值作为目标状态估计值，并分析了算法的复杂度，仿真结果验证了算法的有效性.算法虽然提升了跟踪精度，但带来的计算复杂度较高，如何利用被动传感器的分布式计算来减小算法的运行时间，将是后续研究的方向.