改进人工蜂群算法求解模糊柔性作业车间调度问题

郑小操，龚文引

(中国地质大学(武汉)计算机学院，湖北武汉 430074)

1 引言

调度在生产系统的决策和现代制造业中资源的分配中都起着至关重要的作用[1].柔性作业车间调度问题(flexible job shop scheduling problem，FJSP)是现今许多实际问题的抽象，具有很强的现实意义，因此一直是运筹学领域研究的热点.FJSP是由车间调度问题(job-shop scheduling problem，JSP)发展而来的，是一种典型的非确定性多项式(nondeterministic polynomial，NP)难问题.对于传统的作业车间调度问题，工序在加工过程中可选择的机器只有一个，而FJSP中有的工序可能有多个机器可供选择，这更符合现代制造业和交通运转的实际特点.因此在对FJSP进行求解的过程中不仅要考虑工序的加工顺序问题，还要考虑机器的选择问题.所以FJSP要比传统的JSP要复杂得多.

FJSP在现代制造业和智能交通系统的调度中都起着至关重要的作用.近些年来，群智能算法和智能技术得到了迅猛的发展，这些方法被广泛应用于FJSP的求解中，Nouiri等[2]提出了一种高效的分布式粒子群算法来求解FJSP，该算法以最小化最大完工时间为目标，并通过多个标准数据集验证了算法的有效性.针对工序可重叠的FJSP，Meng等[3]设计了一种混合人工蜂群算法，并通过实验证明了改进算法具有良好的收敛性.李等[4]提出了一种新型的帝国竞争算法来解决高维多目标柔性作业车间调度问题，该算法采用新方法构建初始帝国使得大多数殖民国家分配数量相近的殖民地.Gao等[5]提出的离散和声搜索算法同样能非常高效地求解FJSP.

现实中的调度问题是多种多样的，不同调度问题的结合，又能产生许多复杂多样的调度问题.在实际进行调度的过程中，可能会遇到一些突发情况和一些实际需求，例如机器出现故障[6-7]、绿色低碳调度[8-10]、工件在加工的过程中需要消耗资源[11]、在调度的过程中有运输约束等[12-13]，由此又可以形成许多实时调度问题.还有许多多目标调度问题[14-15]、分布式车间调度问题[16].在这些复杂多样的调度问题中，工序在机器上加工的时间往往是一个确定的值，但是在实际的生产调度过程中，工序加工的时间往往是不确定的.例如在搭乘高铁的时候，有些车次会出现晚点的情况.机器在运转的过程中会发生故障等.因此，加工和运行时间的模糊性是现代制造业和交通系统调度中的一个普遍特点，具有很重要的研究价值.Sakawa等[17]首次采用遗传算法(genetic algorithm，GA)来求解模糊作业车间调度问题，采用了三角模糊数来表示加工的时间，并通过特定的规则来进行三角模糊数的运算.模糊柔性作业车间调度问题(fuzzy flexible job-shop scheduling problem，FFJSP)是FJSP与模糊作业车间调度问题的结合[18]，FFJSP更加符合实际生产调度的需求.许多研究者针对FFJSP做了大量的研究.Lei提出了一种协同进化的遗传算法(co-evolutionary genetic algorithm，CGA)[19]能非常高效地求解FFJSP.该算法应用了一种新颖的交叉操作和改进的锦标赛选择策略.Wang等[20]设计了一种高效的分布式估计算法(estimation of distribution algorithm，EDA)，在解码的过程中采用了左移策略，很好地利用了机器的空闲等待时间.Gao等[21]提出了一种离散和声搜索算法(discrete harmony search algorithm，DHS)来求解FFJSP，该算法提出了一种有效的启发式规则来初始化和声库.Huang等[22]采用6种启发式规则来初始化工序序列，提出了一种改进的离散粒子群算法(improved discrete particle swarm optimization，IDPSO)求解FFJSP.

人工蜂群算法(artificial bee colony algorithm，ABC)[23]是一种新颖的群智能算法，因其具备良好的优化性能以及需要设定的参数较少[24]，所以一直以来都是研究者们研究的热点.Sharma等[25]提出了一种啤酒泡沫人工蜂群算法(beer artificial bee colony algorithm，BeFABC)来求解JSP，该算法在观察蜂阶段，将啤酒泡沫现象引入到位置更新的过程中，这样可以很好地平衡算法的勘探与开采能力.Wang等[26]设计了一种高效的ABC来求解FJSP，该算法在观察蜂阶段采用基于关键路径的局部搜索(local search，LS)来改善蜜源.Gao等[27]采用分两阶段的人工蜂群算法来求解有新工件插入的柔性作业重调度问题，该论文提出了一种高效的机器选择策略.针对FFJSP，Wang等[28]提出了一种混合人工蜂群算法(hybrid artificial bee colony algorithm，HABC)，该算法采用多种策略来初始化种群，并且通过变邻域搜索来提升算法的局部搜索能力.Gao等[29]设计了一种改进的人工蜂群算法(improved artificial bee colony algorithm，IABC)求解FFJSP，该算法以最小化最大模糊完工时间和机器总负载为优化目标.

现有的求解FFJSP的算法往往存在着一定不足，例如需要设定的参数较多，初始种群的多样性太低，局部搜索能力较差等.针对这些缺点和不足，本文提出了一种基于邻域搜索(neighborhood search，NS)的ABC，该算法以最小化最大模糊完工时间为目标.首先采用混沌初始化的方式来初始化种群，保证了种群的多样性.然后利用4种邻域结构对种群中的个体进行邻域搜索，以此来增强其局部搜索能力.并且提出了一种新颖的交叉策略，使种群中的个体总是与种群最优个体进行交叉，这样既可以有效地改善当前个体的适应度值，又能加快种群的收敛速度.在解码的过程中采用左移策略，尽可能地利用机器上的空闲时间，能有效地减小最大模糊完工时间.通过实验验证了本文算法具有良好的优化性能.

2 模糊柔性作业车间调度问题

2.1 问题描述

FFJSP一般由n个工件Ji(i=1，2，3，…，n)和m台机器Mk(k=1，2，…，m)组成，每个工件Ji包括hi道工序，工序Oij表示工件Ji的第j道工序.每道工序可以在一台或多台机器上进行加工.工序在机器上加工的时间用三角模糊数tijk=(t1，t2，t3)表示，其中t1表示工序最早能完成的时间，t2表示工序最有可能完成的时间，t3表示工序最晚完成的时间.hi表示工件Ji的总工序数.FFJSP的优化目标是最小化最大模糊完成时间，这个时间是三角模糊数，如下式所示:

其中:CM表示最大完成时间，Ci是工件Ji的完成时间.表1展示了一个规模为3个工件，3个机器的FFJSP实例.表中的各行代表的是工序，各列表示的是机器.表中的条目是各工序在相对应的机器上加工的模糊时间.O11对应的是第1个工件的第1道工序.

表1 规模为3×3的FFJSP实例Table 1 Example of FFJSP

2.2 三角模糊数的运算

对于FFJSP，所涉及的三角模糊数的操作包括3种:加法操作，比较操作和模糊取大操作[1].给定两个三角模糊数:A=(a1，a2，a3)，B=(b1，b2，b3).

加法操作如下所示:

比较操作:

1) 如果

则A ＞B，反之A ＜B.

2) 如果F1(A)=F1(B)，则当

A ＞B，反之A ＜B.

3) 如果F2(A)=F2(B)，则当

A ＞B，反之A ＜B.

模糊取大操作:

如果A ＞B，则A ∨B=A，反之A ∨B=B.

3 引入邻域搜索的人工蜂群算法

3.1 人工蜂群算法

人工蜂群算法(ABC)[23]是一种新颖的群体智能算法，它的基本思想来源于自然界中蜜蜂的觅食过程.在ABC中总共有3类蜜蜂:雇佣蜂、观察蜂和侦查蜂.每个蜜源代表一个可行解，蜜源的质量对应可行解的适应度[30].ABC的主要步骤如下:

1) 初始化参数和种群阶段.

ABC的参数有:蜜源的个数(SN)，控制次数(limit)，雇佣蜂和观察蜂的数目，假设蜜源的维度为n，蜜源的产生如下所示:

式中:j∈{1，2，…，n}，i∈{1，2，…，SN}，Xij对应的是第i个蜜源，第j维的变量，r1是范围为(0，1)的随机数，Ubj，Lbj分别是第j维变量的上界和下界.

2) 雇佣蜂阶段.

在雇佣蜂阶段，每个雇佣蜂会在与之对应的蜜源附近产生一个新的蜜源，如下所示:

其中:j∈{1，2，…，n}，k∈{1，2，…，SN}且k/=i，r2是[-1，1]中均匀分布的实数，如果新蜜源的适应度值优于或等于原蜜源的适应度值，则新蜜源取代原蜜源.否则保留原蜜源.

3) 观察蜂阶段.

观察蜂通过概率Pi选择一个蜜源Xi进行操作，Pi的计算式如下所示:

式中:fi表示蜜源Xi的适应度值，蜜源的适应度值越大，被选择的概率就越大.蜜源被选择后，通过式(4)得到一个新蜜源，如果新蜜源的适应度值大于或等于Xi的适应度值，则新蜜源替代Xi.

4) 侦查蜂阶段.

如果蜜源Xi经过limit次迭代操作后都没有改进，则舍弃这个蜜源并启用侦查蜂.侦查蜂通过式(3)产生一个新蜜源.

3.2 编码与解码

本文的编码采用基于工序的编码.假设表1的FFJSP实例的一种基于工序的编码为(1 2 1 3 1 3 2)，其中的第1个数1表示的是第1个工件的第1道工序，第2个数2表示的是第2个工件的第1道工序，第3个数1表示的是第1个工件的第2道工序.在机器的选择中，采用最小完成时间原则[31].计算工序在其所有可选机器上的完成时间，选择完成时间最小的机器对该工序进行加工.所以一旦工序码改变了，有些工序所选择的机器将会随之改变.

为了提升解码性能，本文采用左移策略[32]，通过这种策略，尽可能利用机器空闲的时间段，从而减小最大完工时间.左移策略的操作如图1所示.图1针对的是表1中的具体实例的一种调度方案，在解码的过程中，大多数采用的是后接的方式，也就是在所选机器的最后一道工序的后面进行加工.例如图1中工序O32，如果选择机器2进行加工，它将接在O22的后面，则其完成时间为(17，24，28).如果选择机器3进行加工，它将接在O12的后面，则O32完成时间为(20，27，29).如果选择第3个机器进行加工，它将接在O22的后面，则O32完成时间为(17，24，28).如果采用左移策略进行解码，在机器1中，在O21和O13之间有足够大的空闲时间可供加工O32，此时O32的完成时间为(4，9，12)，通过这种解码方式，可以有效地减小最终的最大完工时间.

图1 通过左移策略进行解码Fig.1 Decoding by left-shift scheme

假设工序Oi，j需要在机器M上进行加工，且加工时间为T，M中存在空闲时间段为[tS，tE]，tS是空闲开始时间，tE是空闲结束时间.工序Oi，j的前一道工序Oi，j-1的完成时间为Ci，j-1.如果满足式(6)的条件，则工序Oi，j可以安排在M的空闲时间段[tS，tE]内进行加工.

3.3 种群初始化

在用启发式算法求解多元问题时，初始种群的质量往往对种群的收敛速度以及最终的结果影响非常大，因此生成一个高质量的初始种群非常关键.本文采用混沌初始化的方式来进行种群初始化[33].

混沌是非线性动力学系统中的一种运动形式，具有随机性，遍历性及对初始值敏感性的特点[34].采用混沌初始化可以使初始种群的个体离散地分布在解空间内，能够非常有效地提高种群的多样性.在众多的混沌系统当中，Logistic 混沌映射是最典型的混沌系统.Logistic混沌映射的系统方程如下:

式中 X(k)是混沌变量，它的取值范围是(0，1)，当u=4时，系统处于完全混沌状态.混沌初始化的步骤如下:

步骤1随机生成与总工序数相等数目的混沌变量，如表2所示.表2中所有工件的总工序数为7，所以随机生成7个混沌变量.混沌变量序列与工序序列一一对应.

步骤2将混沌变量序列按从小到大的顺序排列.

步骤3将原来与混沌变量相对应的工序随之移动，例如混沌变量0.65与工序O11对应，0.65经过升序排列后位置为5，所以将工序O11也移动到第5位.

步骤4将变动后的工序序列生成对应的工序码.

通过以上过程便可以生成一个工序序列，将以上操作的混沌变量序列的每一维经过式(7)的变换生成新的混沌变量序列，然后继续上面的步骤就可以生成第2个工序序列，以此类推，就可以完成种群初始化的过程.

表2 初始化工序序列过程Table 2 Proceure of initial operation sequence

3.4 邻域搜索

在利用群智能优化算法求解组合优化问题时，邻域搜索是一种非常简单有效的元启发式算法.通过对一个个体进行交换、插入、逆转等操作，可以发掘出该蜜源附近更加优质的蜜源，提高算法的局部搜索能力.本文主要采用了4种邻域结构.

1) 邻域结构N1:随机在工序序列中选择工序码不同的两道工序进行交换.

2) 邻域结构N2:在工序序列中随机选择两道工序，将这两道工序之间的工序进行逆转.

3) 邻域结构N3:随机选择一道工序，将这道工序与其后面的工序进行交换.如果这道工序是工序序列中的最后一道工序，则重新选择.

4) 邻域结构N4:在工序序列P中随机选择一个工序O，将其抽离出来形成P1，然后将O插入到P1中所有能插入的位置，形成多个不同的蜜源，取所有蜜源中最优的蜜源.

以上操作按序进行，如果采用邻域结构N1形成的新蜜源优于当前蜜源，则将新蜜源取代当前蜜源，然后继续采用邻域结构N1，直到不能改变当前蜜源时转向下一个操作.

3.5 交叉操作

交叉操作可以交换两个个体之间的信息，能在一定程度上避免个体陷入局部最优.由于每个工件的工序数是确定的，所以不能像实数域中的交叉方式那样直接交换两个工序片段，文献[27]中提出了一种新的交叉策略:随机生成一个小于最大工件数的正整数N，将当前个体中小于或等于N的工序码固定不变，将大于N的工序码移除.然后将与之交叉的个体中的大于N的工序编码依次填入当前个体.这种交叉策略可操作的范围太小，如果有10个工件，最多只有9种情况.根据这种交叉策略，本文提出了一种新的交叉方法，在这种方法中，当前个体总是与种群最优个体进行交叉.如图2所示.交叉操作的步骤如下:

步骤1随机确定需要固定的工件数目，图2中需要固定的工件的数目为3.

步骤2随机确定固定的工件编号，图2中需要固定的工件为3，4，5.

步骤3移除编号不是3，4，5的工序码.

步骤4将全局最优个体中编号不是3，4，5的工序码依次填充到当前个体中.

通过这种交叉方法，可以生成两个新蜜源，取这两个新蜜源中较好的蜜源与当前蜜源进行比较，如果新蜜源优于当前蜜源，则将其替换.

图2 交叉操作Fig.2 Crossover operation

3.6 算法流程

引入NS的ABC在求解FFJSP时，采用混沌初始化的方式来初始化蜜源，以此来提高初始蜜源的多样性.蜜源的编码采用的是基于工序的编码，在解码的过程中，通过左移策略来提升解码的性能.为了提高算法的局部搜素能力，引入了NS，采用4种邻域操作来发掘当前蜜源附近的优质蜜源.通过交叉操作进一步提高蜜源的质量，加快种群的收敛速度，在一定程度上避免蜜源陷入局部最优.算法的基本流程如下:

步骤1设置参数，包括蜜源的数目，雇佣蜂的数目，观察蜂的数目以及控制次数(limit).其中蜜源的个数与雇佣蜂的数目相等.

步骤2采用第4.2节中的混沌初始化方法初始化蜜源，并计算各蜜源的适应度值，求出最优蜜源.

步骤3雇佣蜂阶段，对于所有的个体，重复以下步骤:

1) 对于每一个蜜源，采用第4.3节中的邻域搜索发掘出当前蜜源附近的优质蜜源;

2) 通过第4.4节中交叉操作进一步优化当前蜜源.

步骤4观察蜂阶段，对于所有个体，重复以下步骤:

1) 采用锦标赛选择法选择一个蜜源;

2) 采用第4.3节中的邻域搜索发掘出该蜜源附近的优质蜜源;

3) 通过第4.4节中交叉操作进一步优化当前蜜源.

步骤5侦查蜂阶段，如果一个蜜源经过limit次迭代操作后还没有改进，则重新初始化一个蜜源.

步骤6如果达到了最大迭代次数，就终止算法，输出最优蜜源.否则返回到步骤3.

3.7 算法复杂度分析

本文算法在迭代过程中主要由两部分组成，第1部分是局部搜索阶段，该阶段的复杂度为O(3nk+mn).第2部分为交叉操作阶段，其时间复杂度为O(10n).因此本文算法的时间复杂度为O((3k+m+10)n).

4 实验分析

为了测试本文算法的性能，对一组小规模的实例和两组标准的数据进行了测验.第一组小规模的数据来源于文献[1].这组数据总共包含3个实例，规模最小的实例的工件数是3，机器数是3，总工序数为15.规模最大的实例的工件数是5，机器数是4，总工序数为20.本文程序采用MATLAB程序设计语言，在配置为core i7-4790 CPU@3.60 GHz 3.60 GHz和8 GB RAM的电脑上运行.在试验中蜜源与观察蜂的个数设定为200，控制次数limit为5，最大迭代次数为100.每次迭代过程中进行10次交叉操作.对每个实例独立运行20次.本文算法求出的结果与文献[1]中的混合多元优化(hybrid multi-verse optimization，HMVO)算法的结果对比如表3所示.表3中的基于邻域搜索的人工蜂群算法(artificial bee colony algorithm neighborhood search，ABCNS)对应的是本文算法，表中列出了两个算法所求出的最优结果、平均结果、最差结果.由表3的结果可知，本文算法和HMVO算法一样总是能找到最优结果，且平均结果和最差结果都与最优结果相同，说明了算法的稳定性较好.

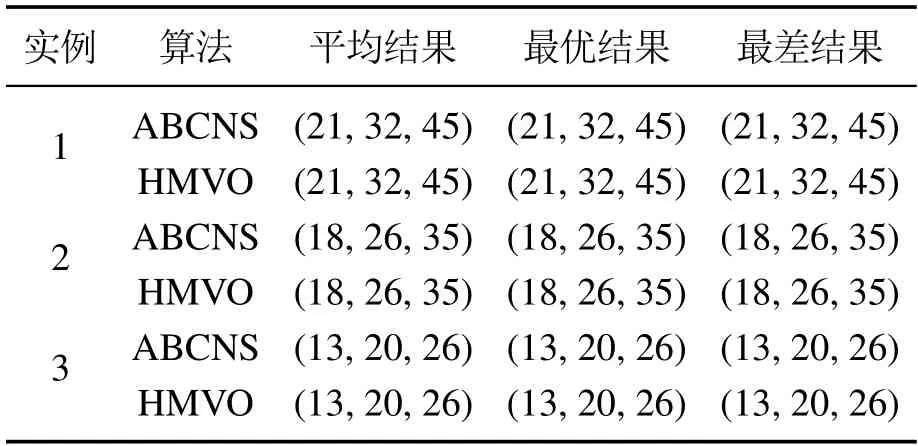
表3 小规模数据比较Table 3 Small-scale data comparison

第2组数据来源于文献[17-18]，这组数据总共有5个实例，规模最小的实例的工件数是10，机器数是10，总工序数为40.规模最大的实例的工件数是15，机器数是10，总工序数为80.这5个实例都是完全模糊柔性作业车间调度，各工序在所有机器上都可以进行加工.

为了验证本文算法的有效性，本文算法的结果与其他已经发表的文献中的7个算法的结果进行了对比.这些算法包括文献[1]中的HMVO算法、文献[29]中的IABC算法、文献[22]中的IDPSO算法、文献[21]中的DHS算法、文献[35]中的教学优化算法(teaching learning based optimization，TLBO)、文献[20]中的EDA算法、文献[28]中的HABC算法.在这些算法中，设定的种群规模都不一样.HMVO算法和TLBO算法的种群大小为200，IABC算法、DHS算法和EDA算法的种群大小为150，IDPSO和HABC算法的种群大小只有100.本文算法的种群大小与HMVO算法一致，设定为200.控制次数(limit)为5，每次迭代过程中进行10次交叉操作.对每个实例独立运行20次.虽然本文的种群大小比一些算法要大，但是本文算法的进化代数只有100代，也就是总共需要运行20000次，比HMVO算法的100000次要小的多.

表4中列出了各算法的平均结果，最优结果以及最差结果.表中的标黑字体表示的是所对比算法中求得的最好结果，由表中的结果可知，本文算法运行第1个实例的结果要优于其他的算法，虽然本文算法相对于第1个实例的最优结果与HMVO算法的最优结果相等，但是本文算法的平均结果与最差结果都与最优结果相等，说明了本文算法的稳定性比HMVO算法的要好.对于第2个实例，本文算法的结果与HMVO算法的结果都一样，优于其他算法的结果.对于剩下的3个实例，本文算法的结果都优于这些算法.图3给出了实例4的最优调度结果的甘特图.

为了验证本文算法中各部分对试验结果的影响，针对第2组标准数据集，做了3组分离试验.分离试验的结果如表5所示.表5中算法ABCNS(1)表示的是采用随机初始化所得的结果，由表中结果可知随着总工序数的增加，采用混沌初始化的优势更加明显.算法ABCNS(2)对应的是不采用交叉操作后所得的结果，由结果可知采用交叉操作后，平均结果、最优结果、最差结果都有所改善，体现了采用交叉操作的优越性.为了验证采用领域搜索的效果，将本文算法与传统的ABC算法的结果进行了对比.结果显示本文算法的结果明显优于传统的ABC算法.

第3组数据来源于文献[21]，这组数据总共有8个实例，规模最小的实例的工件数是5，机器数是4，总工序数为23.规模最大的实例的工件数是20，机器数是15，总工序数为355.这组数据是部分模糊柔性作业车间调度，有些工序只能在部分机器上进行加工.对于这组数据，本文算法与文献[1]中的HMVO算法以及文献[36]中的4种启发式方法进行了对比.这4种方法包括局部最小加工时间原则(LS)、全局最小加工时间原则(GS)、剩余工件最多原则(MReW)和随机原则(Random).在试验时，本文算法的蜜源与观察蜂的个数设定为200，控制次数limit为5，最大迭代次数为100.每次迭代过程中进行10次交叉操作对于前4组数据，HMVO算法的种群大小设置为100，迭代次数为500.对于后4组数据，迭代次数设定为1000.5种启发式算法的种群大小设定为150，对于前4组数据，最大迭代次数设置为1000.对于后4 组数据，最大迭代次数为4000.而本文算法的种群大小设定为200，最大迭代次数设定为100，所以本文算法总的运行次数要远远小于与之对比的算法.

表4 各种算法对第2组数据的计算结果Table 4 Computational results of various algorithms on the second data set

图3 第2组数据中实例4的最优结果甘特图Fig.3 Gantt chart of optimal results for example 4 in the second set of data

表5 分离试验结果Table 5 Separation test results

表6中列出了各算法相对于各个实例的平均结果、最优结果和最差结果.由表中结果可知，对于所有的实例，本文算法与HMVO算法的结果都要远远优于其他5种算法的结果.对于前5个实例的结果，无论是最优结果，还是平均结果和最差结果，本文算法的结果都比HMVO算法的结果好.尤其对于第1个和第2个实例，本文算法求得的最优结果、平均结果以及最差结果都相等，说明了本文算法的稳定性较好.但是对于第6个实例和第8个实例，本文算法求得的结果只有平均结果和最差结果优于HMVO算法，达不到HMVO算法求得的最优结果，但是与HMVO求得的最优结果的差距不大.对于第7个实例，本文算法的平均结果、最优结果和最差结果都比HMVO算法的差.原因可能是对于像实例6-8这些大规模的实例，本文算法易陷入局部最优.

图4展示了第3组数据中4个实例的进化曲线，分别为第1个实例、第3个实例、第5个实例和第8个实例.第1个实例的进化曲线是一条直线，说明在种群初始化完成后就可以达到最优结果，体现了采用混沌初始化的优越性.第3个实例的进化曲线在30代左右的时候达到最优，第5个实例的结果在40代左右的时候收敛到最优结果，第8个实例在40代左右的时候也达到了较好的结果，在70代左右的时候达到最优，而与之比较的HMVO算法要进化900次左右才能达到最优结果，所以本文算法在求解FFJSP时，具有很好的收敛性.

表6 各种算法对第3组数据的计算结果Table 6 Computational results of various algorithms on the third data set

图4 第3组数据中4个实例的进化曲线Fig.4 Evolving processes of four instances in third data set

5 结论

本文提出了一种基于NS的ABC来求解FFJSP，它以最小化最大模糊完工时间为优化目标.为了测试本文算法的性能，对3组标准数据集进行了测验，并将结果与一些文献中算法的结果进行了对比.结果表明，对于大部分的数据实例，本文算法所求出的结果都要优于与之对比的算法.为了直观地反映最优的调度方案，将第2组数据中的第4个实例的最优结果通过甘特图的形式展示了出来.并通过4幅种群的进化曲线图来反映算法的收敛情况.后期会将一些机器学习的经典算法与群智能算法相结合来求解多目标柔性作业车间调度问题.