大型风机主导机械动态的智能灰箱建模及其线性状态空间表征

潘晨阳，胡 阳，奚芸华

(华北电力大学控制与计算机工程学院，北京 102206)

1 引言

随着环境污染、能源短缺问题的出现和恶化，利用新能源的发电技术得到了人们的重视并成为研究的重点，因此，新能源发电实现了规模化的开发和发展.其中，风力发电因其清洁、资源丰富等突出优点获得广泛应用，近十年来，风电装机容量得以快速增长[1].在众多类型的风机中，大容量变速变桨风机具有度电成本低、多自由度灵活控制等优势，因而日益成为风电市场的主流机型.

现代风机具有本质非线性的特点，会受到复杂的外部环境干扰，且面临多重控制任务，因此，风机控制对于机组的安全高效运行具有至关重要的意义[2-4].然而，先进控制策略及控制算法的实施均高度依赖于风机的模型建立.其中，文献[5]重点研究了风机气动系统静态非线性的参数可辨识性，依据八独立参数模型进行辨识，模型结构比较复杂且具有高度非线性.文献[6-8]采用子空间辨识进行闭环条件下的风机系统辨识，但需要设计合理的辨识实验且重构的状态空间模型缺乏物理意义.文献[9-10]均利用神经网络进行风机系统的建模，此类方法易出现过拟合问题且模型可解释性差.文献[11]研究了传动系统和发电机的联合辨识问题，然而，传动系统仅采用单质块模型，模型复杂度可能较低，使其难以模拟较复杂的实际系统动态;此外，一般情况下，发电机参数单独辨识即可.文献[12-13]研究了定速风机双质块模型、三质块模型的智能参数辨识.然而，两者均未考虑多入多出条件下传动系统的辨识问题并以此来对系统进行建模，同时，尚未制定系统性的智能辨识步骤.经文献查阅，发现还未有研究提出风机主导机械动态的完全建模方法和求取其完整的状态空间表述，采用线性分段仿射(piece-wise affine，PWA)结构表征气动系统的静态非线性，与传动系统的线性状态空间模型联合，可有效构建风电机组主导机理动态的高精度线性状态空间模型;区别于基于Jacobian线性化的局部线性动态表征特性，线性PWA模型具有区域动态表征能力.在此基础上，可以实现风电机组在全风速工况下非线性动态的高精度线性状态空间表征.本文基于机组的运行数据构建符合机理原理且适用于工程应用与研究的风机机械系统状态空间模型，将有利于风机的控制设计和分析，能适用于智能控制研究[14-16]中，取代由理论设计参数值构建的模型，可为其奠定重要的模型基础，也可用于风机状态监测、故障诊断及预警等应用中，因此对于风机的研究而言具有必要性和重要性.

综上，本文基于风机主导机理模型特性分析，首先建立了气动转矩的PWA模型来描述气动系统的静态非线性.然后，设定了加权归一化的综合误差准则，并系统地提出了智能灰箱参数辨识步骤，将其应用于多入多出传动系统建模中获取状态空间模型.将分别求解的气动系统和传动系统模型对接，构建出适用于控制设计的完整简化模型，用于表征主导机械动态.最后，基于FAST中5 MW风机模型进行仿真验证和对比分析，以检验所提方法的有效性和联合模型的性能.

2 风机子系统

2.1 气动系统

风机气动系统用于将捕获的风能转化为机械能，根据空气动力学原理，风轮实际捕获功率为

式中:ρ为空气密度;R为风轮半径;V 为叶片来流风速;CP为风能利用系数，反映静态气动特性，一般表示为叶尖速比λ和桨距角β的非线性函数形式:

其中:叶尖速比λ的定义为λ=Rωr/V，ωr为风轮转子转速.忽略风机损耗功率，则风机气动转矩为

式中 CT(λ，β)=CP(λ，β)/λ[17]为转矩系数.风轮对塔架的前后向推力为

式中:CF(λ，β)为推力系数，CF(λ，β)=CP(λ，β)/λ[17].需注意此处的转矩和推力系数的表达式仅适用于忽略损耗功率的情形.

FAST采用叶素动量理论进行详细的气动系统建模，利用WT Perf软件可导出其静态非线性.

2.2 传动系统

风机传动系统的主要组成部分有风轮转子、低速轴、齿轮箱、高速轴和发电机转子.风轮的机械能先传递给齿轮箱的低速轴，再经由齿轮箱变速作用最终由高速轴传递给发电机部分.

传动系统的主流建模方法为等效质量集中法，其常用的近似模型主要分为3 种，分别是单质块[18]、双质块[19]、三质块模型[20-21].其中，双质块模型足以反映系统机械动态并常用于控制设计，它假设高速轴为刚性轴，同时考虑低速轴的柔性和阻尼特性，其示意图如图1所示.经过质量等效，建立双质块数学模型如下:

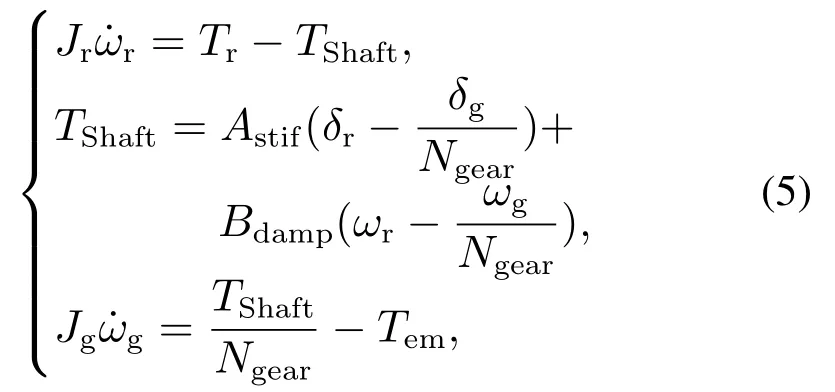
式中:Tr和Tem分别为气动转矩和发电机电磁转矩;ωr和ωg为风轮转子转速和发电机转子转速;TShaft为等效中间轴转矩;Jr和Jg为风轮转子和发电机转子的转动惯量;δr和δg为风轮转子侧和发电机转子侧的角位移，且有为齿轮箱变速比;Astif，Bdamp为等效的中间轴刚度系数和阻尼系数.

图1 双质块模型Fig.1 Two-mass model

根据双质块数学模型，以Tr和Tem作为系统输入、ωr和TShaft作为输出，得到状态空间模型如下:

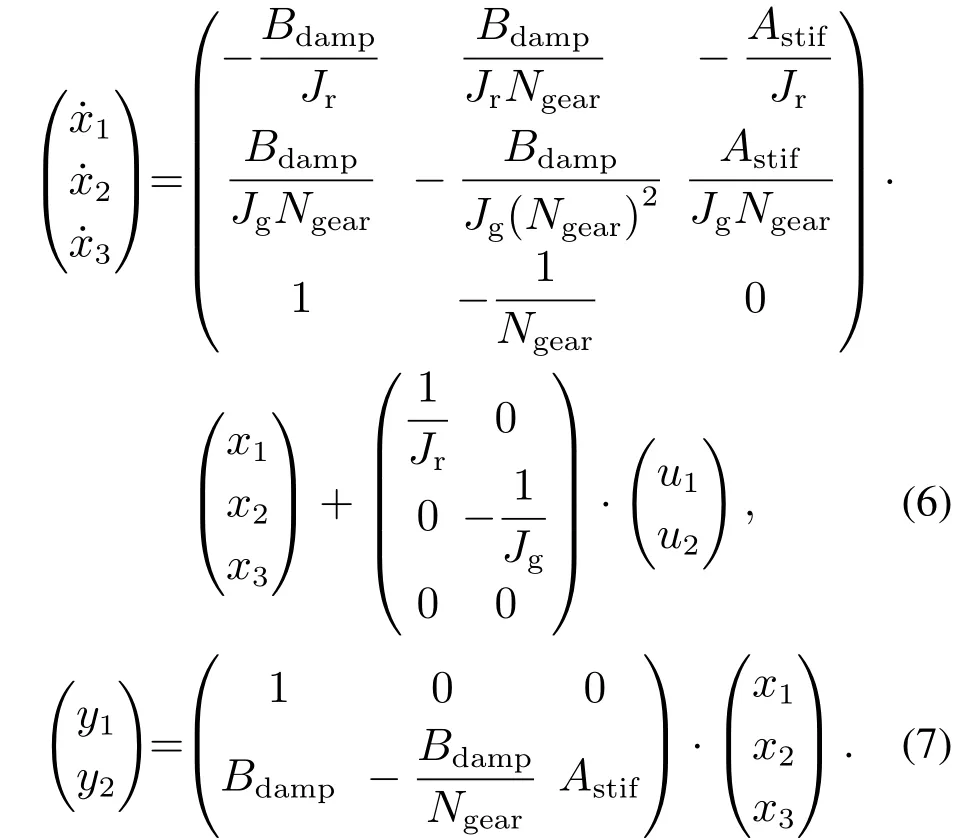
其中:式(6)为状态方程，式(7)为输出方程:

将状态空间模型转换为输入输出间传递函数如下:

式中:

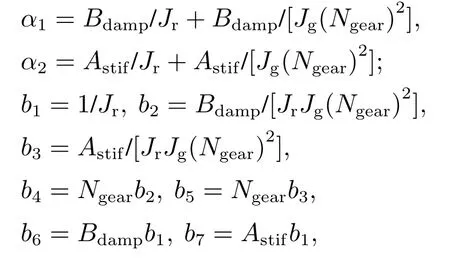
由式(8)可知，输入到输出ωr间的传递函数均包含一个积分环节，说明其无自平衡特性，而输入到输出TShaft间的传递函数都包含同为0的零、极点，因而发生零极点对消，传递函数中不存在积分环节，这表明其有自平衡能力.

如图2所示，在阶跃扰动下，无自平衡能力对象无法在不依赖外界调节作用的条件下达到一个新平衡状态，而有自平衡能力对象可以靠自身达到新的平衡.

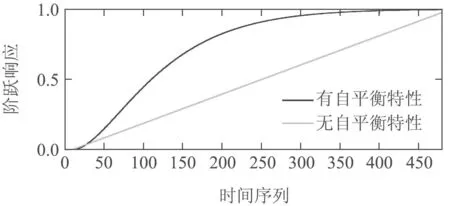
图2 阶跃响应特性Fig.2 Step response characteristics

3 气动转矩的PWA建模

风机的气动转矩是气动系统的输出，由式(3)可知，气动转矩是关于ωr，β，V 的非线性函数，这种非线性关系很难用一个适用于全局范围的、简单的单一模型进行描述，在此采用PWA模型来拟合气动转矩，划分不同运行区域利用线性模型近似其静态非线性特性.PWA模型是一种具有特殊模型结构的多模型方法，它包含有限多个局部子模型，可依据切换律在不同子模型间进行转换，同时每个子模型都具有简单的形式.PWA模型有多种结构形式，考虑此处的建模问题，可采用如下结构的PWA模型:

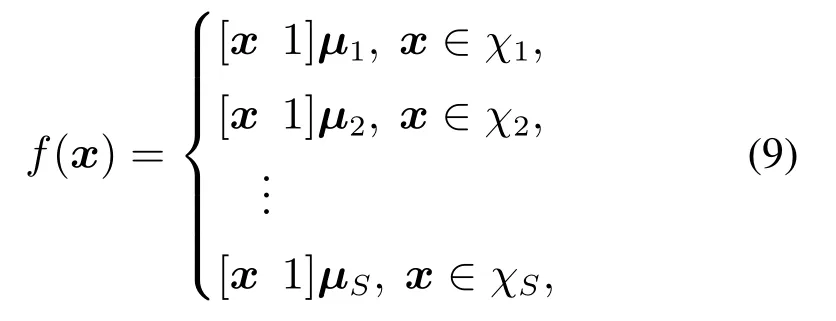
其中:x代表模型的输入，x∈R1×n;μi，χi分别是第i个子模型的参数向量和作用域;S代表子模型数量.

由前面的分析可知，气动转矩的PWA 建模中，模型输出Yk=Tr(k)，模型输入xk=[ωr(k) β(k)V(k)]，需要计算出模型参数并在ωr-β-V 三维空间中得到各子模型的作用域.建立气动转矩的PWA模型可分解成如下步骤:

1) 建模数据的聚类划分.原始建模数据需要划分为S个数据簇分别作为各局部子模型的建模数据.在此，不采取直接对原始数据聚类的方式，而是兼顾数据点的空间特性以及各数据点参数向量间的相似性构造和计算基于原始数据的特征向量，对特征向量进行聚类操作实现对其对应原始数据的聚类[22].

首先，分别以每个数据点(xk，Yk)为数据中心建立局部数据集，每个局部数据集Ck包含c个数据点，即数据中心和其邻近的c-1个数据点.其中，邻近的数据点是根据各点的模型输入向量xj=[ωr(j) β(j)V(j)](j/=k)与数据中心的模型输入向量xk=[ωr(k) β(k) V(k)]之间的欧式距离选出的距离最小的c-1个点.基于Ck中数据利用最小二乘计算公式求取数据集Ck的参数向量PVk，结合Ck中数据点模型输入向量xj=[ωr(j) β(j) V(j)]((xj，Yj)∈Ck)的均值Mk共同构成特征向量FVk=[(PVk)TMk]T.

然后，计算PVk的经验协方差矩阵Vk[23]，并针对Ck中数据点的模型输入向量计算用于度量类内离散度的散度矩阵Qk[24]如下:

将特征向量视为均值为FVk且服从高斯分布的随机向量，则特征向量的协方差可估计为Rk=[Vk0;0 Qk].依据高斯分布特性，将特征向量取值为均值FVk的置信度用ωk来衡量，ωk可赋值为

选取K-means算法[25]对特征向量聚类，考虑到特征向量计算结果可能会包含一些异常值，将引入到聚类目标函数和聚类中心更新的计算中作为距离测度使用[22]，实现将特征向量数据分成S个数据簇，与其对应的原始数据也就划分成S组，将划分好的S组原始数据分别记作D1，D2，…，DS.

2) 子模型参数辨识.将经数据聚类获得的S组数据分别用作S个局部子模型的辨识数据，以ωk作为数据点(xk，Yk))的权重应用加权最小二乘法辨识各子模型参数μi，即μi能满足式(12)达到最小化的条件.

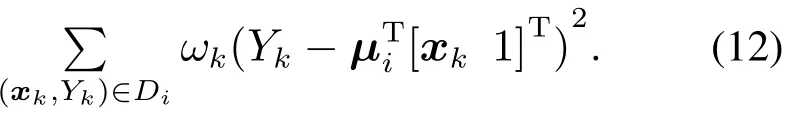
3) 子模型作用域估计.各局部子模型作用域求解可转化为求取数据簇间划分超平面，本文借助常用于分类的支持向量机获取切换面方程的系数，由于每类数据之间不一定完全线性可分，因此采用鲁棒性和泛化能力更好的软间隔支持向量机[26]，算法的优化目标为

式中:φ和d分别为切换面的法向量和偏移量;ξk为松弛变量，反映了数据不满足硬间隔约束yk(φTxk+d)≥1的程度;γ 表示惩罚系数，可根据结果调整该系数;yk是数据的分类标签，有1和-1两种取值，可定义为yk(xk)=sgn(φTxk+d);m为用于分类的数据总数量.

根据聚类结果应用上述软间隔支持向量机可在ωr-β-V 三维空间中求解出相邻类之间的分割平面方程，从而与其它分界面共同构成各子模型的作用域.

4 风机传动系统智能灰箱辨识

4.1 智能灰箱参数辨识步骤

粒子群优化[27](particle swarm optimization，PSO)算法是受鸟群觅食行为启发而诞生的一种模拟生物活动的进化计算方法，该算法的收敛速度快，能够较好地解决非线性、多峰值等复杂的优化问题.

将PSO算法应用于参数辨识的流程框图如图3所示.

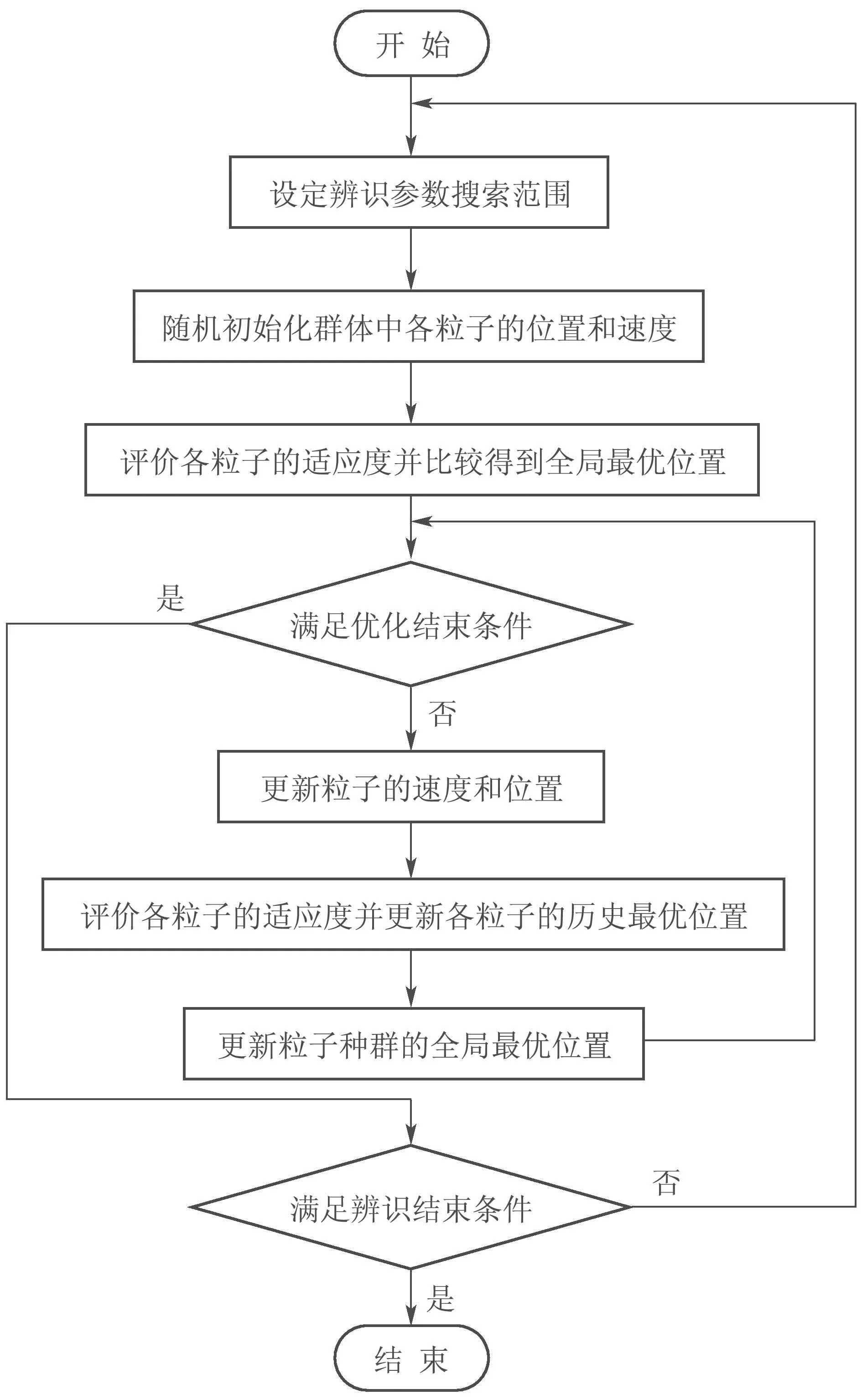
图3 智能辨识流程框图Fig.3 Flow chart of intelligent identification

具体步骤如下:

1) 确定参数搜索空间.采用PSO算法时需先给定初始的参数搜索范围来构建解空间，在参数参考值已知的情况下，可以此为参数搜索区间中心预先设定一个较宽泛的区间，例如参考值的[-35%，+35%]区间.若参考值未知，可根据经验知识结合其他准确性不太高的辨识结果设定参数范围.

2) 辨识参数寻优.在确定好参数范围的前提下，给定算法参数以及定义适应度函数，然后利用PSO算法求解辨识参数.其中，在速度的更新规则中引入动态惯性权重，以线性递减权值策略作为惯性权重的动态变化规则，用于调整和平衡粒子搜索时的开发(exploitation)能力和探索(exploration)能力.当进化代数达到设置的最大值时，优化过程结束.

本文采用的PSO算法中，结合动态惯性权重的粒子速度更新以及位置更新公式如下:

式中:ϖ为惯性权重;c1，c2为加速度因子，此处都取1.5;rand1，rand2为相互独立的、介于[0，1]的随机数.分别为进化到第k+1代时第i个粒子的速度和位置;pbesti和gbest分别为第i个粒子个体的最优位置、整个种群的最优位置.需要注意的是，速度和位置的更新过程中如果超出设定范围，需对其加以限制，以约束在设定范围内.

其中，进化到第k代时的惯性权重由下式计算:

式中:Gmax为最大进化代数，ϖini为初始惯性权重，ϖend为进化到Gmax代时的惯性权重.在此，取典型值ϖini=0.9，ϖend=0.4.

3) 调整参数搜索空间.依据算法辨识结果收缩参数搜索区间，再次执行2)的操作.

重复循环2)-3)步骤以不断逼近最优值，直至算法得到收敛的结果或者达到期望的精度，此时优化算法计算出的种群最优位置即为辨识参数的解.

4.2 参数辨识优化问题描述

借助PSO算法辨识系统时除了确定算法各参数，建立用于评价的适应度函数也是算法的核心.辨识问题中，适应度函数等同于系统辨识的目标函数，系统辨识本质上也是优化问题，构建其优化目标函数需要依据一定的辨识准则.辨识准则是用来评价与衡量辨识模型与实际系统接近程度的标准.其中，误差准则是最常用的辨识准则，误差可具化为输出误差、输入误差或者广义误差等，在此可考虑基于最小化输出误差建立优化目标函数.

对于传动系统，可选择其辨识输入为Tr和Tem，大多数研究中仅考虑将转子转速作为辨识输出，为了更好地拟合系统动态，在此选定辨识输出为ωr和TShaft，综合考量这两个输出的误差，构造加权单目标函数.为了避免输出变量间数量级差异的影响，有必要先对每项输出误差标幺化处理再加权得到综合误差，则构造辨识目标函数为

式中:ζj是第j个输出的误差在目标函数中的权值，对于输出ωr和TShaft，均设权值为0.5;yj，st表示第j个输出的额定值或最大值(额定值未知或不存在的情形).

根据辨识结果所得的传动系统模型可直接与气动系统的PWA模型结合，构成联合状态空间模型描述风机主导机械动态特性.

5 仿真验证

为了保证数据的均衡性并且较好地提取出系统的静态特性，首先，以10分钟内的平均风速为依据，将全风速区间划分为若干风速区间段;在各个区间段内利用TurbSim生成含湍流风的实际风速.然后，在全风速区间内(包含额定风速以上、以下风速区域)较为均匀地选取整体呈递增趋势、波动不剧烈的风速数据点，即针对含湍流风的风速数据，按风速区间段大小依次均匀截取风速数据，进行组合并覆盖全风速区间.最终，以组合后包含8300个数据点的数据序列作为风速输入数据，如图4所示.利用FAST中5 MW风机模型生成数据来表征气动系统的完整特性，得到8300组ωr，β，V 数据和其对应Tr数据作为建模数据.实际情况下，Tr一般不可测量，可根据式(3)由气动功率除以ωr近似计算的Tr作为模型输出，在此直接利用软件导出的模型仿真输出.由于风机依据风速情况在两种控制策略间切换，同时考虑到在额定风速附近的过渡区域存在波动性和不确定性，选择将建模数据先根据β是否为零划分为两部分数据集，再分别进行聚类和模型估计，最终合并为气动系统全局模型.

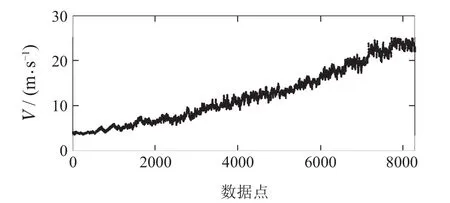
图4 输入风情况Fig.4 Input wind condition

为了合理地选择聚类的参数，引入DB指标[28]作为聚类效果的评判指标，综合考虑聚类结果的类内紧致性和类间分散性，其定义如下:

其中:diam(Li)为数据簇Li中各点到簇中心的平均距离，用于度量Li中样本间的紧密程度;d(Li，Lj)可根据Li与Lj的簇中心之间的距离得出，是不同簇样本间分散程度的一种测度.由指标定义知，类内越紧致，类间越分散，DB指标越小，表示聚类效果越好.选择不同的c和S进行聚类，计算其DB指标，结合数据聚类情况的变化，对于β为零的数据集，设定S=3，c=85，计算时对这部分数据集的特征向量空间做降维处理;对于β非零的数据集，设定S=4，c=80.利用数据特征向量聚类对应得到ωr-β-V 空间中数据的完整聚类结果如图5所示，其中7种颜色分别标记聚类分成的7类数据簇.

图5 ωr-β-V 空间中数据聚类结果Fig.5 Clustering results of data in ωr-β-V space

对相邻数据集两两应用软间隔SVM得到各类间分割超平面如图6所示，再利用各子模型数据集分别以加权最小二乘法估计模型参数，求得PWA模型如下:

式中:u(k)=[x(k) 1]，x(k)=[ωr(k) β(k) V(k)].完整的作用域表示还包括基于物理限制构建的平面，在此，仅以核心的分割平面作为代表，简化描述PWA模型的作用域.

将建模所用数据代入上述PWA模型验证其对建模数据的拟合效果如图7所示.根据图中的误差可知，求取的模型对大多数工况的建模精度都较高.

为了进一步检验和分析PWA模型的性能，选择适用于解决非线性回归问题的极限学习机(extreme learning machine，ELM)[29]方法对气动转矩进行建模，设置隐含层神经元的个数为30、激活函数为“sig”类型，得到结果如图8所示.

对比图7-8可知，ELM模型和PWA模型都取得了较好的拟合效果，两种模型的精确度比较相近.为了量化误差进行比较，计算两种方法下估计值与实际值之间的均方根误差，得到采用PWA，ELM的误差分别为9.9951×104和9.9846×104.此处求得的PWA 模型作为近似的分段线性模型，与ELM模型相比模型估计误差相近，并且结构更为简单.采用PWA模型进行气动转矩的建模可以在保证一定拟合精度的条件下与传动系统状态空间模型进行合并得到风机主导机械动态整体的线性表征.

对于传动系统辨识，为了探索无激励实验可辨识性，随机地设置了两个不同湍流强度的激励风场景:场景1(湍流强度为0.15)、场景2(湍流强度为0.135).输入风时长均为20 min，各场景输入风情况如图9(a)-(b)所示.

图6 类间分割平面Fig.6 Partition planes between classes

图7 PWA模型的估计结果Fig.7 Estimation results of PWA model

图8 ELM方法的估计结果Fig.8 Estimation results of ELM method

图9 各场景的输入风Fig.9 Input wind of each scene

仿真采用FAST软件的5 MW风机模型，5 MW风机的切入、额定、切出风速分别为3 m/s，11.4 m/s，25 m/s，风轮半径为63 m，额定风轮转子转速、发电机转子转速为12.1 r/min，1173.7 r/min，齿轮箱变速比为97:1.可由模型根据各场景输入风仿真生成传动系统各输入、输出数据作为辨识数据集，选取采样周期为0.05 s.利用基于PSO的智能辨识方法进行辨识，其中，选取PSO的种群规模和最大进化代数为50，150，得到各场景下参数辨识结果如表1所示，由此计算辨识参数相对误差如表2所示.

表1 传动系统参数辨识结果Table 1 Parameter identification results of drive-train system

表2 辨识参数的误差Table 2 Errors of identified parameters

PSO辨识过程中最后的适应度进化情况如图10所示，两种场景下适应度进化都在50代左右达到了收敛状态.

结合表1、表2中的结果对比各场景下辨识值，可知不同场景下对于两个转动惯量参数的辨识精度都很高，刚度系数和阻尼系数的辨识精度相对低一些，但也都在±25%的范围内，可见，在参数辨识准确度上PSO取得了较好的效果.

将PSO辨识的参数代入传动系统含参数的状态空间模型中得到系统模型，与求解出的气动模型(19)合并即为两者的联合状态空间模型.在此利用构建的气动转矩模型估计Tr，以此为输入导入传动系统模型中估计下一时刻输出，传动系统的风轮转子转速又将传递给气动转矩模型.在不同场景下检验联合模型的性能，将其估计的系统动态与风机模型直接导出的输出动态进行对比.计算各情形下系统估计输出如图11-12所示.

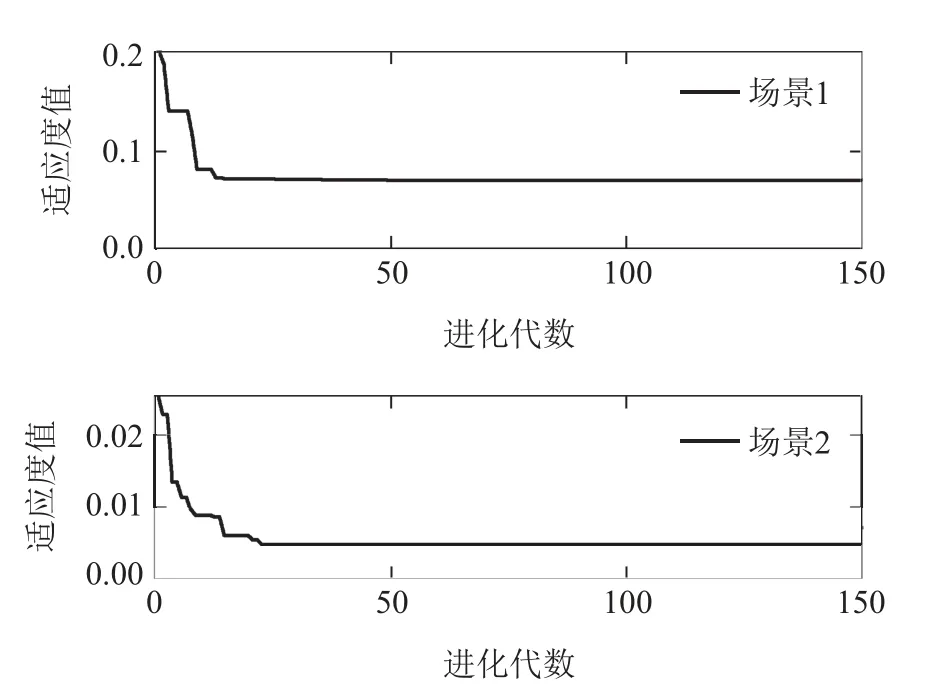
图10 适应度进化曲线Fig.10 Fitness evolution curve

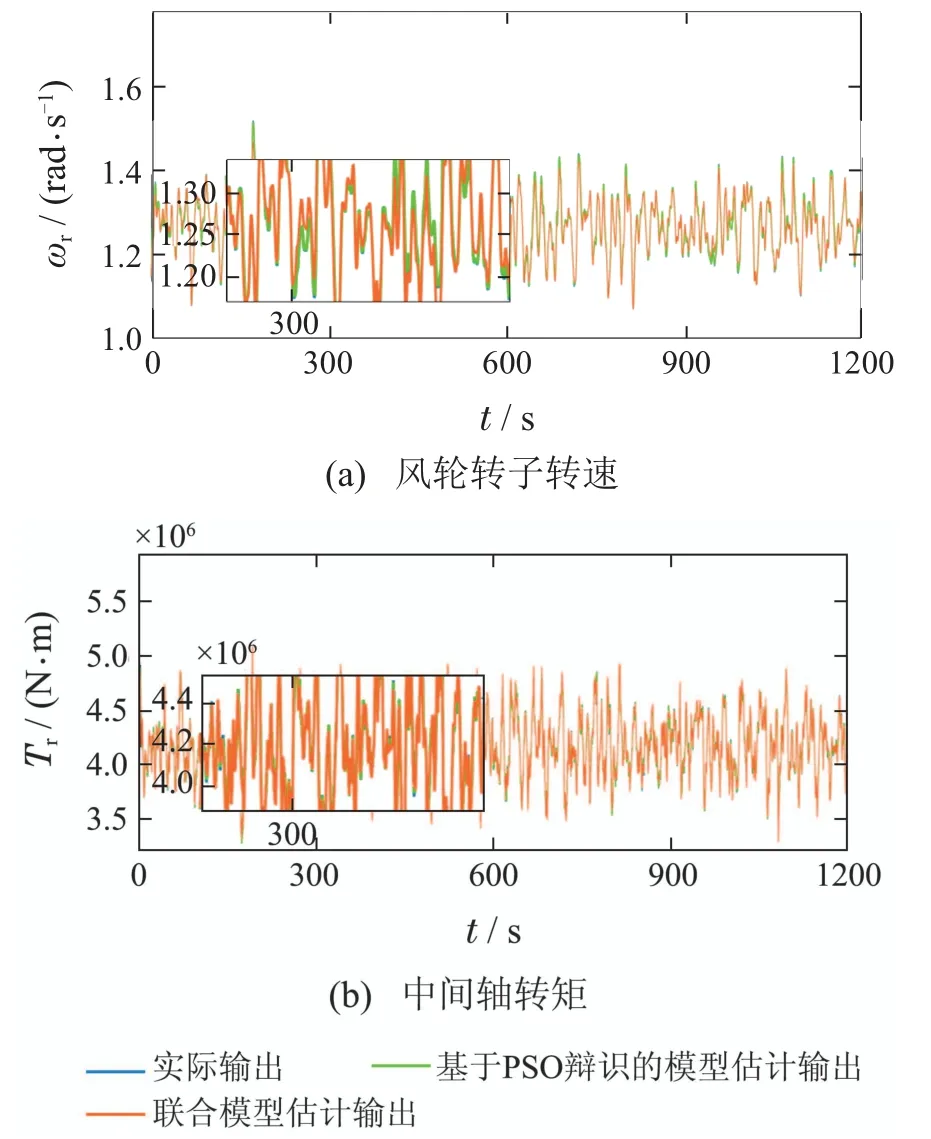
图11 场景1的输出估计Fig.11 Output estimation of Scene 1

图12 场景2的输出估计Fig.12 Output estimation of Scene 2

从图11和12中可知，利用辨识参数构建的模型在设定的两种场景之下的输出都能很好地跟随实际的传动系统输出，即对实际系统输出的动态特性拟合程度很高，并且图11和图12也显示出联合模型在两场景下的动态特性均较接近实际特性，可利用量化指标进一步验证.为了便于对比输出估计效果，采用均方根误差量化估计误差.计算各情形下估计输出与测量输出间的均方根误差如表3所示.

表3 估计输出的误差Table 3 Errors of estimated outputs

利用估计误差更小的场景2中PSO参数辨识结果计算传动系统传递函数模型的零极点:

1) Tr到ωr间传递函数W11:极点为0，-0.6276±13.3413i;零点为-0.5539±12.5353i;

2) Tem到ωr间传递函数W12:极点为0，-0.6276±13.3413i;零点为-142.1080;

3) Tr到TShaft间传递函数W21:极点为0，-0.6276±13.3413i;零点为0，-142.1080;

4) Tem到TShaft间传递函数W22:极点为0，-0.6276±13.3413i;零点为0，-142.1080.由零极点计算结果得到传动系统零极点分布如图13所示.

由计算结果和分布图可知，W21，W22有完全相同的零极点，且都在原点处存在零极点对消，其余的零极点均位于左半平面，所以从输入到输出TShaft间的系统有自平衡能力.W11和W12都包含原点处的极点，除此之外的零极点也都位于左半平面，因此从输入到输出ωr间的系统是无自平衡能力的.综上，上述计算结果的分析与前面的机理分析一致.

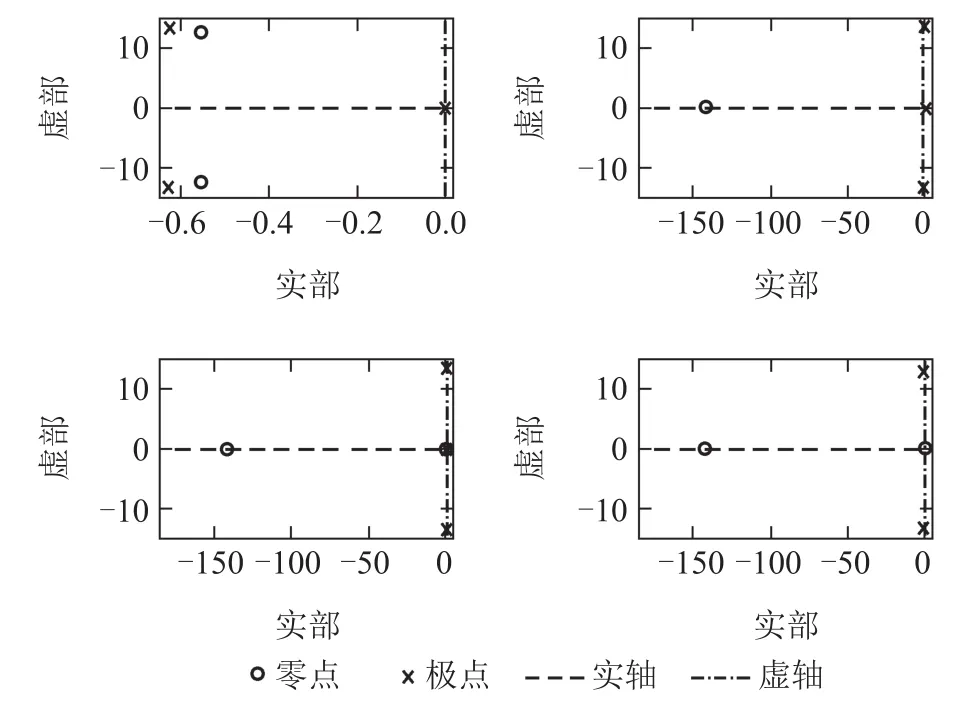
图13 传动系统零极点分布Fig.13 Zero-pole distribution of drive-train system

结合两场景下的参数辨识情况，可知PSO对参数的辨识一致性较强，即不同情形下的辨识结果没有出现巨大的差异，并且辨识参数有较高的准确性，通常情况下能取得对系统动态良好的拟合效果，故从整体来看，智能辨识有着稳定的性能.选取智能灰箱辨识方法作为传动模型的求解方式，从表3中可知，采用该方法辨识出的传动模型与气动模型共同构建的完整联合状态空间模型估计的系统输出与实际输出间的误差较小，模型动态与系统实际动态间差异度小，说明了所得联合模型的有效性.

综上，基于仿真数据求解的气动转矩PWA模型经建模数据集检验具有较高准确度，传动系统辨识结果表明了智能灰箱参数辨识方法的有效性，对于不同的辨识数据，它展现出稳定的辨识性能.智能辨识既能有效逼近系统动态，同时兼顾参数的物理意义和取值范围，因此本文采用该辨识方法完成传动系统建模，与气动系统PWA模型结合得到的联合模型也展现出较好的性能，可用于对实际系统的简化，作为后续控制工作的基础.

6 结论

基于风机机械系统的主导机理模型，解析了子系统特性.建立气动转矩PWA模型近似估计实际Tr，代表气动系统特性.考虑传动系统的两个输出ωr和TShaft，构建了加权形式的辨识优化目标函数，提出了一套系统的风机智能灰箱参数辨识方法，基于FAST的5 MW风机模型进行仿真，结果验证了智能灰箱参数辨识的有效性以及准确性.根据两个子系统模型的单独辨识结果，进行模型的合并得到联合模型，将模型动态与实际系统动态对比，结果验证了联合模型的准确性.整个建模过程可类比于实际风机的建模，在后续的研究工作中，拟采用实际风机的运行数据，对本文提出的建模策略的有效性进行进一步论证，获取实际风机主导机械动态的线性状态空间表征.此外，静态模型仅具有有限的动态表征能力，可能需要进行动态补偿，以准确逼近风机的非线性动态，这也是后续研究的重点问题.