高炉煤气流分布过程的多算法融合预测模型

吴晓阳，张 森，陈先中，尹怡欣

(北京科技大学自动化学院，北京 100083;北京科技大学工业过程知识自动化教育部重点实验室，北京 100083)

1 引言

钢铁工业是国民经济的支柱性产业.高炉是钢铁生产过程中的核心设备，关系到钢铁行业的工业产量和能源消耗.维持高炉的稳定顺行是整个钢铁行业共同追求的重要目标[1].在高炉生产中，炉顶的煤气流分布直接反映了煤气热能的利用情况，因而影响高炉能耗水平和生产成本，所以准确的预测高炉煤气流分布状况将有助于保证高炉的稳定顺行[2].然而，高炉在运行过程中处于“黑箱”状态，使得高炉操作人员无法直接观测煤气流的分布及其状态变化.因此关于高炉煤气流分布状况的预测一直是学术界和工业界的热门研究方向[3].高炉煤气流分布的预测有利于研究高炉料面的变化规律，从而指导布料操作.随着检测技术的发展，包括红外成像、十字测温等先进技术较为成熟的运用在高炉煤气流的实时检测中，使得煤气流的预测成为了可能.Li等人[4]基于小波概率神经网络建立一种煤气流分布辨识模型.Zhang 等人[5]建立了一种基于低频特征提取技术的支持向量回归模型预测高炉煤气流分布状况.Shi等人[6]提出了一种基于红外图像处理的高炉煤气流中心分布特征识别方法，采用模糊C均值聚类和统计方法对高炉煤气流中心的分布特征和相应的气体利用率进行了分类.An等人[7]提出一种基于炉顶摄像检测的高炉炉喉煤气流形态三维模型重建方法.Zhou等人[8]基于时间序列思想，采用多输出自回归移动平均模型、主因子分析法、Pearson相关性分析、赤池信息准则与模型拟合优度等技术，提出一种结构简单、精度高且易于实现的十字测温中心温度在线估计方法.虽然上述模型均可实现对高炉煤气流分布状况的研究和预测，但是仍然存在两个问题使模型的准确性无法令人完全信服.

问题1在高炉运行过程中，基于十字测温装置和红外图像处理技术所得到的温度数据总是不同程度的带有异常数据.异常数据产生的原因，既有因高炉内部粉尘与高温煤气密布等环境因素产生的环境噪声，也有因长期处于高温高压环境下导致的测量仪器损坏所产生的测量误差，而后者的影响更为恶劣.使用滤波等数据预处理手段虽然可以有效去除环境噪声但是却无法完全排除测量误差.

问题2传统高炉煤气流温度预测模型主要集中在优化模型，提高预测精度上，而忽视了在工程中的实用性.大多数预测模型属于单步预测，虽然具有很高的精度，但是只能为高炉操作人员提供一分钟甚至几十秒的预测结果，而这对实际操作的帮助十分有限.

针对以上所提到的问题，本文基于真实的高炉十字测温数据，将带遗忘因子的递推最小二乘法的自回归移动平均模型(auto-regressive moving average model based on recursive least squares with forgetting factor，FF-ARMAX)和限定记忆的正则化极限学习机(regularized extreme learning machine based on recursive finite memory least squares，RFMLS-RELM)两种数据驱动算法融合建立高炉煤气流多步预测模型.首先，利用时间序列分析能够准确反映动态依存关系的特性和带遗忘因子的递推最小二乘法能够降低历史数据影响力的特性建立FF-ARMAX模型，通过该模型对十字测温装置产生的测量误差进行修正，并且运用傅里叶变换法去除内部环境产生的环境噪声，以减少原始数据与真实情况之间的差距，提高预测结果的可靠性.然后分别选取十字测温装置中的17个测温点作为输出变量，如图1所示，使用经过数据预处理的高炉数据，结合正则化极限学习机(regularized extreme learning machine，RELM)算法，建立高炉煤气流多步预测模型.考虑到传统的RELM算法会随着训练样本的不断增加，而逐渐失去学习能力，也就是新的样本无法对模型产生影响，即“数据饱和”问题，本文运用限定记忆递推最小二乘法(recursive finite memory least squares，RFMLS)优化RELM，从而保证模型的预测精度和可信度.实验结果表明，采用改进的RELM算法建立的高炉煤气流多步预测模型可以准确预测高炉煤气流分布状况，为高炉操作人员分析炉况提供了有效的帮助和支持.

图1 十字测温装置Fig.1 The crossing temperature device

2 煤气流分布影响因素分析及数据预处理

传统高炉煤气流分布预测模型中，模型输入变量的确定大多根据经验主观确定，容易造成模型特征冗余或关键特征丢失，影响预测精度和建模效率.因此，在建立高炉煤气流多步预测模型之前，首先需要确定影响高炉煤气流分布的相关影响因素作为预测模型的输入变量.同时，由于温度数据中存在由采集装置导致的测量误差和生产环境导致的高频噪声.因此需要对从高炉生产现场采集到的原始数据进行数据预处理，具体而言就是分别进行测量误差处理和数据去噪处理，使数据能够更加真实的反映高炉生产信息，从而提升预测模型的性能，提高预测精度.

2.1 煤气流分布影响因素分析

本文除采用十字测温装置的测温点作为影响因子外，还选择高炉炉况信息等其他影响高炉煤气流分布的相关因素作为影响因子，进行煤气流分布影响因素分析.由于本文需要对测温点进行预测，故选择十字测温装置的各测温点作为预测模型的输出变量.本文选取风量(FL)、风温(FW)、风压(FY)、顶压(DY)、富氧量(O2)、风速(FS)、压差(YC)和17个测温点，共计24 个变量作为影响因子.选取1000组高炉现场数据，相关影响因子的详细数据信息如表1所示.由于篇幅有限，此处以十字测温装置中的T25测温点为例进行影响因素分析.分析采用Pearson相关性分析，分别计算这23个影响因子与输出变量T25之间的相关程度.Pearson相关系数的计算公式如下:

式中:ai，bi表示第i时刻两个变量的采样值;表示变量均值;n为采样总量.

表1 高炉数据详细信息Table 1 Blast furnace data details

根据式(1)计算得到每个影响因子与输出变量T25的相关系数，结果如图2所示.

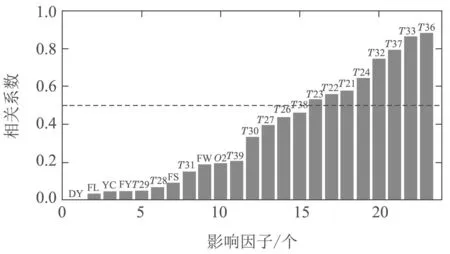
图2 影响因子与T25的相关系数Fig.2 The correlation coefficient between the influence factor and T25

为降低模型复杂度，需要进行数据降维，因此选取相关性大于r0=0.5的影响因子作为模型输入.如图2中所示，灰色虚线标识的地方即为r0=0.5处，本文选取Pearson相关系数大于0.5的影响因子作为输入变量.由此得到高炉煤气流多步预测模型以T25为输出变量所对应的输入变量为T23，T22，T21，T24，T32，T37，T33和T36.

2.2 数据预处理

由于信息采集装置的老化、失效等问题和高炉内部环境复杂多变，高炉生产现场采集到的数据不可避免存在着各种误差.有因信息采集装置所处的恶劣工作环境导致的仪器老化、损坏等问题而产生的测量误差，也有因高炉内部本身复杂多变的环境而产生的环境噪声.并且，使用存在着误差的高炉数据建立预测模型会使预测效果变差，所以需要先对高炉生产数据进行预处理.接下来数据预处理将会分为两个部分进行，一个建立FF-ARMAX模型修正测量误差，一个是通过傅里叶变换消除环境噪声.

2.2.1 基于FF-ARMAX的测量误差处理

十字测温装置的热电偶因为自身所处的恶劣环境，极易损坏，导致测量数据出现严重的测量误差，本文针对温度数据在时序上存在测量误差的问题，提出通过建立FF-ARMAX模型对测量误差进行修正的方法.时间序列分析的基本思想是根据观察到的历史数据，建立能够比较精确地反映时间序列中所包含动态依存关系的数学模型[9]，所以可以通过分析从高炉现场获取的输入输出时间序列数据之间与输出时间序列之间的相互关系来建立十字测温装置测量误差修正模型.时间序列分析中ARMAX模型的一般结构为

式中:

z-1为延迟算子，即z-1y(k)=y(k-1); ε(k)为零均值高斯白噪声;np，nq为滞后的阶次，k为采样时刻.

1) 变量选取.

建立FF-ARMAX模型是为了消除数据中存在的测量误差，因此需要先确定哪些变量数据中存在测量误差.由表1可知，变量T25和T29(字体加粗标明)的最小值均为-12.5℃，显然高炉中不可能出现零下温度，因此这两个变量必然存在测量误差，需要通过FF-ARMAX模型修正.此处以T25为例.选取T25作为输出变量，输入变量的选取采用第2.1节中的相关性分析方法，经过分析最终选取T23，T22，T21，T24，T32，T37，T33和T36作为输入变量.

2) 模型定阶.

建模过程中增加模型阶数可以提高模型精度，但是模型复杂度会增大，提高了建模难度，并易于导致过拟合问题.为此，采用信息准则作为确定模型阶数的依据，信息准则通过加入模型复杂度的惩罚项来避免过拟合的问题.最常用的信息准则为赤池信息准则(Akaike’s information，AIC)[10]:

式中:d为模型参数个数;v为损失函数;N为训练样本容量.本文采用MATLAB中的armax(·)函数和aic(·)函数进行模型定阶，确定式(2)-(3)中滞后阶次np，nq.滞后阶次的选取范围为np∈[1，5]，nq∈[1，5]，N=1000，实验结果如图3所示.

图3 (a) 模型AIC与不同输入输出阶次的三维立体图Fig.3 (a) The AIC value corresponding to different order(three-dimensional map)

图3 (b) 模型AIC与不同输入输出阶次的俯视图Fig.3 (b) The AIC value corresponding to different order(top view)

由图3(a)和图3(b)可以看出，当np=3，nq=3时，AIC函数值最高，因此模型阶次确定为np=3，nq=3.

3) 模型参数辨识.

由式(2)-(3)可知，需要建立的FF-ARMAX模型表达式为

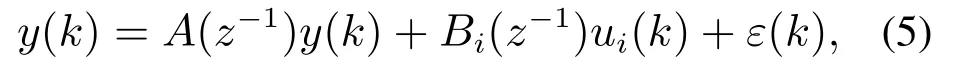
式中:

定义数据向量和参数向量:

其中i=1，2，…，NR，NR为输入变量个数.

将式(7)和式(8)代入式(5)，可得

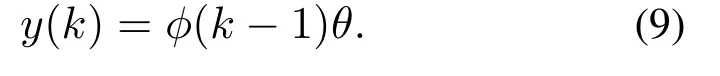
为了解决“数据饱和”问题，本文采用带遗忘因子的递推最小二乘算法(the least square method with forgetting factor)，其算法公式为

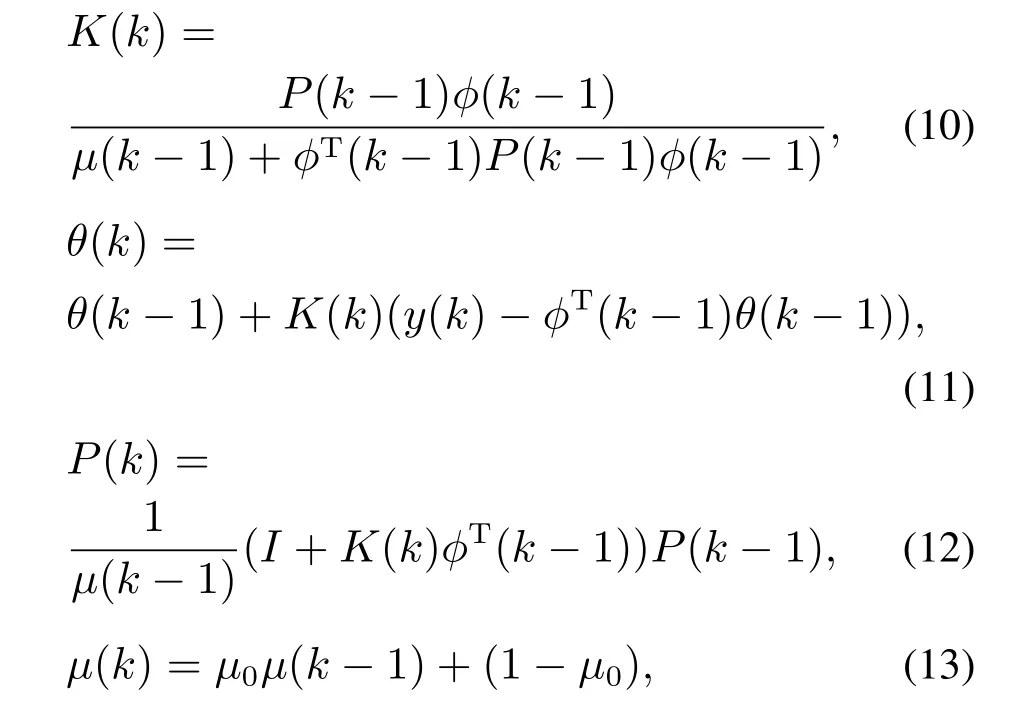
式中 K(k)，θ(k)，P(k)，μ(k)分别为增益矩阵、参数向量、逆矩阵和遗忘因子.注意到上述算法需要事先给定初值θ(0)=0，P(0)=αI，μ0=0.99，μ(0)=0.95，其中α为足够大的正数，本文选用104.

4) 实验结果.

参数收敛曲线如图4所示.图中曲线表示参数向量θ中参数值的变化趋势，当参数值随着递推次数的增加趋于稳定时，认为参数向量达到稳定，FFARMAX模型将通过稳定的参数向量构建.从图4中可以看出，参数向量θ在经过400次迭代后达到稳定.因此，选取迭代400次时的参数向量θ代入式(9)中构建FF-ARMAX模型.

图4 参数收敛曲线Fig.4 Parameter convergence curves

2.2.2 基于傅里叶变换的环境噪声处理

本文中采用的数据均是高炉生产数据，这些数据中叠加的环境噪声会对建模与预测结果产生严重的影响，因此建模之前需要剥离出数据中的高频环境噪声[5].为了验证信号的正确性，需要对数据进行频谱分析，也就是对数据进行傅里叶变换，将数据由时间域转换到频率域，再根据数据的频率特征剥离数据中的噪声.三角函数形式的傅里叶变换(Fourier transform，FT)如下:

式中:x(t)表示信号;an，bn表示傅里叶系数;n=0，±1，±2; ω0=

完成对于数据的傅里叶变换后，可以得到数据的低频特征，然后将数据输入合理的数字滤波器，就可以在保证有效信息不被破坏的情况下，将高频环境噪声除去.数字滤波器又可以分为FIR数字滤波器和IIR数字滤波器，本文采用的是IIR数字滤波器，也称为递归型的数字滤波器，即滤波器当前的输出不仅与当前和以前的输入值有关，而且还与以前的各个输出值有关[11].

2.2.3 数据预处理效果

根据第2.2.1节中FF-ARMAX模型的建立过程，建立修正模型用于消除T25温度数据中存在的测量误差.T25变量的原始数据如图5所示，从图5中可以看出在T25温度数据中不同位置分布着零下温度数据，这印证了表1中T25的数据信息中最小值为-12.5℃这一现象.T25变量经过FF-ARMAX模型消除测量误差，修正结果如图6所示.从图6中可以看出T25原始数据中大量存在的-12.5℃数据被消除，T25变量数据恢复到正常的高炉温度范畴，证明了FFARMAX 模型可以有效消除数据中存在的测量误差.但是，同样可以发现，消除测量误差的高炉数据中仍然存在着大量由环境因素产生的高频噪声，如图6中黑色虚线圈处所示，因此需要去噪处理.根据第2.2.2节，采用傅里叶变换对经过修正的T25温度数据进行数据分析，然后采用IIR数字滤波器进行去噪处理，处理结果如图7所示.从图7 中可以看出，经过去噪处理，图6中T25温度数据存在的环境噪声被有效去除.

图5 未经过数据预处理的T25原始数据Fig.5 T25 data without data preprocessing

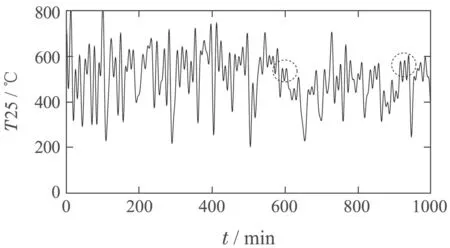
图6 经过FF-AMRAX模型修正的T25数据Fig.6 T25 data corrected by FF-AMRAX model

图7 去噪后的T25修正数据Fig.7 T25 revised data after denoising

图8为经过FF-ARMAX模型修正和去噪处理的T25温度数据与T25原始温度数据的对比图.由图8可知，经过数据预处理后的T25温度数据，在保留数据变化趋势不变的情况下，完全消除了叠加在原始数据中的测量误差，并且最大限度的消除了数据中的环境噪声，使数据能够更加真实的反映高炉的生产过程，为接下来的煤气流预测工作做好了准备.

图8 数据预处理结果Fig.8 Data preprocessing result

3 基于RFMLS-RELM 的高炉煤气流多步预测模型

由于影响高炉煤气流分布的因素众多，并且和其他机器学习算法相比，RFMLS-RELM算法更适用于处理大规模复杂实时环境中的大量数据，对之前的历史数据依赖性比较小，具有比较好的鲁棒性[12].本章首先详细介绍RFMLS-RELM算法，然后介绍采用RFMLS-RELM算法所建立的高炉煤气流模型.

3.1 基于限定记忆的正则化极限学习机

由于高炉内部炉况复杂多变，内部情况无法精确判断，为了应对十字测温数据在不同时刻的变化，煤气流预测模型需要实时读入新数据进行模型训练.但是传统的极限学习机会随着训练样本的增加，历史数据逐渐占据训练数据的大部分，新数据所占比重越来越低，而逐渐失去学习能力，即“数据饱和”问题.即使是权值更新的在线贯序极限学习机(an online sequential extreme learning machine algorithm based on incremental weighted average，WOS-ELM)[13-14]也只能给靠给历史数据添加遗忘因子的办法降低“历史数据”在模型训练过程中的影响，然而此举并不能完全排除历史数据的影响，也就是说，随着时间的推移模型最终还是会出现“饱和问题”.为此本文提出了一种RFMLS-RELM算法.该算法在模型训练过程中每读入一个新样本就会去除一个历史样本，隐含层到输出层的权值矩阵β的学习仅依赖于限定个数的最新样本，从而避免“数据饱和”问题的出现.

RFMLS-RELM算法推导过程如下:

其中:wi=[wi1wi2… wiN]T是随机选择的输入权重，连接第i个隐藏节点和输入节点的权值矢量;bi是第i个隐藏节点随机选择的偏置向量;βi是连接第i个隐藏节点和输出节点的权值矢量;wi·xj表示wi和xj的内积;g(wi·xj+bi)是第i个隐藏节点的输出.

式(15)可以转化成矩阵形式:

H称为隐藏层的输出矩阵，β为隐含层输出权重.为更好的平衡训练误差和输出权重，防止算法陷入“过拟合”，RFMLS-RELM算法引入正则化系数C[15-16]，用于平衡训练误差和输出权重β.因此在求解式(16)中输出权重β时，采用如下公式:

设模型训练数据长度为Q，则RFMLS-RELM模型的隐含层输出矩阵H数学表达式为

其中k表示采样时刻，

首先向模型中添加一个新数据yk+Q，则当前模型中包含k至k+Q时刻共计(Q+1)训练样本，根据公式(17)可推导出基于限定记忆的正则化极限学习机的输出层权值矩阵为，

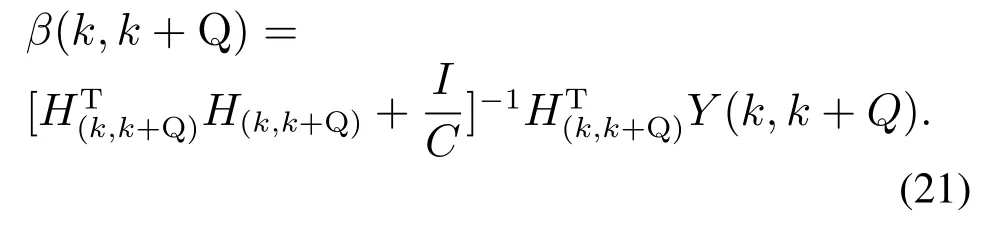
设

由递推最小二乘法的原理可推导出

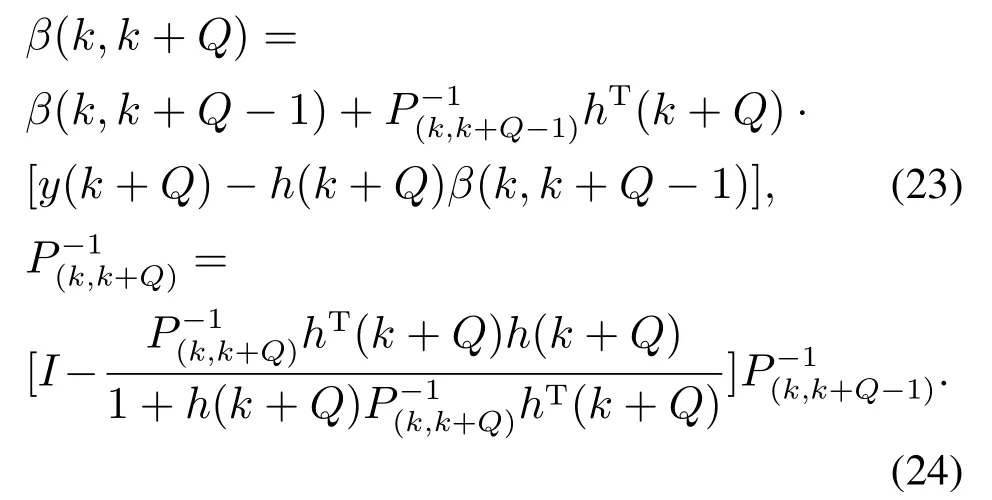
以上，式(23)-(24)就是加入新训练样本时的递推公式.接下来推导剔除旧训练样本时的递推公式.

当矩阵β剔除旧训练样本yk时，模型中包含k+1至k+Q时刻共计Q个训练样本，则有

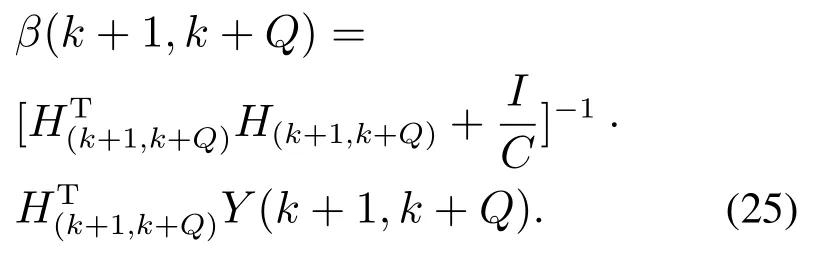
则式(22)改写为

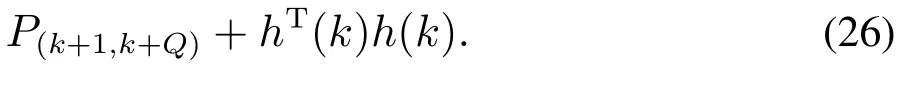
同样由递推最小二乘法的原理可推导出

以上，式(27)-(28)就是剔除旧训练样本时的递推公式.

3.2 基于RFMLS-RELM的高炉煤气流多步预测模型

基于RFMLS-RELM高炉煤气流多步预测模型的建模过程如下所示:

步骤1确定RFMLS-RELM的网络结构.

由第2.1 节的分析可知，以十字测温装置T23，T22，T21，T24，T32，T37，T33和T36作为RFMLS-RELM高炉煤气流预测模型输入层的输入变量，即输入层有8个节点.以T25作为该预测模型的输出变量，即输出层有1个节点.

步骤2建立RFMLS-RELM预测模型.

1) 隐含层节点的激活函数为Sigmoid函数;

2) 隐含层节点个数和正则化因子通过试凑法，经过反复试验确定，并且对输入层到隐含层的权值矩阵和隐含层的偏置向量进行随机赋值;

3) 选取训练样本长度Q，不宜太大;

4) 每当有新样本进入到模型当中时，先利用式(23)-(24)计算β(k，k+Q)和，增加新训练样本的信息;再利用式(27)-(28)计算β(k+1，k+Q)和剔除旧训练样本的信息;

5) 不断迭代直至获得理想的权值矩阵β.

步骤3多步预测.

将经过数据预处理的十字测温数据作为测试样本导入已经训练好的RFMLS-RELM预测模型当中，进行多步预测.

步骤4验证基于FF-ARMAX 和RFMLSRELM的高炉煤气流多步预测模型.

如果运用该模型所得到的预测值与实际测量值的相对误差(relative errors，RE)达到要求，则模型建立完毕.如果不符合要求，则返回步骤2重新建立模型.

4 实例验证和结果分析

引言中提到传统高炉煤气流温度预测模型未能解决的两个问题:

1) 由十字测温装置本身产生的测量误差叠加在温度数据中，这些异常值严重影响了高炉煤气流预测模型的性能，而传统的去噪手段无法有效排除数据中这类由测量误差产生的异常值;

2) 传统高炉煤气流温度预测模型的重点主要集中在优化模型，提高模型预测精度上，而忽视了在工程中的实用性.它们大多属于单步预测，虽然具有很高的精度，但是只能为高炉操作人员提供一分钟甚至几十秒的预测结果，而这对实际操作的帮助十分有限.

针对上述问题，本文基于真实的高炉十字测温数据，将FF-ARMAX和RFMLS-RELM两种算法融合建立高炉煤气流在线多步预测模型.为解决问题1)，采用FF-ARMAX模型消除数据中由测量误差产生的异常值.为检验模型消除异常值的效果，设置检测实验.实验内容为:将经过处理的数据与未经过处理的原始数据分别导入一个基于RFMLS-RELM算法的高炉煤气流温度预测模型，根据其预测结果判断FF-ARMAX 模型对异常值消除效果.为解决问题2)，本文采用RFMLS方法对RELM算法进行优化，提出了一种全新的算法-RFMLS-RELM.接下来首先建立基于RFMLS-RELM算法的高炉煤气流温度预测模型(单步预测模型)，检验该算法在预测煤气流温度上的性能.然后与传统预测模型进行比较，证明RFMLS-RELM预测模型在预测煤气流温度上的优势.最后建立基于RFMLS-RELM算法的高炉煤气流温度多步预测模型，借此解决问题2).

以上所有实验均在具有AMD Ryzen5 1600X 3.6 GHz和8 GB内存的计算机上的MATLAB-2017b中实现.为衡量实验结果的优劣，采用均方根误差RMSE、标准差SD及训练时间和测试时间作为各预测模型的评价标准.以RMSE 最小的为最优结果，若RMSE相同，则比较SD，最后比较时间.

4.1 FF-ARMAX模型对异常值的处理效果实验

为了验证所提方法，论证FF-ARMAX模型对异常值处理的有效性，首先进行FF-ARMAX模型性能检验实验.根据表1可知，T25和T29的原始数据中存在异常值.因此以下检验实验中，模型的输入变量中应当至少包含T25和T29其中一个.

根据上述分析，此次试验选取武钢某高炉实际生产数据.该数据是采样频率为60 s的离散时间序列数据.实验模型的输入输出变量，根据第2.1节的方法，选取T36为输出变量，T27，T26，T24，T25，T37，T23，T33 和T29 为输入变量.实验模型采用RFMLS-RELM 算法建立，参数配置为限定长度Q=50，隐含层节点L=10，正则化系数C=210，激励函数为sigmoid函数.为验证FF-AMRAX模型对异常值的处理效果，实验数据分为两类:经过处理的数据和未经处理的原始数据，各选取1000组数据.其中900组数据作为训练数据，100组数据作为测试数据.为此需要建立两个模型，分别命名为实验模型(处理数据)和实验模型(原始数据).表2为实验模型(处理数据)和实验模型(原始数据)的预测结果.

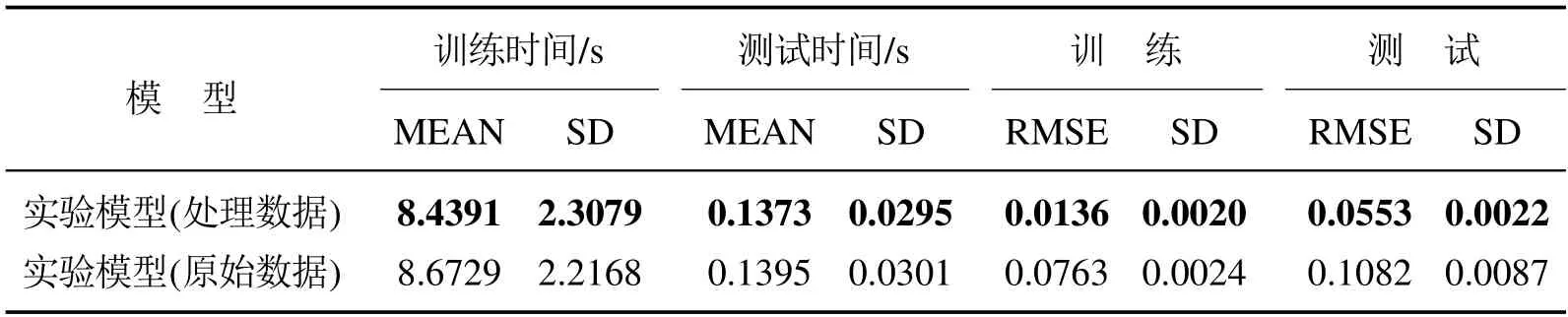
表2 实验模型(处理数据)和实验模型(原始数据)的实验结果Table 2 Experimental results of experimental models(processing data)and experimental models(raw data)

由表2可知，在训练和测试时间上二者相差不多，但是训练和测试RMSE却有很大差距.实验模型(处理数据)无论是在训练阶段还是测试阶段，它的性能表现都强于实验模型(原始数据)，说明原始数据在经过FF-ARMAX模型去除异常值后，对提高预测模型预测精度有很大帮助.证明了FF-ARMAX模型对异常值处理的有效性，解决了上文提到的问题1).

4.2 基于RFMLS-RELM的高炉煤气流温度预测模型实验

4.2.1 RFMLS-RELM性能检测为测试RFMLS-RELM算法在预测高炉煤气流温度时的性能，以及检验RFMLS方法对传统ELM算法和RELM 算法的提升作用，本文在建立RFMLSRELM预测模型的同时，采用ELM算法、RELM算法、WOS-ELM算法和M-ARMAX算法作为对比算法分别建立预测模型.但是RFMLS-RELM算法在实际应用中的性能表现由参数配置决定，因此为了确保预测模型的性能达到最佳，本文先进行调参实验，确定预测模型最佳参数配比.

建立预测模型需要确定RFMLS-RELM的4个参数，即正则化系数C、限定长度Q、隐含层节点个数L和激励函数.正则化系数C分别选取210，215，220，225，230，限定长度Q分别选取50，100，隐含层节点L分别选取10，20，50，100，激励函数选用sigmoid函数.

根据上述分析笔者对RFMLS-RELM预测模型进行调参实验，预测模型经过30次重复试验，取实验结果的RMSE和方差作为预测模型的实验结果，针对不同参数配置的RFMLS-RELM预测模型的实验结果如表3所示.由表3可知，当Q=50，L=50，C=215时，预测结果的RMSE均值最小.故本文选取限定长度Q=50，隐含层节点L=50，正则化系数C=215，激励函数选用sigmoid函数的参数配置作为RFMLSRELM预测模型的最终配置.

表3 RFMLS-RELM模型的调参实验结果Table 3 Results of the adjustment experiments of RFMLS-RELM

在确定RFMLS-RELM预测模型的参数配置后，进行不同预测模型的性能对比.各预测模型的设置如下:

1) ELM模型:建立预测模型需要确定隐含层节点个数L和激励函数.经过试验，最终确定L=10，激励函数为sigmoid函数.

2) RELM模型:建立预测模型需要确定正则化系数C、隐含层节点个数L和激励函数.经过试验，最终确定L=10，C=230，激励函数为sigmoid函数建立RELM预测模型.

3) WOS-ELM模型:建立预测模型确定遗忘因子λ、隐含层节点个数L和激励函数.经过试验，最终确定L=10，λ=0.9，激励函数为sigmoid函数.

4) M-ARMAX模型:该模型的建立过程与第2.2节中FF-ARMAX 模型的建立过程相似，因此MARMAX模型无需参与调参实验，M-ARMAX模型的阶次选择过程和系统辨识过程使用第2.2节中的结果，即np=3，nq=3，参数向量θ一致.

不同预测模型实验对比结果如表4所示.由表4可知，ELM与RELM的训练和测试RMSE大致相同，说明在预测煤气流温度的问题上两者性能接近.然而，在训练时间和测试时间上，RELM均值和方差更小，这说明正则化系数虽然没能提升ELM的性能，但是成功解决了ELM因过度追求训练误差而导致训练时间过长的问题.WOS-ELM的训练和测试RMSE均低于ELM和RELM，说明遗忘因子λ的加入对ELM算法有显著提升.M-ARMAX作为一种常见的系统建模方法，在性能上与ELM和RELM相似，但是不太稳定(测试RMSE的SD高于ELM，说明测试结果变动较大)，但是训练时间远大于两者，因此在实际应用中不具备竞争力.

最后，RFMLS-RELM的训练和测试RMSE是所有预测模型中最好的，证明RFMLS方法对RELM算法的性能有很大提升，而且更加稳定(SD较RELM更小).虽然训练时间和测试时间更长，但是从性能提升的角度上来说是可以接受的，而且高炉本身就是大滞后系统，所以在实际应用中这样的时间成本也是可以接受的.图9为运用RFMLS-RELM预测模型得到的煤气流温度预测结果与实际数据的对比图.图10给出RFMLS-RELM 预测煤气流温度的相对误差.从图9和图10可知RFMLS-RELM能够很好的预测煤气流温度.为了进一步比较各预测模型的性能，图11给出了RFMLS-RELM和4种对比模型的煤气流温度预测值与真实值的对比结果，图12给出预测误差的对比结果.由图11 可以看出，相比其他预测模型RFMLSRELM具有更好的预测效果，并且能够更好的预测煤气流温度的变化趋势.从图12 可以看出，RFMLSRELM预测模型的误差明显小于其他4种预测模型，由此可知RFMLS-RELM具有较高的预测精度.

表4 不同预测模型实验对比结果Table 4 Comparison of experimental results of different prediction models

图9 RFMLS-RELM模型预测结果Fig.9 Prediction results of RFMLS-RELM model

图10 RFMLS-RELM预测误差Fig.10 Prediction errors of RFMLS-RELM model

图11 不同预测模型的预测结果Fig.11 Prediction results of different prediction models

图12 不同预测模型的预测误差Fig.12 Prediction errors of different prediction models

4.2.2 基于RFMLS-RELM算法的多步预测模型性能检测

根据第4.2.1节的实验可知，采用RFMLS-RELM方法建立的高炉煤气流预测模型具有较好的建模精度，对高炉煤气流温度数据具有很高的拟合精度.但是该模型的多步预测精度仍然有待考量，为此本文将建立RFMLS-RELM多步预测模型与由ELM，RELM，WOS-ELM和M-ARMAX算法建立的多步预测模型进行对比，验证RFMLS-RELM模型的多步预测效果.以上多步预测模型使用的数据是采样周期为60 s的离散时间序列数据，因此各多步预测模型的预测步长也为60 s与高炉实际生产数据采集周期相同.为衡量多步预测模型对高炉煤气流温度的预测效果，本文采用相对误差(relative errors，RE)比较各多步预测模型的预测效果，计算每一步的预测值与真实值的RE，当RE ＜10%时，认为该步预测结果为有效预测结果.图13为RFMLS-RELM多步预测模型的预测结果，图14为不同多步模型的预测结果对比图.

由图13可知，RFMLS-RELM单步预测模型的预测结果与真实值非常接近，而多步预测模型会因为预测值替代真实值的缘故，导致每一步预测结果都受到之前预测误差的影响，预测误差不断叠加，故随着预测步数的增加而预测误差越来越大.由图14可知，各多步预测模型在第1步至第3步的预测结果与真实值还比较接近，除了M-ARMAX模型.但是从第4步开始出现较大误差，且随着预测步数的增加误差越来越大，只是不同模型误差增大的速度不同，RFMLSRELM与WOS-ELM增速较ELM和RELM而言相对较慢，而M-ARMAX多步预测模型的预测误差增速远大于其他模型.单纯从图像上，只能看出各多步预测模型的大致表现，为衡量各模型性能需要详细信息.因此表5展示了各多步预测模型的详细预测结果.

图13 RFMLS-RELM多步预测模型的预测结果Fig.13 Prediction results of RFMLS-RELM multi-step prediction model

图14 不同多步预测模型的预测结果Fig.14 Prediction results of different multi-step prediction models

由表5可知，RFMLS-RELM模型的多步预测结果在第1步至第3步时还与单步预测结果接近，但是从第4步开始误差开始不断加大，直至第8步相对误差超过10%.按上文定义，RFMLS-RELM多步预测模型的预测结果中有效预测结果为7步.而ELM多步预测模型与RELM多步预测模型性能表现相近，虽然变化趋势不同但是有效预测结果均为5步，而且随着步数增长，预测结果越偏离真实值，到第10步时甚至有40%以上的误差，这对于实际应用而言是不可接受.WOS-ELM多步预测模型的预测结果相对较好，有效预测结果有6步之多，比较接近RFMLS-RELM模型的性能，但是它的误差增长速度同样很高，第10步时同样也有35%以上的误差.至于M-ARMAX多步预测模型效果较差，有效预测结果只有3 步，而且误差增长速度很高，第10步时相对误差达到86%，这证明了该模型不适用于高炉煤气流温度多步预测.

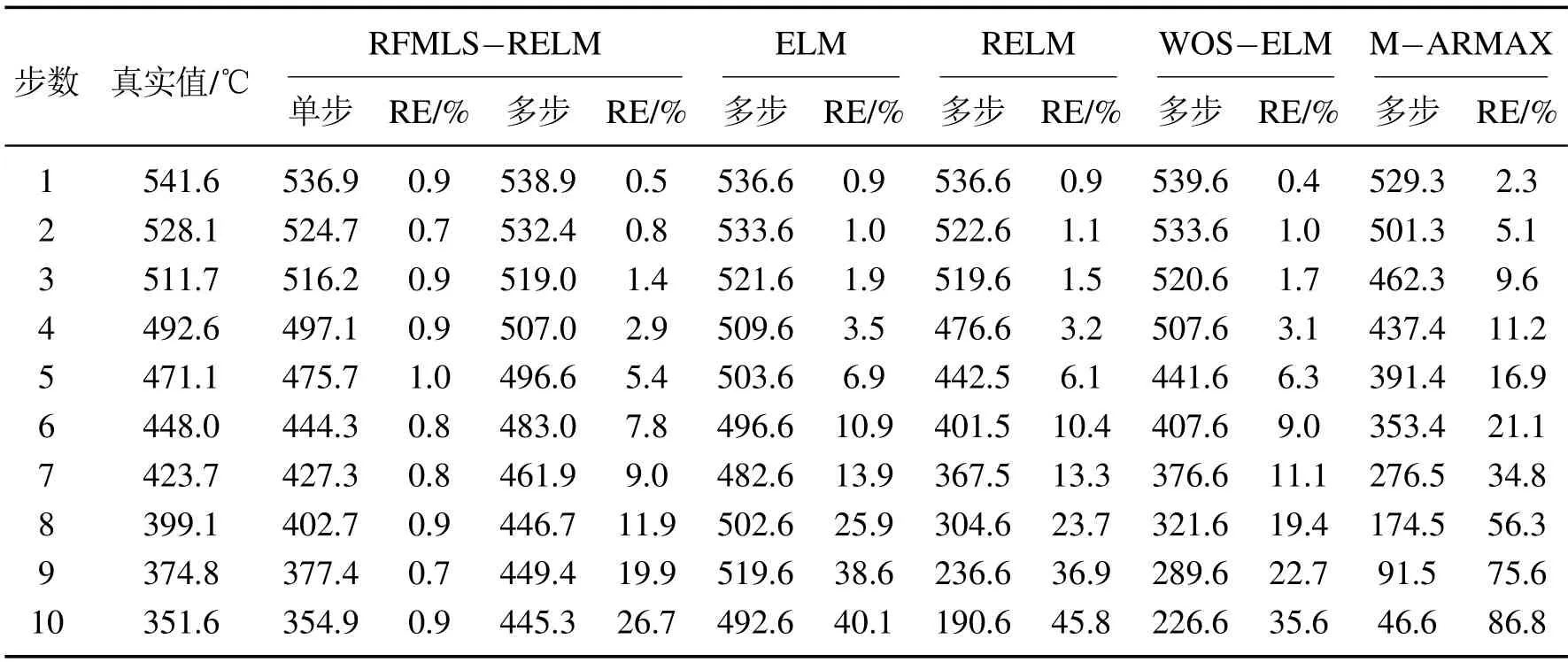
表5 不同多步预测模型的详细预测结果(预测结果单位均°C)Table 5 Prediction results of different multi-step prediction models

由上述实验可知，在多步预测模型中，由于每一步预测结果都会参与到接下来的预测工作中，导致每一步预测产生的预测误差也会叠加到之后的预测结果中，所以多步预测结果的精度必然会随着预测步数的增加而不断增加.本文所提出的RFMLS-RELM算法，在高炉煤气流温度多步预测上，相对其他传统多步预测模型实现了更好的预测效果.虽然无法改变预测误差不断叠加的问题，但是依然取得较好的结果，因此RFMLS-RELM多步预测模型更适用于高炉煤气流温度的多步预测.

5 结论

针对高炉煤气流传统预测模型的缺陷，本文提出了一种基于FF-ARMAX和RFMLS-RELM的高炉煤气流多步预测模型.在数据修正方面，建立FFARMAX模型消除原始数据中因十字测温装置失效或损坏导致的测量误差，同时采用傅里叶变换法消除数据中叠加的环境噪声.最后采用RELM算法进行多步预测，并且运用RFMLS优化RELM隐含层到输出层的权值矩阵，消除了历史数据对模型的影响，避免了“数据饱和”问题的出现.对比试验表明，该算法在应用于高炉煤气流预测时，预测精度更高，因此该算法适用于对高炉煤气流分布状况的多步预测.同时多步预测实验结果表明，该模型虽然仍旧无法完全解决预测误差随预测步数的增加而不断叠加的问题，但相较于其他传统预测模型能够获得更多的有效预测步数，实现更高的预测精度，为建立更加精确的高炉料面温度场提供了可能，为高炉操作人员分析炉况提供了有效的帮助和支持.