Finite Element Modeling and Parametric Analysis of Pavement Dynamic Responses under Moving Vehicle Load

，

1.Civil Engineering College，Tianjin Chengjian University，Tianjin 300384，P.R.China；

2.College of Civil Aviation，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，P.R.China；

3.College of Airport Engineering，Civil Aviation University of China，Tianjin 300300，P.R.China

（Received 8 March 2019；revised 5 May 2019；accepted 25 May 2019）

Abstract: This paper intends to develop finite element models that can simulate vehicle load moving on pavement system and reflect the pavement response of vehicle and pavement interaction. We conduct parametric analysis considering the influences of asphalt concrete layer modulus and thickness，base layer modulus and thickness，and subgrade modulus on pavement surface displacement，frequency，and strain response. The analysis findings are fruitful. Both the displacement basin width and maximum value of dynamic surface displacements are larger than those of static surface displacements. The frequency is positively correlated with the pavement structure moduli，and negatively correlated with the pavement structure thicknesses. The shape of dynamic and static tensile strain is similar along the depth of the pavement structure. The maximum value of dynamic tensile strain is larger than that of static tensile strain. The frequency of entire pavement structure holds more significant influence than the surface displacement and strain do. The subgrade modulus has a significant effect on surface displacement，frequency and strain.

Key words：pavement dynamic response；vehicle load；surface displacement；frequency；strain

0 Introduction

Finite element（FE）models play an important role in explaining the pavement response subjected to moving vehicle loading. Garcia et al.［1］explicated that transverse tensile strains were more responsible for fatigue cracking compared with longitudinal strain in terms of strain magnitude and pulse dura⁃tion. Picoux et al.［2］predicted the asphalt pavement displacement response with the stationary transient load placing on the asphalt surface.Wang et al.［3］sim⁃ulated vehicular loading as moving transient load to study the strain response of the asphalt pavement.Ozer et al.［4］researched the effect of bonding condi⁃tions on the critical strains in hot-mix asphalt（HMA）overlaid Portland cement concrete（PCC）pavements by laboratory experiment，field testing，and numerical analysis. They found HMA tensile strains can be significantly amplified with less stiff in⁃terface properties which correspond to decreasing bonding strength. Wang et al.［5］and Al-Qadi et al.［6］applied the viscoelastic model of asphalt pavement to investigate the effect of wheel load，vehicle speed，pavement structure，and temperature on modulus distribution in the granular base layer. Patil et al.［7］proposed a solution algorithm of three-dimensional fi⁃nite element analysis to analyze the dynamic re⁃sponse，including displacement and velocity，of pavement structure with moving vehicle loading.The study by Dong and Ni［8］showed that vertical compression strain at the top of the asphalt layer was a key index to evaluate the pavement dynamic re⁃sponse based on the moving transient load. Arraiga⁃da et al.［9］presented the asphalt pavement response under moving constant load and compared the results with those of accelerated pavement testing. Chun et al.［10］studied the longitudinal strain response at the bottom of asphalt layer under moving constant load.Ramos-García et al.［11］researched the displacement response of the asphalt pavement with modelling the vehicular loading as moving constant load.Li et al.［12］developed the finite element models to simulate pavement responses under falling weight deflectome⁃ter（FWD） loading and moving vehicle loading.They explored the influence of vehicle speed and pavement depth on pulse durations of compressive stresses for two asphalt pavement structures. Ta⁃herkhani et al.analyzed the effect of tire configuration on the responses of the geogrid-rein forced asphalt pavements under moving transient load［13］.

Although previous research has achieved signif⁃icant advances，the frequency response of pavement structure has not been thoroughly investigated and quantified.Therefore，to better understand the pave⁃ment structure dynamic response and performance under moving vehicle load，all pavement indicators，displacement，frequency and strain，need to be in⁃vestigated and quantified using the finite element（FE）models. The objectives of this study have two folds. The first is to develop and verify the FE mod⁃el that can accurately reflect pavement displace⁃ments，frequencies，and strains. The second is to analyze the important factors that should be consid⁃ered in the FE models，including asphalt concrete（AC）layer modulus and thickness，base layer mod⁃ulus and thickness，and subgrade modulus. The de⁃velopment of FE models can directly benefit the AC pavement structure strength evaluation and perfor⁃mance prediction.

1 Finite Element Modeling

1.1 Vehicle model

For the results to be more truly representative of actual pavement vibrations，ANSYS 10.0 simula⁃tion software was used to create vehicle⁃road mod⁃els in which the mass of the suspension system was assigned to the front and the rear axles of the vehicle in a mass ratio of 1∶4. The testing vehicle was mod⁃eled as a three-dimensional mass⁃spring⁃damper sys⁃tem with seven degrees of freedom（DOFs），as shown in Table 1 and Fig.1. The tandems at the drive and the rear axles of the test vehicle were lumped as single wheels for simplicity. Therefore，this model consisted of five rigid masses that repre⁃sented the truck and its four wheels. The vehicle was assigned three DOFs corresponding to the verti⁃cal displacement at the mass center，pitching rota⁃tion，and rolling rotation. Each wheel was modeled as a lumped mass with only vertical displacement.The vehicle was represented by beam elements（MPC184）.The suspension and non-suspension sys⁃tems and the moments of inertia of the pitching and rolling rotations were represented by mass elements（Mass21）. The spring and damper were represented by a spring⁃damper element（Combine14）.

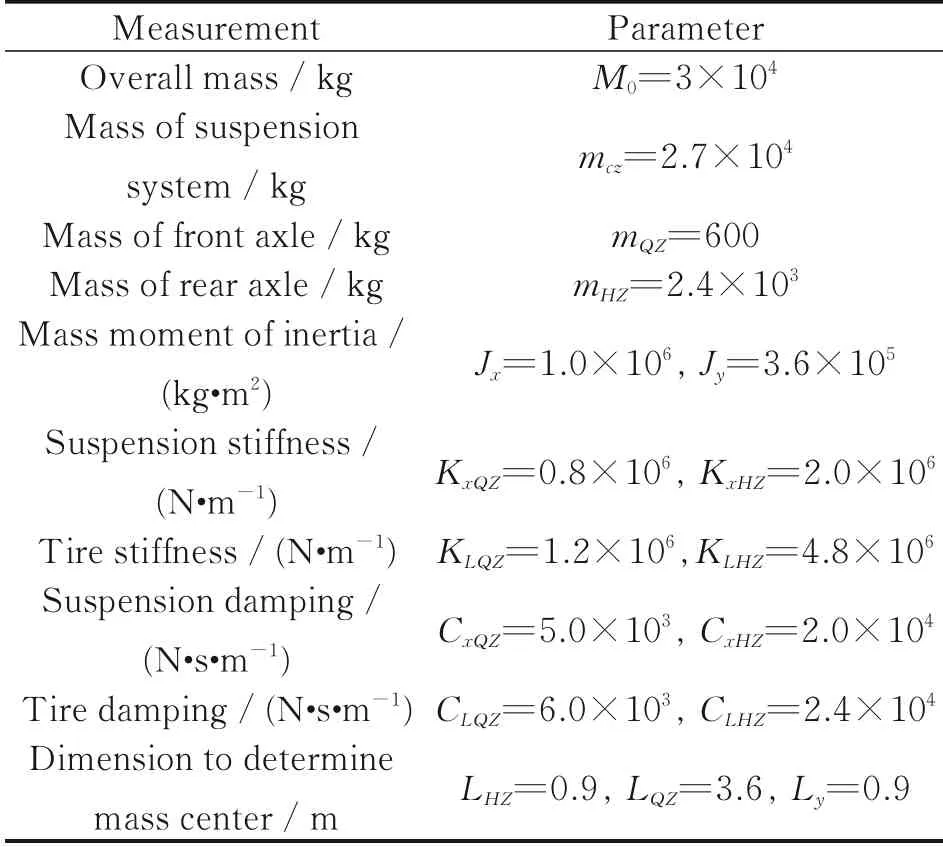
Table 1 Parameters of the test vehicle

By using D’Alembert’s principle，the equa⁃tions of motion for the vehicle are

whereZ0，Z1，Z2，Z3，Z4，Z5，Z6，Z7，andZ8are the vertical displacements of the salient points of the test vehicle. Furthermore，Z1=Z0+θxLy+θyLHZ，

Z2=Z0-θxLy+θyLHZ，Z3=Z0+θxLy-θyLHZ，Z4=Z0-θxLy-θyLHZ，Q1=Z1-Z5，Q2=Z2-Z6，Q3=Z3-Z7，Q4=Z4-Z8，whereθxandθyrepresent the pitching rotation；andZ9，Z10，Z11，andZ12the road roughness at each of the four wheels，respectively.

Fig.1 Analytical model of the test vehicle with seven DOFs

1.2 Pavement structure model

The actual pavement structure is a layered ar⁃chitecture，and each structure layer has its own resil⁃ient modulus and Poisson’s ratio. The pavement structure model of elastic layered system can reflect the actual response of pavement structure. Because pavement structure layers are very complicated，some reasonable assumptions should be made in pavement structure model：

（1）Pavement structure layers are continuous，and the material of each layer is homogeneous and isotropic.

（2）The stress and displacement are continu⁃ous in each structure layer.

（3）The stress and displacement in horizontal direction is zero in the infinity point for each pave⁃ment structure layer. The stress and displacement in depth direction is zero in the infinity point for sub⁃grade.

Table 2 Properties of the base layer and the subgrade

However，the infinite entity structure of pave⁃ment model is not established by FE method.The fi⁃nite dimension of pavement model was selected to be 23 m×16 m（length × width）and the depth of subgrade was to be 9 m by calculation and analysis，because the large enough model can reduce the influ⁃ence of boundary conditions. In the FE model，the eight-node，hexahedral elements with improved cal⁃culation accuracy and efficiency（soild45）were used for the mesh generation of pavement structure. The size of mesh element was 23 m×16 mm（length ×width）for the asphalt concrete layers and 46 m×32 mm（length × width）for the base layer and sub⁃grade. The mash element thicknesses were selected at 10% of the thickness of the asphalt and the base layers，and 30 mm for the subgrade. The bottom of the subgrade was restricted by all degrees of free⁃dom. The edges of the subgrade and the base layer were constrained in the length-direction and the width-direction.The asphalt concrete layer was stabi⁃lized by the interaction with the base layer and the weight of asphalt concrete layer. Table 2［14-16］pres⁃ents the properties of the pavement structure layers used in the finite element model.

1.3 Vehicle⁃pavement model validation

A validation study for the developed FE model was conducted with field measurement results under the traffic speed deflectometer（TSD）and the roll⁃ing wheel deflectometer（RWD）testing. The AC pavement section selected for this study was the mainline and closed-loop low-volume road（LVR）of the MnROAD in Wright County，USA. The ma⁃terial properties of pavement structures were ob⁃tained from the laboratory testing，TSD and RWD testing，as shown in Table 3［17］. The dynamic load of rear axle at the speed of 13.14 m/s for TSD test⁃ing is shown in Fig.2［17］. And the wheel-pavement contact area of rear axle was 0.0736 m2. The static and the dynamic contact pressures of RWD testing are 689.5 kPa and 917.04 kPa，respectively［17］.

Table 3 Pavement structure layer properties used in the finite element method[17]

Fig.2 Dynamic wheel load for TSD testing[17]

The above data were directly input into the ANSYS 10.0 simulation software to establish the FE model of wheel-pavement response. In the FE model，the AC pavement structures were simulated as the elastic layered system. The finite dimension of pavement model was selected to be 23 m×16 m（length × width）and the depth of pavement struc⁃ture was as shown in Table 3. The eight-node，and the hexahedral elements with improved calculation accuracy and efficiency（soild45）were used for the mesh generation of pavement structure. The size of mesh element was 23 m×16 mm （length ×width） for the AC layers and 46 m×32 mm（length × width）for the base layer and the sub⁃grade. The mash element thicknesses were selected at 10% of the thickness of the AC layers，the base layers and the subgrade. The bottom of the sub⁃grade was restricted by all degrees of freedom. The edges of the subgrade and the base layer were con⁃strained in the length-direction and the width-direc⁃tion. The AC layer was stabilized by the interaction with the base layer and the weight of the AC layer.The vehicle load was simplified by using the mea⁃sured dynamic loading amplitude in Fig.2 within the tire imprint area of 0.073 6 m2in the TSD testing.The vehicle load was simplified by using contact pressures in the RWD testing. To simulate the movement of a wheel at a certain speed，the con⁃cept of a continuously moving load was used. In this approach，the wheel loading imprint area is gradually shifted over the pavement. The step time was decided by the wheel moving speed and ele⁃ment lengths.

These data were directly used in the FE model as the input and the accuracy of prediction results was and compared to field measurements examined for model validation. Fig.3 compares the measured and the predicted surface displacement. The results show that the FE model of cell 34 adequately cap⁃tured the shape of measured displacements，while the finite element model displacement basins were wider than the measured values of cell 19. It might be caused by the transverse wheel wander. The FE model results of dynamic load had good agreements with the maximum displacement. Fig.4 compares the predicted and the measured surface velocities（maximum from field trials）. Although all finite ele⁃ment model case results had similar shapes as the measured ones，the predictions of dynamic load were closer to the measured velocities. Fig.5 com⁃pares the measured and the predicted longitudinal strains. The calculated longitudinal strains from the finite element model of dynamic load matched well with the measured values. In a word，the realistic assumption of vehicle-pavement interaction and dy⁃namic load pattern resulted in smaller differences be⁃tween the measured and the calculated displace⁃ments，the velocities and the longitudinal strains.Hence，the vehicle-pavement model can predict the pavement response with dynamic vehicle load mov⁃ing on different asphalt pavements.

Fig.3 Predicted and measured surface displacements in TSD testing

Fig.4 Predicted and measured surface velocities in TSD testing

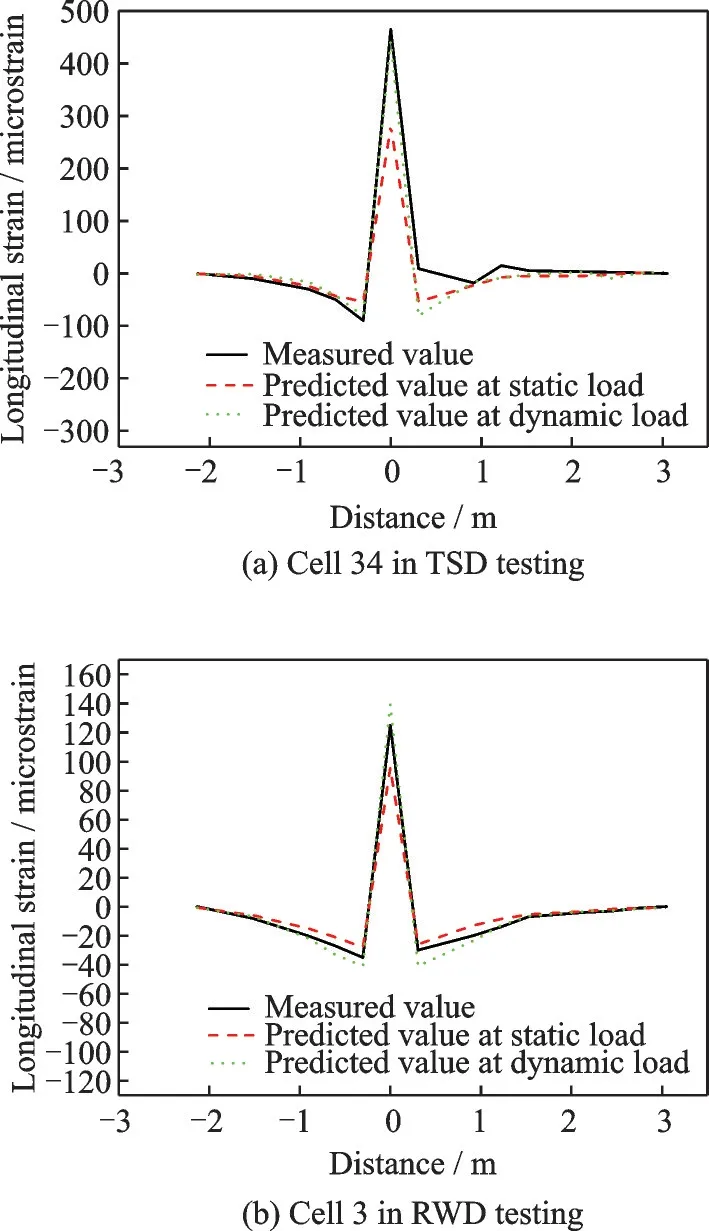
Fig.5 Predicted and measured longitudinal strains for cell 34 in TSD testing and for cell 3 in RWD testing

2 Results and Analysis

The influence of pavement structure modulus and thickness on pavement responses，including sur⁃face displacement，frequency and strain，under vehi⁃cle dynamic loading were investigated using the de⁃veloped FE model. The surface displacement can represent structure behavior of the entire pavement system［12］. It has been widely accepted that tensile strains at the bottom of asphalt concrete layer are re⁃lated to fatigue cracking distress and tensile strains at the top of subgrade are related to rutting. In addi⁃tion，the frequency was used to indicate the vibra⁃tion performance of vehicle and pavement interac⁃tion，because the frequency can better represent the integrity of the pavement system than surface dis⁃placement and strain do.

2.1 Surface displacement analysis

Fig.6 shows the influences of the asphalt con⁃crete layer modulus and thickness，the base layer modulus and thickness，and the subgrade modulus on surface displacements. When the parameter of pavement structure keeps the same，both the dis⁃placement basin width and the maximum value of dynamic surface displacements are larger than those of static surface displacements.

In Figs.6（a）and（b），the shape of surface dis⁃placement is similar and the maximum of surface dis⁃placement is various at different asphalt concrete lay⁃er moduli and thicknesses. When the asphalt con⁃crete layer modulus increases from 2 000 MPa to 4 000 MPa，the maximum of dynamic surface dis⁃placement decreases 0.11 mm. And as the asphalt concrete layer modulus increases from 4 000 MPa to 6 000 MPa，the maximum of dynamic surface dis⁃placement decreases 0.06 mm. However，the maxi⁃mum of dynamic surface displacement decreases 0.10 mm with the asphalt concrete layer thickness in⁃creasing from 0.15 m to 0.35 m. Since the addition of asphalt concrete layer modulus and thickness is benefi⁃cial to improving the strength of the entire pavement system and reducing the surface displacement. Fur⁃thermore，the asphalt concrete layer modulus of more than 4 000 MPa has little effect on the surface displace⁃ment.Therefore，the blindly increasing of asphalt con⁃crete layer modulus might have minimal effectiveness on the reduction of surface displacement and the im⁃provement of pavement structure performance.

In Figs.6（c）and（d），the maximum value and decreasing amplitude of surface displacement de⁃creases with the increase of base layer moduli and thicknesses. When the base layer modulus increases from 200 MPa to 1 800 MPa，the maximum of dy⁃namic surface displacement decreases 0.04 mm uni⁃formly，and the dynamic surface displacement in the middle of two wheels decreases 0.07 mm. As the base layer modulus increases from 1 800 MPa to 3 400 MPa，the maximum of dynamic surface dis⁃placement decreases 0.034 mm uniformly，and the dynamic surface displacement in the middle of two wheels decreases 0.035 mm. Hence，the surface dis⁃placement in the middle of two wheels is close to the maximum of surface displacement as the increase of the base layer moduli. Especially，the surface dis⁃placement in the middle of two wheels is similar to the maximum of surface displacement with the base layer modulus more than 1 800 MPa. Meanwhile，surface displacement decreases with the increase of the base layer thickness. When the base layer thick⁃ness is more than 0.30 m，the increasing amplitude of surface displacement is smaller. Hence，the base layer modulus of 1 800 MPa and the base layer thick⁃ness of 0.30 m can help to ensure quality and save cost for the pavement engineering.

Fig.6 Surface displacement influenced by different factors

In Fig.6（e），both the shape and the maximum of surface displacement vary with different subgrade moduli. The maximum of the dynamic surface dis⁃placement reduces 0.26 mm with the subgrade modu⁃lus from 60 MPa to 180 MPa，and decreases 0.03 mm as the subgrade modulus increasing from 180 MPa to 220 MPa. Nevertheless，when the sub⁃grade modulus varies from 60 MPa to 180 MPa，the dynamic surface displacement in the middle of two wheels decreases 0.29 mm.As the subgrade modulus varies from 180 MPa to 220 MPa，the dynamic sur⁃face displacement at the middle of two wheels de⁃creases 0.05 mm. Thereby，the subgrade moduli have a significant influence on the maximum of sur⁃face displacement and the surface displacement in the middle of two wheels when the subgrade modulus is less than 180 MPa. In other words，it is inadvisable to reduce surface displacements and promote the pavement performance by blindly increasing sub⁃grade modulus.

In a nutshell，these findings indicate that the in⁃fluence of subgrade modulus on surface displace⁃ment is more remarkable than those of asphalt con⁃crete layer modulus and thickness，and base layer modulus and thickness. In addition，asphalt con⁃crete layer modulus，base layer modulus and thick⁃ness，and subgrade modulus have an optimal value.

2.2 Frequency analysis

Fig.7 shows the acceleration-time histories and frequency spectrum analysis of acceleration. The ac⁃celeration-time histories of pavement free vibration were obtained by taking impulsive load as excitation source and the central point of pavement as sam⁃pling position. The method of fast Fourier transform was applied to obtain the frequency spectrum analy⁃sis of acceleration. The sampling frequency must be more than twice of the original signal frequency to reflect the actual frequency domain signals，which is required in sampling theorem. Moreover，the fre⁃quency range of pavement vibration was mainly 0 Hz to 30 Hz. Therefore，the sampling in this study was selected as 60 Hz. In other words，300 acceleration signals were collected in 5 s.

Fig.8 shows the influence of the asphalt con⁃crete layer modulus and thickness，the base layer modulus and the thickness，and subgrade modulus on the frequency of pavement structure. Figs.8（a），（b）indicate that the frequency increases 0.24 Hz as the asphalt concrete layer modulus increasing from 2 000 MPa to 6 000 MPa，and 0.48 Hz as the asphalt concrete layer thickness increasing from 0.35 m to 0.15 m. Thereby，the frequency is positively corre⁃lated with asphalt concrete layer moduli，and nega⁃tively correlated with asphalt concrete layer thick⁃nesses. Moreover，the increasing of asphalt concrete layer thickness causes the decreasing of the pave⁃ment frequency，which is easy to make the frequency of pavement structure being close to that of vehicle load and contribute to the resonance of pavement structure and vehicle load. It is not feasible for im⁃proving the strength of pavement structure by blindly increasing the asphalt concrete layer thickness.

Figs.8（c）and（d）show that influences of base layer moduli are the same as those of asphalt concrete layer moduli，and effects of base layer thicknesses are similar to those of asphalt concrete layer thicknesses.The frequency of pavement structure increases with the addition of the base layer modulus and the reduc⁃tion of the base layer thickness. The influence of the asphalt concrete layer modulus on the frequency is greater than that of the base layer modulus.

Fig.8（e）indicates that the effect of subgrade moduli on frequency is more significant than those of asphalt concrete layer moduli and thickness，and base layer moduli and thickness. The increase of the subgrade modulus is helpful to improve the frequen⁃cy of pavement structures. Furthermore，when the subgrade modulus varies from 60 MPa to 220 MPa，the frequency increases about 0.97 Hz. It means that the subgrade modulus is the critical factor for pave⁃ment structure performance. Attentions should be paid to subgrade moduli in the design and mainte⁃nance of pavement structure.

Fig.8 Frequency influenced by different factors

The recent advances in optoelectronic oscilla⁃tors，arbitrary waveform generation，photonic mix⁃ing，phase coding，filtering，beamforming，analogto-digital conversion，and stable RF signal transfer are described. Challenges in implementation of these components and subsystems for meeting the requirements of the radar applications are discussed.

2.3 Strain analysis

Fig.9 shows the influence of the asphalt con⁃crete layer modulus and thickness，the base layer modulus and thickness，and the subgrade modulus on tensile strains. When the parameter of pavement structure keeps the same，the dynamic tensile strain is larger than the static tensile strain. The shapes of the tensile strain in Fig.9 are similar and the maxi⁃mum value of tensile strain is at the bottom of asphalt concrete layer for different pavement structures. The reason is that the tensile strain decreases with the in⁃crease of pavement structure depth，and the surface of asphalt concrete layer is mainly compressive strain. Therefore，tensile strains at bottom of the as⁃phalt concrete layer are important to evaluate the bot⁃tom-up cracking distress.In Figs.9（a），（c），both the asphalt concrete layer and the base layer moduli have a negative relationship with tensile strains.The maxi⁃mum of dynamic tensile strain decreases about 74 με as the asphalt concrete layer modulus increasing from 2 000 MPa to 6 000 MPa，and 80 με as the base layer modulus increasing from 200 MPa to 3 400 MPa.

Since the main focus is the comparison of ten⁃sile strain（shape and maximum value），the plots are shifted to align so that the maximum tensile strain locations can coincide. In Figs.9（b）and（d），when the asphalt concrete layer thickness increases from 0.15 m to 0.30 m，the maximum of dynamic tensile strain decreases 51 με. As the base layer thickness increases from 0.20 m to 0.35 m，the max⁃imum of dynamic tensile strain decreases 38 με.However，the maximum of dynamic tensile strain decreases 11 με with the asphalt concrete layer thick⁃ness rising from 0.30 m to 0.35 m，and 10 με as the base layer thickness growing from 0.35 m to 0.40 m. Therefore，the influence of the asphalt con⁃crete layer thickness on tensile strain is greater than that of base layer thickness.

In Fig.9（e），the shape and maximum of tensile strains vary largely when the subgrade modulus is more than 60 MPa. For example，the maximum of dynamic tensile strain decreases about 19 με as the subgrade modulus rising from 60 MPa to 100 MPa，and the maximum of dynamic tensile strain decreases 33 με as the subgrade modulus rising from 100 MPa to 220 MPa. Thereby，the influence of subgrade moduli on the tensile strain is not negligible.

In conclusion，the surface displacement，fre⁃quency and strain of pavement structure are all effect⁃ed by parameters of pavement structures. Subgrade moduli have a significant influence and could not be disregarded. Fig.9 also shows that tensile strains have a turning point at the distance of 6 m（3 m away from the top of the subgrade）. The tensile strain at the distance of 6 m to 9 m varies larger and changes faster than that at the distance of 1.3 m to 6 m. Pa⁃rameters of pavement structures have little influence on tensile strain at the distance of 1.3 m to 6 m.

Fig.9 Strain influenced by different factors

3 Conclusions

In this study，FE models were developed to simulate asphalt pavement dynamic response under moving vehicle loading. The parametric analysis findings demonstrate subgrade moduli are the impor⁃tant factor for the surface displacement，frequency and strain. Asphalt concrete layer moduli have small influence on the surface displacement，frequency and strain. When the parameter of pavement struc⁃ture keeps the same，both the displacement basin width and the maximum value of dynamic surface displacements are larger than those of static surface displacements. The frequency response of the entire pavement structure is larger than the response of the surface displacement and strain，especially the ef⁃fect of subgrade moduli. The frequency increases with the addition of pavement structure layer modu⁃lus and the reduction of pavement structure layer thickness. The shapes of the dynamic and the static tensile strains are similar. With the same parameters of a pavement structure，the maximum value of the dynamic tensile strain is larger than that of the static tensile strain. The developed FE model successfully captures the surface displacement，frequency，and strain of asphalt concrete pavement.