基于HB样条的平面大变形结构动力学等几何分析

2020-07-15荣吉利熊丽园刘铖辛鹏飞刘志超

北京理工大学学报 2020年6期

荣吉利，熊丽园，刘铖，辛鹏飞,2，刘志超

(1.北京理工大学宇航学院，北京 100081；2.北京空间飞行器总体设计部，北京 100094；3.空间物理重点实验室，北京 100076)

为了实现计算机辅助设计(CAD)与计算机辅助工程(CAE)的融合，Hughes等[1]把非均匀有理B样条(NURBS)基函数引入到等参有限元分析中，建立了等几何分析方法(IGA).与传统有限元[2-3]拉格朗日多项式插值方法不同，等几何分析方法将CAD中样条基函数作为插值函数直接用于有限元分析中，能够精确描述复杂几何构型，消除了几何误差.

在等几何分析中，B样条和NURBS是两类常用的样条基函数.对于2维或3维问题，多变量B样条与NURBS通常采用张量积形式构造，其网格局部加密将会导致全局网格的变化，无法实现局部细化，极大地降低了等几何分析方法的计算效率.而为实现网格局部细化及自适应网格，多种可局部加密的样条函数应运而生，例如，T样条、LR样条(Local Refined-Splines)以及层次B样条(Hierarchical B-Splines，简称HB样条).在CAD领域，Sederber[4]首次提出了T样条概念，允许网格T节点的存在，实现了网格的局部细化.Bazilevst[5]将T样条引入等几何分析，研究表明T样条基函数可能存在线性相关性，将导致系统刚度矩阵严重数值病态.同时，Dokken等[6]推广NURBS，提出了LR样条，它通过在张量积形式的B样条网格中插入节点线段(一整条节点线中的一段)，实现网格局部细化.但LR样条基函数仍可能存在线性相关性，并且该样条基函数构造较为复杂.此外，Forsey与Bartels[7]提出了层次B样条(HB样条)，HB样条基函数由一系列嵌套的张量积样条基函数构成，丰富了样条模型的局部特性.Vuong[8]给出了一种构造HB样条空间的一组线性无关的基函数的方法，并将其应用在自适应等几何分析中，实现了L型区域静态热传导问题的网格局部细化.Henning等[9]将HB样条应用于裂纹扩展问题的等几何分析中，在裂纹扩展过程中构造了基于HB样条的自适应网格，结果表明该方法能够有效地提高计算效率.HB样条具有嵌套性，它的基函数是由多个细分层的基函数组成，这使得HB样条在自适应等几何分析中表现出巨大的优势.此外，HB样条的构造简单，这些优点使得HB样条成为等几何分析的研究热点之一.上述研究大多仅涉及结构静力学问题，而尚无关于等几何分析处理结构动力学问题中局部细化算法研究.

在等几何分析中，为了实现IGA单元形函数的统一化，Borden等[10]首次提出了NURBS的贝塞尔提取方法(Bézier extraction)，采用描述贝赛尔曲线的伯恩斯坦基函数表示NURBS基函数，使得每个NURBS单元的形函数都相同，由此可以将等几何分析程序与传统有限元程序融合.之后，Scott等[11]将贝塞尔提取应用于基于T样条的等几何分析中.D’Angella等[12]将贝塞尔提取用于HB样条中，提出了多层贝塞尔提取方法(multi-level Bézier extraction)，并证明该方法适用于非线性问题和并行计算.

为此，在上述研究基础上，探讨了大变形平面结构动力学问题中的网格自适应算法，给出了基于HB样条的网格局部加密算法，并分析了HB样条基函数的构造以及多层贝塞尔提取方法.

1 HB样条和多层贝塞尔提取算法

1.1 贝塞尔曲线、B样条和NURBS

一条p阶贝塞尔曲线是p+1个伯恩斯坦基函数的线性组合，其表达式为

(1)

式中：Pi为贝塞尔控制点；ξ∈[-1,1]为贝塞尔单元的参数坐标.伯恩斯坦基函数Bi,p可表示为

(1-ξ)p-(i-1)(1+ξ)(i-1),

(2)

其中，1 ≤i≤p+1.从伯恩斯坦基的表达式可以看出，给定基函数的阶数p,p+1个伯恩斯坦基函数可唯一给出，即每个单元上的基函数都相同，与有限元方法中的单元形函数具有类似的性质.

此外，一个单变量p阶B样条基函数定义在一个递增的节点矢量Ξ上，

Ξ=[ξ1ξ2…ξn+p+1],

(3)

式中：ξ为量纲一参数坐标；n为基函数个数.节点矢量组成的区域称为参数域，参数域含有的节点矢量的个数决定了几何模型的维度.基于Cox-de Boor递推公式，一个p阶B样条基函数可表示为两个p-1阶B样条基函数的线性组合为

(4)

其中，规定0/0=0.第i个基函数Ni,p与ξi,ξi+1,,ξi+p+1共p+2个节点矢量元素有关，这些元素组成的区间[ξi,ξi+p+1]称为基函数Ni,p的支持域，记任意基函数f的支持域为suppf.B样条基函数连续性由节点矢量元素重复度决定，对于重复度为k的节点，基函数Cp-k连续，而在节点之间C∞连续.一般而言，对于开放式节点矢量，第1个结点和最后一个结点的重复度为k=p+1.

在B样条基函数基础上，引入权因子可推广至NURBS样条基函数，NURBS基函数除具备B样条良好性质外，还能精确描述各类二次曲线与曲面，例如圆、双曲线、椭圆面等.一个p阶NURBS样条基函数为

(5)

上述单变量样条函数可方便推广至多维情况，以2维问题为例，双变量张量积形式的NURBS基函数为

(6)

式中：wi,j为权因子；Ni,p(ξ)和Mi,q(η)分别为p阶和q阶B样条基函数.由此，NURBS曲面中任意一点的位置坐标矢量可表示为

(7)

式中：{Pi,j}(i=1,2,,n，j=1,2,,m)为曲面控制点，Ξ=[ξiξ2…ξn+p+1]和Η=[η1η2…ηm+q+1]分别为ξ和η方向的节点向量.

在等几何分析中，对于1维情况，将节点矢量中两个相邻的不等节点区间e=[ξi,ξi+1],ξi≠ξi+1视为一个单元.由于参数域与几何模型存在映射关系，这些单元把实际物理模型划分为多个一一对应的子区域.图1为一个定义在节点矢量Ξ1=[0 0 0 1 2 2 3 4 4 4]的单变量B样条基函数分布图，该节点矢量包含4个单元，单元e2=[1,2]用点划线表示.图2表示定义在相同节点矢量Ξ2×Ξ2上的双变量基函数分布图，Ξ2=[0 0 0 1 2 3 4 4 4].

1.2 贝塞尔提取与节点插入算法

在传统有限元方法中，一类单元一般具有相同的形函数.然而，在等几何分析中，采用的B样条基函数定义在全局的节点矢量上，单元的基函数通常不同.为了实现等几何分析程序与现有的有限元程序相融合，贝塞尔提取技术被广泛应用于各类样条基函数，如B样条，NURBS以及T样条.贝塞尔提取的核心思想是采用节点插入算法，实现伯恩斯坦基函数来表示全局定义下的B样条基函数.

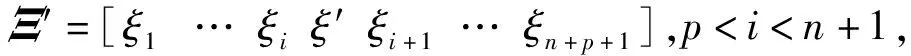
(8)

其中，

(9)

为了保持节点插入中几何构型不变，应满足

(CTP)TB(ξ)=PTCB(ξ).

(10)

因此，B样条基函数与伯恩斯坦基函数之间的关系为

N(ξ)=CB(ξ),

(11)

其中，线性算子C称为全局贝塞尔提取算子[11]，它能将任意阶连续的B样条基函数表示成分段C0连续的伯恩斯坦基函数的线性组合.单元贝塞尔提取算子Ce可从全局贝塞尔提取算子C获得.由此，单元B样条基函数可表示为

(12)

(13)

其中，两个矩阵的克罗内克积A⊗B的表达式为

(14)

上述方法可直接推广至NURBS基函数贝塞尔提取中，其基函数可表示为

(15)

式中：we为单元的权系数矢量；We为单元权系数的对角矩阵.

1.3 HB样条构造

为解决张量积B样条局部细化问题，本小节给出HB样条基函数构造方式.

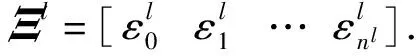
HB样条基函数包含有各个细分层的B样条基函数，它是一组函数N=∪lNl作为分析和几何描述的基函数.HB样条基函数的构造从一个定义在区域Ω0的NURBS基函数N0上展开的.HB样条的基函数K通过下面的递推公式给出.

① 初始：K0={τ∈N0:suppτ≠∅}.

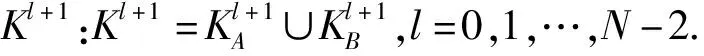
③K=KN-1.

1.4 多层贝塞尔提取

为了实现HB样条贝塞尔提取，首先定义相邻两层间基函数关系.基于节点插入算法，第l层的B样条基Nl都可以表示成细化的第l+1层的B样条基Nl+1的线性组合为

Nl=Ml,l+1Nl+1,

(16)

式中M为细分算子[13-14].因此，相邻连续层之间的控制点的关系为

(17)

上述细化算法可保持几何构型不变.两个不连续层I,J(J>I)之间的细分算子可由相邻细分算子连乘得到

(18)

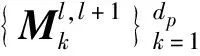
(19)

通过细分算子建立各个细分层基函数之间的关系.

其次，对于HB样条基函数的贝塞尔提取算子，由于HB样条的基函数包含有各个不同细分层的基函数，每个HB样条的单元的形函数包括多层B样条基函数.将单元ε′ei(第l层的第ei个单元)的形函数统一用该单元所在层l的B样条基函数Nl表示.在第l层进行贝塞尔提取，从而得到多层贝塞尔提取.下面通过一个例子，如图5所示，具体说明多层贝塞尔提取算子构造过程.

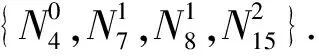
(20)

式中MLε3称为多层细分算子，它是通过组合多个细分算子的行向量来推导得到.例如，单元的多层细分算子是通过组合R0,2，R1,2和R2,2中相应的行向量得到.通过多层细分算子，则层次B样条的基函数可以表示成单一层标准B样条的基函数.将第2层的B样条基函数通过贝塞尔提取，表示成伯恩斯坦基函数的组合，

(21)

式中Cε5为单元的贝塞尔提取算子.最后，单元ε5的形函数就表示为伯恩斯坦基函数的线性组合，

(22)

式中MLε5Cε5称为多层贝塞尔提取算子[12].

由此，对于HB样条基函数，采用伯恩斯坦基函数来表示，实现单元形函数统一化，有效地简化等几何分析程序，更加方便地与传统有限元程序相融合.

2 大变形平面结构动力学建模方法

2.1 大变形平面等几何有限单元

基于等几何分析方法，采用HB样条基函数描述弹性体构型，并通过连续介质力理论描述弹性体的变形，从而建立平面板结构的动力学模型.平面单元在发生大变形后，其变形后的构型为当前构型，初始构型为参考构型，单元的参数域单元可视为母单元构型，它们之间的关系如图6所示.

考虑任意平面板结构，其初始几何构型通过NURBS曲面描述.以NURBS曲面片中的一个单元[ξi,ξi+1]×[ηj,ηj+1]为研究对象.在发生大转动大变形后其上任意一点P的位置坐标可表示为

r(ξ,η,t)=r0(ξ,η)+u(ξ,η,t)=S(ξ,η)e(t),

(23)

式中：u(ξ,η,t)为点P的位移，S(ξ,η)为NURBS基函数在定义域[ξi,ξi+1]×[ηj,ηj+1]内的非零元素，也就是单元的形函数，e(t)为NURBS单元控制点，称为单元广义坐标.为了提高计算效率，对公式(23)中的单元广义坐标进行重排，点P的位置坐标可重新表示为[15]

(24)

⋮ ⋮

(25)

基于连续介质力学理论，平面等几何单元的变形梯度张量F可表示为

(26)

(27)

其中，i=1,2,,2×[(p+1)×(q+1)]，m=1,2,a=1,2,n=1,2，单元弹性力可表示为应变能对广义坐标的1次偏导数，

(28)

式中D为4阶弹性张量.将式(27)带入式(28)，则弹性力的分量可进一步表示为

(29)

2.2 大变形结构动力学方程时间积分算法

对于动力学系统而言，动力学方程可由第一类拉格朗日方程得出：

(30)

式中：M为系统质量阵；q为系统广义坐标；F为系统弹性力；Q为系统广义外力；Φ和Φq分别为系统约束方程以及对广义坐标的雅克比矩阵；λ为拉格朗日乘子.

动力学方程的求解采用广义-α方法[16].动力学方程进行时间离散后，需在在每个时间步长内通过Newton-Raphson迭代求解方程组：

(31)

式中Δq和Δλ是广义坐标和拉格朗日乘子的增量，

(32)

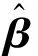
2.3 SPR误差估计方法

在等几何分析中，将HB样条基函数作为几何离散和分析求解的基函数，可实现网格的局部细化.在实际计算中，对于一个求解模型，需要确定具体的细分区域.例如，对于具有孔结构的模型，其孔周应力集中，位移梯度变化较大，需要在孔周区域建立多个细分层.对于复杂结构，加密区域无法事先获得，而为了实现自适应细化，误差估计算法是其中的一个重要环节.

等几何分析的能量范数误差定义为

(33)

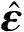
Δi/Δ>const,

(34)

其中，参数const是一个常量，则该单元的误差较大，需要进一步细化.

通常，大变形结构动力学问题无法获取解析解，可采用超收敛修复方法(superconvergence patch recovery，SPR)修复应力，可得到应力的参考解.SPR将高斯点上的应力值映射至控制点上，可得到整个单元修复应力场，从而可获得整体修复应力场.将该修复的应力场当作参考解，从而可获得系统的应力误差或能量误差.

通常情况下，数值求解之后，仅可获得高斯点处的应力值，即应力场的强形式为

(35)

将式(35)进行变分，同时在单元内或整个求解域积分，可得到对应的弱形式为

(36)

离散后进行高斯积分后可表示为

∑wNTNTnode=∑wNTTGauss,

(37)

因此，节点的应力值可表示为

Tnode=Ψ/PGauss,

(38)

式中：Ψ=∑wNTN，PGauss=∑wNT，N为单元的形函数；w为高斯积分系数.

求解域的应力场可通过B样条基函数插值得到：T(ξ,η)=S(ξ,η)Tnode，将该修复应力场当作视为应力参考解，可获得系统的能量范数误差.

3 数值算例

3.1 圆孔线弹性问题

第一个算例是一个无限大平板的孔周应力集中问题.本文研究了在平面应力假设下的线弹性问题：

divσ(u)=f,

(39)

由于对称性，计算域选取1/4区域，如图7所示，该算例的仿真参数来源于文献[8]中的第4.2小节.该静力学问题的解析解为

(40)

采用NURBS样条基函数作为几何离散的基函数，能够精确描述圆孔构型.层次细化是一个保证几何不变的过程，通过简单的节点插入算法就可以计算出NURBS样条的新的权系数和控制点.初始构型采用2阶NURBS样条描述，初始广义坐标个数是28，网格数是8，最终通过3次网格局部层次细化产生了一个4层自适应网格，如图8所示.

3.2 平面板的结构动力学问题

本算例研究一大变形平面板的结构动力学问题.一个矩形板在重力作用下振动，板的左端固支，如图10所示，板的长度宽度以及厚度分别是2，1和1 m，密度是7 810 kg/m3，弹性模量10 MPa，泊松比0.3.仿真计算时间是2 s，时间积分步长是10-4s.

平面板结构的初始构型采用2阶NURBS样条描述，初始网格数是32，初始广义坐标个数是60，在进行网格自适应细化的过程中，采用HB样条的网格细分方法，通过SPR方法修复应力，得到能量范数误差来指导自适应过程.在平面板的振动过程中，在误差较大的区域进行网格细化，共进行了3次网格细化，最后形成了4层HB样条细分网格，最终网格数是368，初始广义坐标个数是420.图11是该结构不同细化程度的网格图，1/8左边界部分最终网格最密集.参考模型也采用NURBS样条来建模计算求解，其网格数和初始广义坐标个数分别为368、450，它与求解模型中最密网格数和初始广义坐标个数基本一致.图12给出了整个计算过程中系统的能量范数误差，相同初始广义坐标个数时，均匀网格的参考模型的误差峰值为12.33，而采用HB样条建模计算的误差峰值为9.20，减小了25.4%.图13表示1/8左边界区域能量范数误差，该部分是误差较大区域，从图中可看出，误差峰值从均匀网格的9.32减小到6.59，降低了35.5%，平均误差从4.37减小到3.10，降低了29.0%.由此说明基于HB样条能够有效地提高大变形平面结构动力学问题的计算效率与精度.