基于k-目标跟踪的节点部署优化算法
2020-07-15白秋产张昊伦
白秋产,张昊伦
(1.淮阴工学院 自动化学院,江苏 淮安 223003;2. 黑龙江大学 机电工程学院, 黑龙江 哈尔滨 150080)
0 引 言
无线传感网络(WSNs)已广泛应用于机器人系统、病人看护、目标跟踪[1-2].在目标跟踪应用中,先将传感节点部署于兴趣区域[3-4],再通过这些传感节点感测目标移动,进而实现对目标的跟踪.WSNs中的目标跟踪被认为是衡量跟踪系统(TTS)[5-8]的跟踪性能的重要指标.
若有k个定向节点同时跟踪FoI的移动目标,则称为k-目标跟踪(kTT).图1示出了一个TTS系统,传感节点分布于长形区域,目标在FoI内移动.当靠近移动目标时,定向节点就将跟踪信息传输至信宿.如果从定向节点至信宿有m条连通路径,且m≥1,则称为m-连通.
本文旨在通过优化节点部署方案,提高WSNs内的kTT的跟踪质量.考虑三角形、矩形和六边形节点部署模型,并针对这些模型解决问题:如何以最少的节点实现目标跟踪.文献[9]利用超宽带传感节点和Bernoulli滤波器解决目标跟踪问题[10].通过Bernoulli滤除数据噪声.类似地,文献[11]针对1-覆盖和m-连通的WSNs,研究了最优节点部署策略.此外,文献[12]也研究了节点部署问题.依据不同的通信半径和感测半径,研究如何以最少的节点数实现4-连通和兴趣区域的全覆盖.

图1 TTS的示例
然而,现在的解决目标跟踪问题方案仅考虑一个目标跟踪.并且,这些节点部署方案只是基于特定的区域.为此,针对目标跟踪问题进行分析.考虑三种规则形状(等边三角形、矩形和六边形),分析在这些规则形状下实现k-目标跟踪所需的节点数,并推导了最优边长.
1 系统模型及约束条件
定向节点确定性地部署在兴趣区域Ψ内.考虑三种规则多边形:等边三角形、矩形和六边形,如图2所示.图2中的点a和点b表示一段路线的始点和终点.
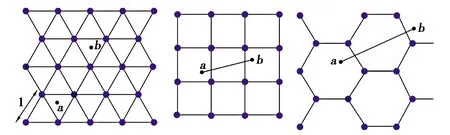
(a)等边三角形 (b)矩形 (c)六边形
令l表示多边形的边长,且l>0.并引用p表示多边形,p=0、1、2分别表示等边三角形、矩形、六边形.同时,令(x,y)表示FoI内的节点位置,且(x,y)∈Ψ,x≥0,y≥0.
1.1 跟踪模型
引用定向的跟踪模型[13].图3示出了一个定向节点模型.令φ表示节点的跟踪角度,且1≤φ≤360°.此外,每个节点只有有限的跟踪半径.令Rs表示节点的跟踪半径,且Rs>0.
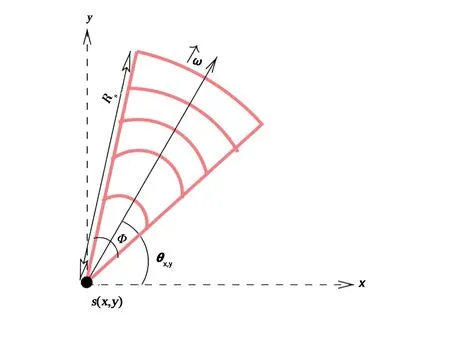
图3 定向节点模型
引用跟踪区域的定向(OTR)变量,其表示FoI内定向节点的方向.令θx,y表示将位于s(x,y)处的节点的定向矢量,且0≤θx,y≤2π.
1.2 通信模型
引用全向的通信模型.节点si能够与其通信范围Rc内的任何节点通信.令A(si,Rc)表示节点si的通信区域.假定网络内所有节点具有相同的通信半径Rc.
定义1:如果节点si离节点sj的距离小于Rc,则节点sj就是节点si的一个邻居节点.在m-连通的WSNs,任意节点sx的邻居节点数大于m,且m≥1.
定义2:令点a和点b是路径一段的始点和终点.这两点的欧式距离就是该段的长度,如图2所示.令l表示规则多边形的边长.若满足式(1),则表明目标穿越了至少一个跟踪区域,即
Lsegment≥lp+1.
(1)
1.3 目标跟踪问题
给定FoI区域Ψ的参数(Rs、Rc、k、m、Lsegment),目标跟踪问题就是:决定区域Ψ内定向节点的位置和跟踪区域OTR,致使移动目标至少被k个定向节点跟踪,且所需的定向节点数最少.
2 目标跟踪问题的解
本节针对三个不同模型(等边三角形、矩形和六边形),求解目标跟踪问题.求解过程可分为4个阶段.第一步,估计定向节点坐标;第二步,估计跟踪区域的OTR,随后再针对给定模型,估计最优的边长度(OSL),最后,再依据OSL和规则模型计算所需的最少节点数.
2.1 节点坐标
针对等边三角形、矩形和六边形模型,求解目标跟踪问题.最初,将FoI划分为规则形状,然后再计算节点坐标.如图4所示.
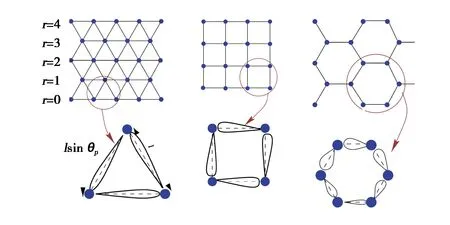
(a)等边三角形 (b)矩形 (c)六边形
令l表示边长,lp表示高度,且lp=lsinθp,其中p=0,1,2.将FoI区域划分偶数和奇数行,并令r表示行数.
在偶数行里,即r=(0,2,4,…),用行数r表示节点的横坐标(x)和纵坐标(y),即x=rl、y=rlp.类似地,在奇数行,即r=(1,3,5,…)时,横坐标x在rl的基础上加l/2.因此,用式(2)表示节点坐标.
(x,y)∈{(rl,rlp),r=(0,2,4,…),
(rl+l/2,rlp),r=(1,3,5,…).
(2)
在矩形模型中,如图4(b)所示, 横坐标和纵坐标相等.因此,可用式(3)计算矩形模型的节点坐标:
(x,y)∈(rl,rlp).
(3)
三角形与六边形模型的差别仅在于:节点是否位于六边形的中心,如图4(c)所示.为了估计六边形模型中节点坐标,就依据式(2)判断是否节点位于六边形内,如满足:mod(y/lp,2)=mod(x,3)+1,则表明六边形内没有节点.
2.2OTR
使用以下定理推导每个模型中节点的OTR.
定理1:将兴趣区域Ψ划分等边长l的矩形.令θx,y表示位于(x,y)处节点的方向,其中{x,y}≥0.如果满足式(4),则兴趣区域就能被k-目标跟踪.
Rs≥2klandθx,y=mod(x+y,2)×π2.
(4)
定理2:将兴趣区域Ψ划分等边三角形,且边长为l.令θx,y表示位于(x,y)处节点的方向,如果满足式(5),则兴趣区域就能被k-目标跟踪:
Rs≥3klandθx,y=mod((x+y+
mod(y,2)),3)×π3.
(5)
定理3:将兴趣区域Ψ划分六边形,且边长为l.令θx,y表示位于(x,y)处节点的方向,如果满足式(6),则兴趣区域就能被k-目标跟跟踪:
Rs≥4klandθx,y=mod((x+y+mod(y,2)),3)×π3.
(6)
结合式(4)、(5)和(6),将OTR综述地表述如下:将兴趣区域Ψ划分模型p,且边长为l,则兴趣区域就能被k-目标跟跟踪的条件:
Rs≥(3p2-5p+62)kl,
(7)
且
θx,y≥
{mod((x+y+mod(y,2)),3)×θ0,ifp=0,
mod((x+y),2)×θ0,ifp=1,
mod((x+y+mod(y,2)),3)×θ0,ifp=2.
(8)
2.3OSL
令s(x,y)表示节点s的位置.令离节点s最近的第m个邻居节点位于υ.将节点s离此邻居节点的距离表示为dp,m.
min(Lsegmentp+1,2Rs(3p2-5p+6)k,Rcdp,m).
(9)
2.4 节点的部署
利用OSL在兴趣区域Ψ部署节点.假定在宽为L、长为B的规则区域内,所需的节点数Np.
Np=(Lsegmentsinθp)
(Bsegment-Bpcosθp3segment-cosθp).
(10)
式中,p=0,1,2.
先计算三种形状(等边三角形、矩形、六边形)下所需的节点数的最小值Nmin,并记录Nmin值所对应的形状(即p值).为了简化描述,用p*表示能获取最小Np值所对应的p值.
Nmin={Np*|minp=0,1,2Np}.
(11)
将p*也称为最优模型.再将p*代入式(9),得到最优的OSL值*segment.将p*赋给p(p←p*)、*segment赋给l(l←*segment).然后,依据式(12)计算节点s(x,y)的位置:
(rl+lcos(θp2)cos(θp)mod(ylp,2),rlp).
(12)
如果(x,y)位于Ψ内,且将节点放置于s(x,y)处.若不属于Ψ内,就将节点放置在Ψ边界上交叉点上.对将x、y的进行更新:
x←x+l、y←y+lp,
(13)
如图5显示部署节点过程.

图5 部署节点的过程
3 性能仿真
3.1 仿真参数
利用NS 2.34软件建立仿真平台.具体的仿真参数如表1所示.考虑两个目标移动模型:1)随机步行移动 (RKM)模型;2)随机航点移动(RPM)模型.

表1 仿真参数
在RKM模型中,目标随机选择移动方向和移动速度,从当前位置移动至另一个位置.速度范围限定在[ϑmin,ϑmax],方向限定在[0,2π].令ϑavg表示目标的平均移动速度.在固定时间间隔Ct或者移动固定距离Cd后完成目标移动.而RPM模型中,目标每移动一段时间就暂停一段时间Pt.然后,再随机选择目的节点,以平均速度ϑavg进行移动.
3.2 跟踪角的影响
首先分析跟踪角对跟踪误差的影响.跟踪误差是指目标准确的位置与所跟踪的位置间差值.表2~7示出了在等边三角形、矩形和六边形模型中的跟踪误差.

表2 RKM条件下跟踪误差(等边三角形)
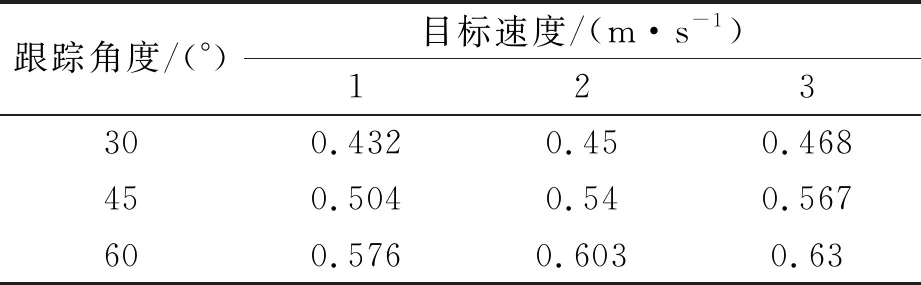
表3 RPM条件下跟踪误差(等边三角形)
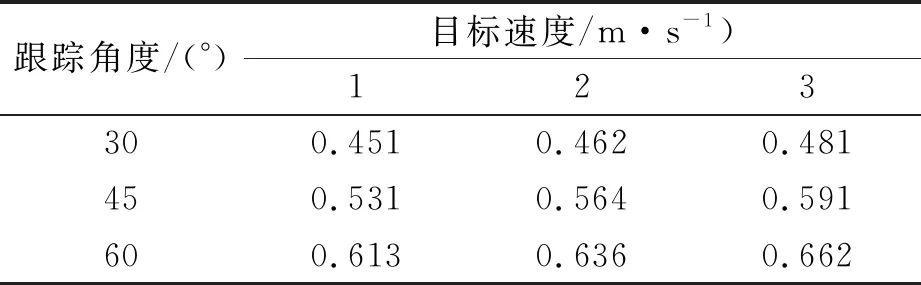
表4 RKM条件下跟踪误差(矩形)
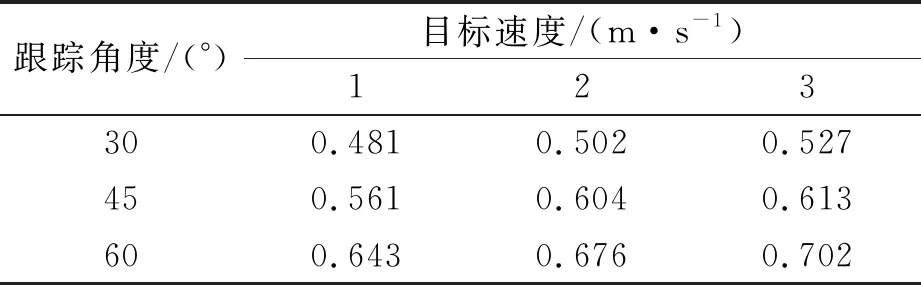
表5 RPM条件下跟踪误差(矩形)

表6 RKM条件下跟踪误差(六边形)

表7 RPM条件下跟踪误差(六边形)
从表2~7可知,目标的角度和速度的增加,增加了跟踪误差.原因在于:速度的增加,降低了目标的稳定性.此外,相比于矩形和六边形,等边三角形具有最小的平均跟踪误差.
3.3 跟踪距离的影响
表8~13示出了跟踪距离对跟踪误差的影响.从表中的数据可知,当跟踪距离从5 m增加至10 m时,平均跟踪误差提高了近50%.原因在于:跟踪距离越大,用于跟踪的信号强度就越弱.这不利于跟踪精度.

表8 RKM条件下跟踪误差(等边三角形)

表9 RPM条件下跟踪误差(等边三角形)

表10 RKM条件下跟踪误差(矩形)

表11 RPM条件下跟踪误差(矩形)
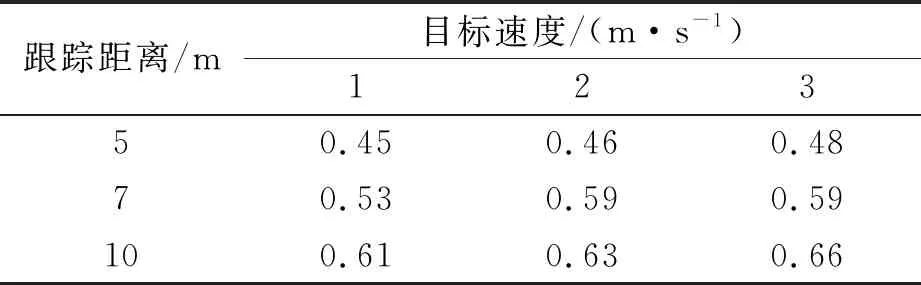
表12 RKM条件下跟踪误差(六边形)

表13 RPM条件下跟踪误差(六边形)
3.4 目标跟踪k值的影响
本小节分析k值对目标跟踪性能的影响.首先考虑k值对所需的节点数Np的影响.仿真参数:m=1、Rc=45 m、Rs=35 m、‖Ψ‖=200 m×200 m,l=8 m.仿真数据如图6所示.
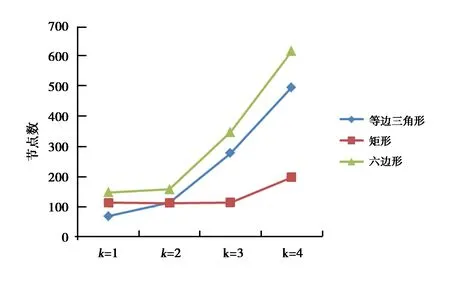
图6 所需的节点数
由图6可知,符合预期,k值的增加,增加了所需的节点数.此外,除了k=1外,矩形模型所需的节点数最少.原因在于:k值越高,跟踪重叠区域越多,这就增加所需的节点数.
然后,考虑k值对节点的跟踪距离范围的影响.仿真参数:m=1、Rs=45 m、‖Ψ‖=200 m×200 m,l=8 m,Np=200.仿真数据如图7所示.

图7 跟踪距离范围
由图7可知,节点的跟踪距离范围随k值增加而上升.原因在于:在固定的节点数和跟踪角度前提下,k值越大,跟踪的区域就越大.
4 总 结
针对WSNs中k-目标跟踪问题,进行分析,并利用定向节点解决k-目标跟踪问题.基于规则形状,推导了最优边长和所需的节点数,并优化部署节点,进而解决目标跟踪问题.最终,通过数值证实分析的正确性.本文的分析给设计基于WSNs的目标跟踪的节点部署提供参考.
