MADOCA-LEX高频GPS卫星钟差短期预测精度分析

虢盛,张绍成,李玮,独士康

(中国地质大学(武汉) 地理与信息工程学院,湖北 武汉 430078)

关键字: 全球定位系统;卫星钟差;阿伦方差;稳定性分析;钟差预报

0 引 言

卫星钟的稳定性是影响全球卫星导航系统(GNSS)导航定位精度的重要因素[1]．国际GNSS服务组织(IGS)提供采样率为30 s和5 min的GPS精密钟差,但其较低的采样频率和产品时延无法满足实时高频高精度用户的需求[2]．日本准天顶卫星系统(QZSS)作为一个区域性卫星导航系统,除播发与GNSS相同的导航定位信号外,还通过卫星频段播发采样率为1 s的精密钟差和采样率为30 s的精密轨道产品[3],使得能够消除在分析卫星钟稳定性时使用较低频采样率数据内插高频数据引起的粗差[4]．日本宇宙航空研究开发机构(JAXA)提供的精密轨道和钟差产品是MADOCA (Multi-GNSS Advanced Demonstration tool for Orbit and Clock Analysis)数据处理软件生成,并通过L频段1278.75 MHz的实验频率播发给地面用户,因而也被称为MADOCA-LEX(L-band Experiment)产品[5]．

国内外学者已就GNSS卫星钟差的中长期稳定性和预报技术进行了较多的研究：文献[6]基于IGS提供的采样率为30 s的钟差产品对卫星钟的中长期稳定性进行了分析[6],文献[7]采用灰色模型对6 h的钟差进行了中长期预报和最优预报模型的探究[7]．这些研究主要针对卫星钟在与地面监测站失联后,仅靠自身维持与系统时间同步时所做的中长期预报,文献[8-9]揭示了其普遍精度一般在纳秒级别,主要用于数米精度的导航应用．JAXA发布的MADOCA-LEX产品提供了0.1 ns精度的钟差,但实时播发中可能存在6～8 s的时延[5],在用户使用过程中钟差对测距精度的影响会进一步增加．因此需要分析卫星钟差在数秒内的短期稳定性,评估实时钟差在数秒时延条件下的精度．

本文首先对MADOCA-LEX产品及特性进行简要介绍,然后介绍了卫星钟差稳定性分析和预报的方法,最后基于MADOCA-LEX提供的高频GPS钟差数据和阿伦方差对卫星钟短期稳定性进行分析,并采用多项式模型和灰色模型进行短期钟差预报,评价模型对不同类型GPS卫星钟差预报的精度．

1 MADOCA-LEX产品

日本准天顶系统(QZSS)是由日本宇宙航空开发机构(JAXA)运营,自2017年2月28日起由日本内阁府(CAO)控制QZS-1覆盖整个亚洲-大洋洲的区域性卫星导航系统．2018年11月1日,日本官方宣布QZSS开始正式提供LEX增强服务[10]．为满足GNSS用户实时精密单点定位(PPP)等高频高动态应用的需求,JAXA基于MADOCA软件平台实时收集处理全球52个GNSS系统监测站的观测数据,解算GNSS卫星的高频轨道参数和卫星钟差,并通过互联网或QZSS卫星的导航频段实时播发给地面接收机,为用户提供不需要外部互联网连接的实时PPP服务．

若用户需要对产品质量进行分析,可以从JAXA的FTP服务器上下载包括 RTCM10403.2-SSR (ssrXXXXX.rtcm)、RINEX SP3(madocaXXXXX.sp3)格式的MADOCA产品(ftp://mgmds01.tksc.jaxa.jp/)．本文所用1 s采样率的MADOCA实时钟差改正产品格式为RTCM-SSR,电文类型为1058,实时GPS精密钟差产品是通过广播星历计算的卫星钟差和 MADOCA 实时钟差改正产品恢复得到．

MADOCA-LEX产品的数据主要包括轨道、时钟、差分码偏差和用户测距精度(URA)等信息,其中卫星轨道数据每30 s更新一次;钟差数据每1 s更新一次,延迟一般为6～8 s;而URA则用于评估GPS、GLONASS、Galileo和QZSS的距离精度,每30 s更新一次;差分码偏差的更新周期为1 d．该产品GPS卫星钟差的目标精度为0.1 ns,实时定位误差小于10 cm[5]．国内外学者已从该产品的钟差精度[11]、可用性[10]和在PPP领域的应用[12]等多方面对MADOCA-LEX产品进行了分析,证实了该产品的定位服务精度能够达到厘米级PPP应用的需求．

2 钟差稳定性分析及预报模型

2.1 数据预处理方法

星载原子钟在轨期间,因硬件故障或外界环境等因素,原始钟差数据中不可避免地会出现粗差．为消除粗差数据对评估结果的影响,需对原始钟差数据进行数据预处理[1]．数据预处理前,通常需要先将原始钟差转化为频率数据．转换公式为

(1)

式中:xi为i时刻钟差数据;fi为频率数据．考虑到较长时间的钟差频率数据的数据量较大,为提高效率,本文使用中位数法对粗差数据进行剔除,具体公式如下[13]:

MAD=Median{|yi-m|/0.6745},

(2)

式中,m=Median{yi},当观测量|yi|>(m+n·MAD)时,将其标为粗差点,本文仅对数据进行n=3的粗差剔除的预处理操作．

2.2 基于阿伦方差的稳定性分析

GPS星载原子钟主要有铷钟和铯钟两种,其中铯钟频标输出频率频漂接近于0,常使用阿伦方差[14]进行稳定度分析;而铷钟长期频漂较为明显,一般采用哈达玛方差[6]进行稳定度分析．但考虑到铷钟短期内频漂并不十分明显[15],为保证各原子钟稳定性分析方法的一致性,本文统一使用阿伦方差对卫星钟稳定性进行分析,其公式表达如下:

(3)

2.3 参数估计模型

2.3.1 多项式模型(PM)

PM是短期钟差拟合预报中应用最广泛的模型之一,能够较好地表征卫星钟时频特性,常应用于GNSS实时导航定位等应用的钟差预报[1]．常用的多项式模型主要包括一阶模型(LM)[16]、二阶模型(QP)[17]和高阶多项式模型．数学表达式如下:

xi=a0+a1(ti-t0)+a2(ti-t0)2+…+

(4)

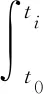
2.3.2 灰色模型(GM)

对于采样间隔均匀的钟差时间序列,可利用灰色模型进行建模和预报,其模型公式可表达如下[18]:

(5)

式中：x(0)(k)表示钟差原始序列中的第k个数据,k=1,2,…,n;a、u为待确定参数,其值可以通过对样本或样本的衍生数列采用最小二乘准则求得．灰色模型的优点是只需要少量的已知数据就能建立模型;缺点是无法充分利用更多的已有数据来提高其预报精度．本文预报钟差所用时间序列数据最少为5个,最多仅有30个,灰色模型具备可行性．

3 数据分析

3.1 算例数据

本文采用2020年1月1日-21日连续21天的1 s钟差数据(MADOCA服务器1月24-28日处于维护状态,数据产品中断服务),对所有在轨GPS卫星钟性能进行评估．由于MADOCA-LEX产品暂无最新的Block ⅢA卫星的钟差产品,因而本文无法对最新的G04、G18卫星钟差进行评估．为便于比较分析,将本文涉及的所有卫星分类列举如表1所示.

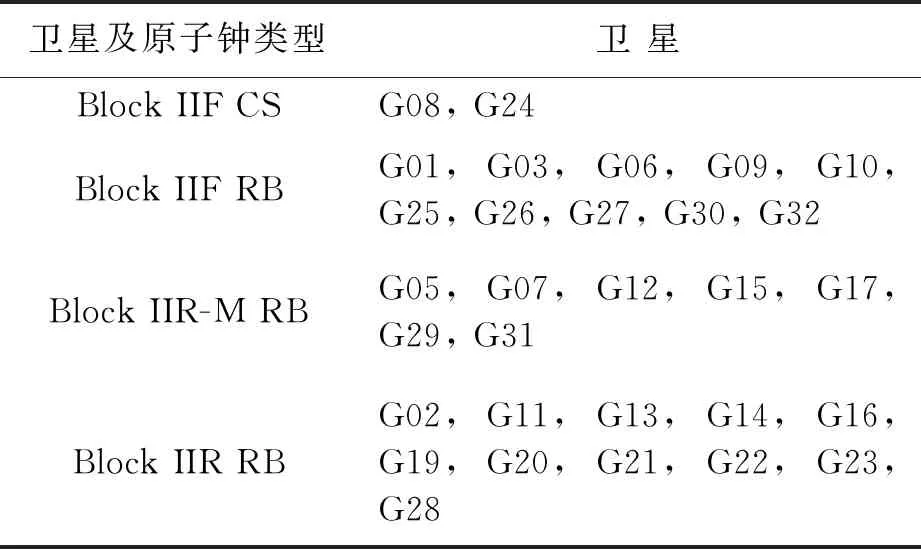
表1 本文涉及GPS卫星及原子钟类型分类

3.2 稳定性分析

使用2020年1月1日-21日的数据,采用阿伦方差画出原子钟在[1,5,10,50,100,200,300,400,1000]s的稳定性结果如图1所示．由图可知,几种不同类型卫星钟差的10 s稳定性均在10-12s量级且5 s以内稳定性无明显差异;就5 s以上的稳定性而言，配备铷钟的Block IIF卫星钟差稳定性的优势逐渐体现,百秒稳在10-12到10-13量级,而配备铯钟的Block IIF卫星钟差稳定性略差于其他卫星．Block ⅡR-M钟与Block ⅡR钟差稳定特性整体上无明显差异,千秒稳在10-13s,相较于Block IIF铷钟而言,该钟稳定性一致性要略微分散．图1中体现的各种卫星100 s以上稳定特性与使用IGS中心提供的采样率为30 s的数据分析的GPS卫星钟稳定性的结论一致[19]．由于本文考虑的是实时PPP中,高频钟差在6～8 s的数据延迟情况下所存在的精度损失,因此主要关注原子钟5～10 s时间间隔的稳定特性．

图1 不同类型GPS卫星高频钟差稳定性

为验证各种卫星钟差多天的短期钟差稳定性,本文以G08(Block ⅡF铯钟)，G15(Block ⅡR-M 铷钟),G21(Block ⅡR铷钟),和 G32(Block ⅡF 铷钟)4颗典型卫星为例,其2020年1月1日-21日连续21天的10 s稳定性对比如图2所示:4种不同类型卫星钟差的10 s稳定性都在10-12量级,且绝对数值无明显变化,验证了本文的钟差产品稳定性分析的可靠性．

图2 四颗典型GPS卫星单天钟差的10 s稳定性

3.3 短期钟差预报

分别使用LM、QP和GM对GPS卫星钟差进行建模预报,评估不同拟合窗口长度对钟差预报精度的影响．选取JAXA数据中心提供的2020年1月1日一整天的采样间隔为1 s的实时精密钟差数据,将全天86 400个历元分别按照5 s,10 s和30 s间隔分为若干组,每组数据均采用LM、QP和GM建立钟差预报模型并预测后续10 s时长的钟差,然后以MADOCA-LEX提供的后续实际钟差为参考值,评价预报钟差的精度．本文选用预报残差的均方误差(RMS)作为衡量钟差预报精度的指标,来比较不同模型和拟合窗口长度的精度差异．

首先使用5 s拟合窗口,分别采用LM、QP和GM模型建模,预报残差的RMS值随预报时长的变化趋势如图3所示:三种模型的预报精度都随着预报时长增加而降低,且铯钟精度随时间衰减最为显著,其中LM模型预报残差的RMS值均在0.1 ns以内,GM模型的精度稍差,RMS值最大达到0.15 ns．QP模型预报精度较低,10 s后RMS值可达0.4 ns,此偏差折合测距误差达到12 cm,无法保证厘米级的定位精度．

图3 5 s拟合窗口长度10 s钟差预报残差RMS对比

将拟合窗口增加到10 s后,预报精度如图4所示:三种模型的预测精度与使用5 s时长时基本一致,其中LM模型预报精度仍为最佳,RMS小于0.1 ns,QP模型的预报精度有较大提高,其RMS值大多低于0.2 ns,而GM预测模型则有两颗RMS值接近0.2 ns的Block-IIR 铷钟,预报精度较差,稳定性还有待提高．

图4 10 s拟合窗口长度10 s钟差预报残差RMS对比

拟合窗口再次增加至30 s时长的钟差预报精度如图5所示:QP模型的预报精度显著提高,所有卫星的RMS值均低于0.1 ns．LM模型因未考虑钟的频漂特性,预报精度明显退化,误差可达0.4 ns;该现象在GM预报模型中体现得更为明显,除两颗精度明显发散的Block IIR卫星以外,其他卫星预报钟差的RMS值也接近0.5 ns．因此,使用30 s拟合时长进行钟差预报时,QP模型精度要高于LM和GM模型．

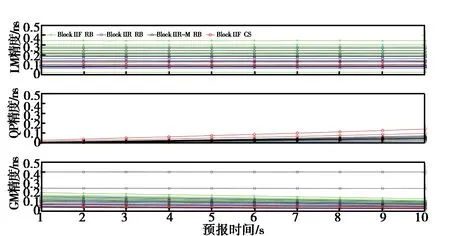
图5 30 s拟合窗口长度10 s钟差预报残差RMS对比

上述基于不同种类卫星钟差的短期预报对比结果可见,加载铷钟的卫星钟差预报精度整体略高于Block IIF铯钟,与图1钟铷钟10 s短期稳定性高于铯钟一致．采用5 s和10 s拟合窗口时,一阶线性模型即可得到较好钟差预报精度,延迟10 s之后其预报精度仍然不超过0.1 ns．如采用30 s拟合窗口,则需要考虑卫星钟的频漂特性,因此采用QP预报精度更优,达到0.15 ns以内．灰色预报模型常见于钟差产品的长期预报,本文的3种拟合窗口长度下短期钟差预报中未体现优势,不建议用于钟差短期预报．

4 结束语

本文基于MADOCA-LEX产品提供的1 s采样率的GPS精密钟差,首先用阿伦方差分析各卫星原子钟的短期稳定性,并用多天的数据比较不同类型GPS卫星钟的多天10 s稳定性．然后分别使用LM、QP和GM对原子钟10 s内的钟差进行了预报和精度评估．分析结果显示:

1)MADOCA-LEX提供的高频钟差产品5 s和10 s稳定性都达到了10-12量级,数据产品10 s以内漂移理论上不会超过0.1 ns;

2)采用5 s或10 s拟合时长窗口进行钟差预报时,因卫星钟差的频漂都不明显,LM模型相对于QP和GM模型而言预测精度最高且效果最为稳定;若采用30 s时长的窗口进行钟差预报,QP模型因考虑了卫星钟的频漂效应,预测效果更为可靠．两种模式的钟差预测残差RMS值都可达到0.15 ns以内,满足厘米级PPP的需求．