大电网可靠性中的故障限流器优化配置研究

章勇高　李小蓓　方华亮　龚俊

摘 要：针对特高压（UHV）工程接入使得电网规模不断扩大、短路电流水平持续升高，导致电网安全稳定运行隐患变大的问题，提出一種基于电网可靠性的限流器优化配置方法。通过短路计算，量化评估电网的可靠性，实现短路影响下的可靠性分析。建立可靠性评估与短路电流、负荷损失量之间的量化模型，根据可靠性量化结果，确定限流器的候选安装点。采用粒子群优化算法，以电网短路下可靠性水平、限流器数量最少为目标，对限流器的布点进行优化。最后以某省实际电网为例，结果表明，这一方法可缩小最优解的搜索空间，实现限流器的优化配置，并有效地限制短路电流，提高电网运行可靠性。

关键词：短路电流;可靠性;故障限流器;优化配置;粒子群优化算法;特高压

DOI：10.15938/j.emc.2020.06.010

中图分类号：TM 713文献标志码：A 文章编号：1007-449X（2020）06-0081-09

Optimal configuration of fault current limiter in large power network

ZHANG Yong-gao1， LI Xiao-bei1， FANG Hua-liang2， GONG Jun2

（1.School of Electrical and Automation Engineering， East China Jiaotong University， Nanchang 330013， China;2.School of Electrical Engineering， Wuhan University， Wuhan 430072，China）

Abstract：Ultra-high voltage（UHV） project access makes the scale of power grid expand continuously， and the level of short-circuit current continues to rise， which leads to the greater hidden danger of safe and stable operation of power grid. To solve this problem， a method of optimal configuration of current limiter based on power grid reliability is proposed.Through short circuit calculation， the reliability of power grid was evaluated quantitatively， and the reliability analysis under the influence of short circuit was realized.The quantitative model between reliability evaluation and short-circuit current as well as load loss was established. According to the quantitative results of reliability， the candidate installation points of current limiter were determined.Particle swarm optimization algorithm was used to optimize the distribution of current limiters， aiming at the reliability level and the minimum number of current limiters under short circuit. Finally， taking the actual power grid of some province as an example， the results show that this method reduces the search space of the optimal solution， realizes the optimal configuration of current limiter， and effectively limits the short-circuit current. It is proved to improve the reliability of power grid operation.

Keywords：short circuit current; reliability;fault current limiter;configuration optimization;particle swarm optimization algorithm; ultra-high voltage

0 引 言

随着我国电网的不断发展，电网规模不断扩大，逐步形成以特高压（ultra high voltage，UHV）为主干网架的电力网络。特高压电网规模大、传输距离远、传送容量大，导致特高压接入后电网的短路电流水平快速升高，影响面广。因此，短路电流超标直接影响了特高压电网安全稳定运行，成为特高压发展中急需解决的问题之一。

目前，针对电网短路电流越限问题，已提出多种限流措施，主要分为2种：一种是通过调整电网结构，改变系统运行方式;文献[1-3]在基于转移阻抗灵敏度加权和适应函数的基础上提出线路开断网架调整数学模型，形成一种快速计算网架调整全局优化算法进而限制短路电流;另一种是通过加装限流器方式实现对短路电流的控制。文献[4-5]以网损及经济成本为目标函数建立模型，实现限流器的优化配置。文献[6-8]以短路电流及支路阻抗灵敏度变化为基础建立模型，结合算法进行限流器的优化布点。文献[9]提出以加装电抗器的数量和总阻抗值最小为优化目标，采用粒子群算法进行优化布点的模型。

上述算法模型主要在加装限流器前后的阻抗变化上进行考虑，虽然也能够有效缩小优化搜索范围，但在实际大电网中线路较多時搜索效率较低。其次，已有的研究主要是针对限流的分析模型、灵敏度、损耗及经济性等问题进行深入分析，而目前限流措施针对电网中所有设备可靠性水平较高时，可实现较好的限流效果，但在实际电网运行中，各个设备的可靠性水平不一样。本文提出考虑可靠性的限流分析是对当前研究的有效补充，从另一个角度保证短路后电网安全稳定运行。

可靠性是电网运行的首要前提，发生短路时首先要保证电网运行的动态可靠性。发生短路后电流急剧上升，电网中可靠性水平较低的设备也可能引发新的故障，使得故障进一步扩散，最终造成连锁故障。因此，短路情况下电网动态可靠性评估十分重要，而目前短路限流方案中没有考虑电网在安装限流器前后的可靠性问题。其次，对于限流器的优化安装，以上模型虽对限流器进行布点配置，但对于其安装后能否稳定可靠的运行存在一定的问题，并未对此进行校核检验。最后，目前已有的对限流器安装布点的研究普遍是考虑大电网的所有线路，计算量大，存在一定的盲目性。因此，如何简化方案在大电网中安装最少的限流器而又能保证电网可靠安全运行成为解决问题的关键。

综上，本文从短路电流超标对电网动态可靠性影响出发，通过建立可靠性与短路电流、负荷损失之间的量化模型，对电网动态可靠性分析评估，筛选电网薄弱环节，得到基于可靠性的短路问题的简单数学模型。以限流器安装后限流效果及整体均衡度为目标，避免各站点母线对短路电流的限制效果要求不同的问题，进而建立基于可靠性分析的模型和算法，简化网络结构，缩小限流器布点搜索范围。实现可靠性基础上限流器的优化配置，提高电网短路后运行可靠性水平，消除短路后故障扩散隐患。最后以某省实际电网为例，验证了本方案的可行性。

1 特高压接入后短路分析

1.1 特高压接入后网架短路电流水平

特高压在大容量远距离输电方面具有巨大的优势，具有提供输送容量、节约土地资源、降低输电损耗的特点。但特高压接入后的短路电流水平也发生一定的变化。在大电网中，不计及短路支路阻抗的情况下，任一节点的短路电流计算公式为

式中：Zkk为节点阻抗矩阵的对角元素;U·k为故障前节点i上的电压值。

首先，在特高压接入后，区域电网之间的电气距离更加紧密，电气距离缩短，系统阻抗相对减少[10-11];其次，省级电网之间的互联使得整个系统容量更大;最后，特高压建设初期，将同500 kV电网之间形成电磁环网，都会引起特高压接入点的短路电流水平急剧增高。以计划接入特高压的某省电网为例，某省电网计划接入特高压后的网架结构情况如图1所示。

结合图1分析，特高压接入后，电压等级的升高、电气距离的缩短及其组成的电磁环网的紧密程度都会使等值联络阻抗变小，进而导致短路电流急剧增大。表1为特高压接入前后的短路电流增加情况。

由表1可以看出，特高压接入后，其落点附近的母线短路电流均有一定程度的升高，多数母线短路电流增大的幅度高于20%，甚至存在部分母线增幅达到50%以上。因此，要进行特高压工程的建设，需要对规划的网架进行短路电流的计算，并采取相应措施以满足特高压接入后系统能够安全稳定运行的要求。

1.2 限流器短路电流计算

目前提出的限流措施较多，从电网网架结构分析，不同电压等级电网的网架结构不尽相同。可采用简单易行的电磁环网解环方式限制220 kV电压侧过高的短路电流，但也可采用加装限流器的方式。对于500 kV侧电网短路电流的限制，可采用加装限流器的方式，对电网的影响较小，其安装方案主要有以下2种[12]：一种是加装在特高压的500 kV出线上;另一种是为限制特高压系统给500 kV母线提供的短路电流而将其加装在特高压主变500 kV出口处。安装位置具体如图2所示。

结合图1、图2分析，不同电压等级的电网在加装限流器时，其限制效果不同，对于目前限流器的发展情况及经济性问题，220 kV的限流器经济上相对占据优势，但由于该电压等级的线路较多，其分布基本在500 kV站点周边，为有效限制各线路短路电流，则需要安装限流器个数较多，也相对复杂。对于高一级的电压等级500 kV的限流问题，虽然其限流器成本相对较高，但从限流效果分析，安装数量相对较少，又可有效限制周边电压等级低一级的短路电流。

结合文献[6]及短路计算分析，将串联接入1个故障限流器等效为并联问题进行简化，故障下的限流器阻抗值为ZFCL，等效为并联一条支路ZF，但原阻抗矩阵节点数不变。加装限流器等效图如图3所示，利用支路追加法进行分析计算节点导纳矩阵。

加装故障限流器后阻抗矩阵对角元素的变化情况为

自阻抗的变化量为

系统发生短路故障时，支路ij上限流器能够可靠启动的条件是流过该支路的短路电流大于正常电流的3.5倍。此时，加装限流器对超标站点k的限流效果表示为

全网系统的限流水平上限为I0，该值与其相应电压等级断路器的额定遮断电流及相关线路、设备可靠性参数有关，对于部分老线路、变压器等陈旧设备，其限流水平上限I0较低，对于新建变电站、更新变压器等设备、线路的情况，其限流水平上限I0相对较高。此时，为有效限制短路电流到安全范围以内，则安装限流器之后短路电流的变化量必须要高于该母线需要降低的电流最小值，即

由此求出安装限流器阻抗的最小值为

2 电网短路可靠性分析

2.1 电网可靠性分析基础

特高压接入后的系统发生短路故障时，短路电流急剧增大，电网运行状态也随之而发生变化，设备的可靠性降低，故障概率增大。因此短路电流是影响设备可靠性的重要因素之一，设备的动态可靠性水平随短路电流的变化而变化。如何进行有效的动态可靠性评估，建立电网动态可靠性评估与电网故障短路电流下故障率联系，实现短路情况下电网可靠性的准确有效动态评估是本文要研究的基础。

可靠性评估包括静态评估和动态评估，静态评估主要是在运行统计基础上，动态评估与电网运行状态相关。短路情况下的电网可靠性评估是动态可靠性评估的一种，是以设备历史运行统计为基础，考虑短路发生时短路水平，综合得到实际运行中动态可靠性水平。短路情况下动态可靠性主要受系统故障电流、电网运行状态及外界环境等影响。因此，对电网可靠性动态评估主要的依据点也是来自这几类因素的分析研究。因此，有必要对电网运行中动态可靠性的影响因素进行量化分析，本文中主要考虑短路电流因素，建立实际运行相符合的动态可靠性评估模型。

2.2 可靠性综合评估模型

电网发生短路后可靠性分析是一种动态评估过程，尤其是在系统出现短路故障后，电网可靠性随着短路电流变化而变化，在这一动态过程中，短路电流越高，电网可靠性相对越低，呈现负相关。因此，对短路电流水平、故障概率及相应的负荷损失等电气量进行量化拟合，得到可靠性评估的计算公式。结合收集到的各类参数，得到动态可靠性量化结果为

式中：P（Ik）为故障概率与短路电流之间的函数关系，短路电流越高，其故障的概率越高;L（ΔSk）=φ（ΔSk）为故障条件下的负荷损失变化率，ΔSk为负荷容量损失量;C（xk）为常数，即对于特高压接入前的可靠性评估量化值;k表示不同节点数。

负荷容量的计算公式为：

结合实际运行下的统计情况，对故障率与短路电流进行量化拟合，得到与实际运行相似的模拟曲线—S形曲线。S形函数可表示为

式中a、μ为形状参数，具体取值大小与线路、设备有关，线路及变压器等设备的正常工作情况显示出不同的可靠性量化值，因此a、μ取值有所变化，即不同情况下的取值不同。故障率与短路电流之间的关系曲线如图4所示。

图4中：Ik0为短路电流初始值;P（Ik0）为故障概率的初始值。随着系统中短路电流的增大，对设备的稳定运行造成损害也随之上升，电网中发生故障的概率也就越高。当达到一定值时，故障的可能性变成必然的结果。由量化得到的电网动态可靠性评估公式可以看出，在故障率较高且负荷损失率较大的情况下，其评估得到的可靠性量化值越高，对应的可靠性越差，呈现负相关，与前面的分析一致。

3 基于电网可靠性的限流器优化模型

3.1 基于電网可靠性的限流器优化布点

结合对电网动态可靠性量化评估的数学表达式，对所要优化的电网进行可靠性评估，是对电网结构优化的首要任务。综合分析评估结果，找出量化结果中可靠性较低的量，作为限流器安装候选点。在电流越限情况较少且候选点较少的情况下，故障限流器的安装情况较为简单，可直接采用枚举法进行试验。但随着大电网中短路越限站点的增多，故障限流器的安装布点就相对比较复杂，枚举法已不再适用。因此，如何有效缩小优化搜索范围减少计算时间，同时又能够充分考虑电网的可靠性问题，满足电网安全稳定运行成为关键。本文提出基于电网动态可靠性评估的方式在众多限流器可能安装位点中选择出一些候选点，在此基础之上采用优化算法对限流器进行优化配置。具体步骤为：

步骤1）：利用电力系统分析综合程序（power system analysis synthesis program，PSASP）计算全系统所有节点的三相短路电流，找出短路电流超标节点，并记录三相短路电流值。

步骤2）：收集短路电流越限数据、初始可靠性量化参数及故障下的负荷损失率等数据进行量化，并代入电网动态可靠性评估的量化公式进行电网短路的动态可靠性评估。

步骤3）：将量化结果进行整合，找出限流器的安装位置候选点，对此进行下一步优化方案的处理。

步骤4）：取候选支路作为下一步的优化支路，确定限流器安装数量及相应的安装位置，实现全局优化配置。

逐步结合上述步骤进行限流器的安装布点，其目标函数的建立如下文所述。

3.2 限流器优化配置数学模型

从电网规划和运行经济性的角度综合考虑，优化算法的目标是尽可能地减少限流器安装数量而又能有效限制短路电流。在电网动态可靠性评估基础上，选择出限流器布点候选支路，缩小搜索范围。在优化出相应限流方案后，结合实际算例进行验证计算。

限流效果评价函数为

式中：αk为超标点权重，αk=Ik-I0I0=ΔII0，该值的大小与限流器安装前站点短路电流大小有关[13-14]，限流器安装前，短路电流水平越高，其短路电流权重越大;I0为保有一定裕量下的设定短路电流值，由于不同线路的实际可靠性水平不一样，在对短路电流的进行设定时会有所不同，例如新线路中可将参考电流设定为额定遮断电流的90%，而对于部分长线路则只能取70%的额定值作为参考。因此，I0的取值会有所变化。

为避免出现满足限流效果而限流后的各站点母线短路电流差距较大的情况，需要对限流器安装后短路电流限制情况的均衡度进行计算，评价其限流整体效果均衡度情况，优化出最佳的安装方案。因此，建立评价限流后整体水平均衡度的评价函数。

限流整体效果均衡度评价函数为

采用限流器限制短路电流方案需满足3个约束条件：母线短路电流要小于限流目标;限流器阻抗需高于有效限制短路电流时的阻抗最小值;限流器的安装台数满足要求。

1）短路电流约束条件为

2）限流阻抗约束条件为

3）限流器安装台数约束条件为

式中zmax、zmin分别为限流器限流阻抗的最大值、最小值。Nmax为限流器的最大安装个数。

3.3 限流器优化配置算法流程

在考虑限流效果在指定裕量范围内的同时，考虑限流效果的整体限制水平，为简化优化模型，在此，取限流器电抗为10 Ω，个数设置为1～3。其多目标优化函数为：

在限流器的优化配置中，需要对限流水平及整体效果进行综合考虑。结合这两者之间的相关性，构造适应度函数为

式中c1、c2为权重系数，根据实际情况可以对ci值进行选择。

本文采用粒子群算法，该算法具有较强的灵敏性[15-17]，在最优配置问题中应用广泛，在采用该算法进行优化配置后，再结合专业软件对优化方案进行可靠性校核。具体流程如图5所示。

结合图5分析，在对限流器进行优化布点时，由于电网不同环节可靠性不同，短路电流水平的影响不一样，有必要对电网进行可靠性评估，在电网安全可靠运行的基础上有针对性地限制短路电流。首先，应在电网可靠性的基础上对限流器的可能安装位点进行筛选，缩小优化范围;其次，结合电网结构对目标函数中的线路权重以及限流器的安装台数进行设置，并对优化结果进行短路电流计算验证，同时代入到可靠性量化公式中进行校核。如出现不满足短路电流裕量的情况，则调整限流器的个数，重新进行优化计算至满足限流效果及可靠性条件为止。

4 算例分析

4.1 实际电网的可靠性评估

以某省的特高压规划电网为例，在2020年，该省规划接入特高压工程，在规划数据中，由于特高压的接入，其短路电流急剧增大，甚至超出了断路器的额定遮断电流，电网的动态可靠性变差，系统不能正常稳定运行。表2为该省电网在特高压接入前后的短路电流变化。假定所有500 kV电压等级断路器額定遮断电流为63 kA，对规划中电网进行三相短路电流计算。表2为该省特高压接入后某一运行方式下短路电流裕量不足10%的站点。

短路电流对设备及电网安全运行影响较大，电网不同薄弱环节其可靠性不一样。因此，本文采取对电网可靠性分析的方式，有针对性地限制短路电流。通过调研采集数据，结合短路电流计算结果，对该省电网进行动态可靠性评估。图6为在本次部分可靠性评估结果。

结合图6分析，该省电网中相对比较薄弱的站点主要有：MS、NC、YX、LF、JX等，地理位置较为分散。由于后期规划中的站点电气参数缺乏，因此对此不进行可靠性分析，但结合短路电流越限情况进行合理划分其是否作为限流器的候选安装位点，此后对限流器的可能安装位置进行分析。

4.2 实际电网的可靠性评估

基于电网短路的动态可靠性评估，进行限流器的合理安装，有效限制短路电流越限的问题。从经济上考虑，由于限流器成本昂贵，且限流电抗值可变的限流器成本更高，在此，将分析计算中的限流器电抗值固定在10 Ω[18]，仅改变限流器的数量及安装位置。规划中的该省级电网的500 kV站点主要有31个，其候选支路主要有179条，结合故障限流器的动作条件以及通过对电网动态可靠性评估，筛选出可靠性较低的支路安装限流器。系统由原本的179条支路通过筛选减少到38条支路，大大缩小了搜索范围。对支路进行重新编号，设置安装台数为1～3，权重系数各取2/3、1/3。由于实际可靠性参数数据不易收集，因此，为方便计算，本文取短路电流上限统一断路器额定遮断容量的90%。该省规划电网对应不同安装上限数及最佳配置点的适应函数值如表3所示。

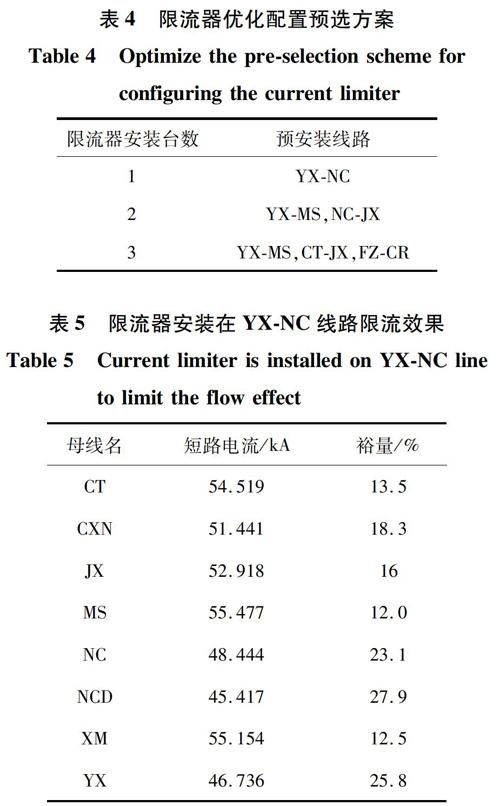
表4为该省电网2020年的限流器优化配置预选方案（重复支路算作一条）。安装台数越多，其经济越高，而由于超高压限流器成本较高，因此设定安装数量不超过3台，故可根据上述限流方案进行方案效果验证。

4.3 限流效果分析

结合4.2节分析及限流器的安装预选方案，对安装限流器后的短路电流进行计算验证，限流器安装台数为1时，安装线路为YX-NC。表5为部分裕量不足站点安装限流器后的短路电流计算结果（断路器的额定遮短容量以63 kA为参考值）。

从表5可以看出，安装一台限流器对安装线路站点短路限流效果明显，同时，其他站点的短路电流裕量均有所上升。该方案满足所有站点短路电流裕量在10%以上，短路电流分布均匀，但整体来看，各站点的短路电流水平均不低，较多站点短路电流裕量在10%～15%之间。结合对电网线路、变压器设备的可靠性量化评估结果分析，部分变电站母线站点的短路电流裕量需要达到20%～30%，例如NC、MS、YX等厂站。因此，从电网动态可靠性分析来看，安装1台限流器并不能有效限制短路电流在安全范围内，电网的安全稳定运行仍受到威胁。

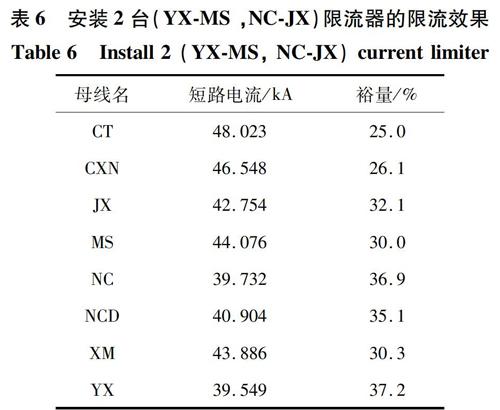
因此，可设置限流器的安装方案为2台，重新进行限流器的优化配置，并对短路电流进行计算。结合表4的安装方案验证分析短路电流水平如表6所示。

结合表6，从总体效果上分析，安装2台限流器时，各站点的短路电流均有很大程度地下降，其短路裕量均有大幅度上升，短路电流裕量均在25%以上，有效限制了短路电流裕量不足的问题。同时，结合电网短路后的动态可靠性评估分析，得到各厂站母线裕量基本满足其线路、设备量化评估后能够安全稳定运行的要求。

为有效试验限流器的最优安装台数，以下对限流器设置个数为3台的效果进行分析。结合表4，对部分裕量不足站点短路电流计算结果如表7所示。

结合表7分析，安装3台限流器的情况下，裕量不足站点短路电流裕量大幅度提升，基本在30%以上，但对于安装线路较远的站点，其短路电流裕量也有所提升，保持在正常范围内。

为验证加装限流器后是否满足电网短路故障下可靠稳定运行的要求，现结合安装限流器后的电网短路电流水平对限流器加装后的电网进行动态可靠性量化评估，其结果如图7所示。

结合图7分析，从限流效果及安装后的动态可靠性分析，安装1台限流器，可以使短路电流裕量保持在10%及以上，但可靠性仍不高。而对于安装2台限流器的情况下，限流效果相对较好，即便是距离限流器安装位置较远，仍满足短路电流裕量值在15%以上。而安装3台限流器，也能有效限制短路电流。基于限流器可靠性运行及价格问题考虑，建议安装2台限流器来限制短路电流，能够在动态可靠性的基础上有效限制短路电流，同时兼顾电网经济性。

5 结 论

本文以特高压接入后短路电流超标问题为背景，从工程实际角度，针对限流器的安装优化配置问题提出了一种基于电网动态可靠性评估的优化方案，并将该方案应用到某省实际电网中进行验证，主要得到以下结论：

1）基于短路情况下的电网动态可靠性评估，充分考虑了电网可能的故障水平及短路越限水平，筛选出可靠性低的位置作为限流器安装候选点，缩小优化布点范围。

2）提出基于可靠性的限流器在大电网中优化配置方法，充分考虑线路、设备可靠性问题，结合不同设备的可靠性情况，进行限流效果的设置。实现在最少的限流器的基础上实现最大限度限制短路电流的效果，同时在经济性前提下，可有效提高电网的运行可靠性水平。

3）对实际电网进行限流器配置，本文在电网动态可靠性的基础上对限流器的布点进行优化。在实际电网的基础上，采用以限制效果及整体均衡度为目标函数，对限流器的安装布点进行优化，在限制电网短路水平的基础上又控制了限制效果的均衡度，有效提升电网整体运行可靠性水平。但可靠性评估仅以故障率及短路电流变化量作为评估标准，对于限流后继电保护的影响并未多做考虑，这是需要进一步研究的问题。

参 考 文 献：

[1] 应林志， 刘天琪， 王建全. 基于改造粒子群游的超高压故障限流器全局优化配置算法[J]. 电力自动化设备， 2018，38（2）：145.

YING Linzhi， LIU Tianqi， WANG Jianquan. Global optimization algorithm for fault current limiter configuration based on rearranged particle swarm optimization[J]. Electric Power Automation Equipment， 2018， 38（2）： 145.

[2] 應林志， 刘天琪， 王建全， 等. 基于改进蚁群优化限制短路电流的网架调整措施[J]. 电力系统自动化， 2018，42（1）：144.

YING Linzhi， LIU Tianqi， WANG Jianquan， et al. Adjustment for power grid configuration to limit short-circuit current based on improved ant colony optimization[J]. Automation of Electric Power Systems， 2018， 42（1）： 144.

[3] 黄根， 罗滇生， 李帅虎， 等. 基于综合灵敏度分析限流的最优断线措施[J]. 电网技术， 2016， 40（1）： 309.

HUANG Gen， LUO Diansheng， LI Shuaihu， et al. Optimal line-outage measure based on comprehensive sensitivity analysis to limit short-circuit current[J]. Power System Technology， 2016， 40（1）： 309.

[4] 陈柏超， 魏亮亮， 雷洋， 等. 饱和铁心型桥式故障限流器的性能参数设计与实验[J]. 电工技术学报， 2017， 32（13）： 185.

CHEN Baichao， WEI Liangliang， LEI Yang， et al. Performance parameter design and experiment of the bridge-type saturated core fault current limiter[J]. Transactions of China Electrotechnical Society， 2017， 32（13）： 185.

[5] 朱霄珣， 徐搏超， 焦宏超， 等. 遗传算法对SVR风速预测模型的多参数优化[J]. 电机与控制学报， 2017， 21（2）： 70.

ZHU Xiaoxun， XU Bochao， JIAO Hongchao， et al. Wind speed prediction mettiod based on SVR and multi-parameter optimization of GA [J]. Electric Machines and Control， 2017，21（2）：70.

[6] 许逵， 孙婷， 韩松， 等. 考虑运行损耗的故障限流器布点优化和容量选择[J]. 电力系统保护与控制， 2015， 43（5）： 21.

XU Kui， SUN Ting， HAN Song， et al. Optimal sittingand parameter selection for fault current limiter constrained with power losses[J]. Power System Protection and Control， 2015， 43（5）： 21.

[7] 胡文旺， 卫志农， 孙国强， 等. 基于灵敏度法的超导故障限流器的优化配置[J]. 电力系统自动化， 2012， 36（22）： 62.

HU Wenwang，WEI Zhinong，SUN Guoqiang，et al.Optimal allocation of superconducting fault current limiters based on sensitivity method[J].Automation of Electric Power Systems，2012，36（22）：62.

[8] 肖怀硕， 李清泉， 张岩， 等. 基于非支配排序遗传改进算法的故障限流器的优化配置[J]. 电网技术， 2016， 40（8）： 2444.

XIAO Huaishuo， LI Qingquan， ZHANG Yan， et al. Optimization offault current limiter configuration based on improved NSGA-2[J]. Power System Technology， 2016. 40（8）： 2444.

[9] 陈柏超， 魏亮亮， 雷洋，等. 基于免疫算法的高温超导故障限流器Pareto多目标优化配置[J].电网技术，2015，39（5）：1343.

CHEN Bochao， WEI Liangliang， LEI Yang， et al. Immune algorithm based pareto multi-objective optimal allocation of high temperature superconductor-fault current limiters[J]. Power System Technology，2015，39（5）：1343.

[10] 茅嘉毅， 蒋平， 胡伟. 采用粒子群算法优化配置限流电抗器的研究及应用[J]. 江苏电机工程， 2010， 29（5）： 21.

MAO Jiayi， JIANG Ping， HU Wei. Research on optimal location of CLI using PSO algorithm and its application[J]. Jiangsu Electrical Engineering， 2010，29（5）： 21.

[11] 李基康，滕欢，郭宁.采用相对熵组合赋权法的500 kV电网短路电流抑制策略优化决策[J].电网技术，2016，40（6）：1811.

LI Jikang， TENG Huan， GUO Ning， Anoptimal decision to restrain short circuit current for 500 kV power grids with combinatorial weighting method of relative entropy[J]. Power System Technology， 2016，40（6）： 1811.

[12] 楼霞薇，王威，王波，等.基于WARD等值的电网限流运行方式优化方法[J].电力系统保护与控制，2017，45（18）：128.

LOU Xiawei， WANG Wei， WANG Bo， et al. A grid operation mode optimization method for controlling short-circuit current level based on WARD equivalence[J]. Power System Protection and Control， 2017， 45（18）：128.

[13] 廖国栋， 谢欣涛， 侯益灵， 等. 特高压接入湖南电网后500 kV母线三相短路电流超标问题分析[J]. 高电压技术， 2015， 41（3）： 747.

LIAO Guodong， XIE Xintao， HOU Yiling， et al. Analysis on theproblems of three-phase short-circuit current over-limited of 500 kV bus when UHV connected to hunan power grid[J]. High Voltage Engineering， 2015， 41（3）：747.

[14] TENG J H， LU C N. Optimum fault current limiter placement with search space reduction technique[J]. Iet Generation Transmission and Distribution， 2010， 4（4）：485.

[15] MEHDINEJAD M，MOHAMMADII B， DADASHZADEHB R， et al. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms[J]. International Journal of Electrical Power and Energy Systems， 2016， 83（142）：104.

[16] 戴水東， 鞠文哲， 夏克文， 等. 采用PSO算法对低压断路器的低能耗优化设计[J]. 电工技术学报， 2017， 32（19）： 100.

DAI Shuidong， JU Wenzhe， XIA Kewen， et al. Optimizationdesign on low energy consumption of low-voltage circuit breakers using PSO algorithm[J]. Transactions of China Electrotechnical Society， 2017， 32（19）： 100.

[17] 武健， 刘子栋， 王超， 等. 基于灵敏度理论的逆变器并网系统谐振特性分析[J]. 电机与控制学报，2018， 22（12）： 11.

WU Jian， LIU Zidong， WANG Chao， et al. Harmonic resonance characteristics of grid-connected system based on sensitivity theory[J]. Electric Machines and Control， 2018， 22（12）： 11.

[18] 应林志， 王建全， 陈迅， 等. 广东电网超高压短路限流器优化配置方案[J]. 电力系统自动化， 2012， 36（4）： 96.

YING Linzhi， WANG Jianquan， CHEN Xun， et al. An optimal configuration scheme for ultra-high voltage short-circuit current limiter in Guangdong power grid [J]. Automation of Electric Power Systems，2012，36（4）：96.

（编辑：邱赫男）

收稿日期： 2018-12-31

基金项目：国家自然科学基金（51467006）

作者简介：章勇高（1975—），男，博士，副教授，研究方向为电力电子在电力系统中的应用、新能源发电系统;

李小蓓（1993—），女，硕士研究生，研究方向为电力系统短路计算;

方华亮（1977—），男，博士，副教授，研究方向为电力系统控制与通信;

龚 俊（1994—），男，硕士研究生，研究方向为电力数据分析。

通信作者：李小蓓