利用DBVC构造虚拟电阻的级联功率变换器稳定控制技术
2020-07-14游江樊志鹏付斌
游江 樊志鹏 付斌
摘 要:针对在级联功率变换器系统中由于高带宽控制的负载侧变换器具有一定的恒功率负阻抗特性,因而可能导致级联系统直流母线电压振荡,并严重影响到整个系统的控制性能和稳定运行的问题,从通过增强级联侧直流母线阻尼来抑制电压振荡的角度出发,提出一种将并联于级联侧直流母线的母线电压补偿装置(DBVC)控制为电阻性的虚拟负载的控制策略及其设计方法。利用级联变换器系统中前后级变换器的输出/输入阻抗,分析和比较了引入所述控制策略前后级联侧直流母线电压稳定性的变化情况。仿真和实验结果表明,所提出的控制方法能够有效抑制级联侧直流母线电压的振荡,可以显著改善整个级联系统的控制性能。
关键词:级联功率变换器;恒功率负载;直流母线电压补偿装置;虚拟电阻;稳定控制
DOI:10.15938/j.emc.2020.06.007
中图分类号:TM 46文献标志码:A 文章编号:1007-449X(2020)06-0055-09
Stabilization control for cascade power converter by utilizing DBVC as a virtual resistor
YOU Jiang1, FAN Zhi-peng1,2, FU Bin3
(1.College of Automation, Harbin Engineering University, Harbin 150001, China; 2. CRRC Dalian R&D Co., Ltd., Dalian 116052, China; 3. School of Light Industry, Harbin University of Commerce, Harbin 150001, China)
Abstract:When voltage oscillation is caused in the cascaded DC bus in a cascaded power converter system, the control performance and stability of the power converter system will be seriously deteriorated accordingly by the inherent constant power load or negative impedance characteristics of load side power converter with high control bandwidth. In order to address this problem, a control strategy is proposed. It suppressed DC bus voltage oscillation through damping enhancement by controlling the parallel DC bus voltage conditioner (DBVC) as a virtual resistor. By using the output impedance of power source converter and the input impedance of load converter, the stability of DC bus voltage was analyzed with and without the proposed control strategy. The simulation and experiment results show that the proposed method can effectively suppress DC bus voltage oscillation and improve control performance for the whole system.
Keywords:cascaded power converter; constant power load; DC bus voltage conditioner; virtual resistor; stabilization control
0 引 言
电力电子功率变换器级联系统是由多个具有完整独立功能的功率变换器通过级联的方法连接起来的,已成为现代先进电力电子系统的基本结构之一。近年来在工业、航空航天、舰船和电动汽车供配电系统以及新能源发电系统等领域都获得了广泛的研究和应用。对于级联变换器系统来说,在控制系统设计上,一般分别以源变换器和负载变换器为被控对象进行独立的设计,虽然这种设计可以保证源变换器和负载变换器独立运行时都能满足设计要求并稳定运行,但是由于源变换器输出阻抗和负载变换器输入阻抗之间的关系可能不满足稳定性判据的要求,而使得所构成的级联系统出现直流母线电压振荡的现象。因此,通过有效地控制措施改善直流母线电压的稳定性对于级联变换器系统的运行是至关重要的[1-2]。文献[3-4]中介绍了使用无源器件改善稳定性的方法,为了避免直接使用电阻导致功率的大量消耗,可使用电阻与电容或电感的串并联组合,包括采用RC串联、RL串联及RL并联的方式。这3种方法均是通过增加系统阻尼来实现系统稳定性改善的目的[5]。虽然这种使用无源器件的方法简便易行,不需要增加任何额外的控制,但电阻的引入终究会导致一定的功率损耗,不可避免地会降低整个系统的效率。
文献[6-7]采用基于纯粹软件算法的有源控制方式来改善级联系统的稳定性。通过将直流母线电压的高频波动分量以前馈的方式注入到负载变换器的控制系统,来改变负载变换器的输入阻抗特性,从而达到改善直流母線电压稳定性的目的。通过引入有源控制的方式,可以在更小直流母线的支撑电容条件下获得母线电压的稳定,可以有效避免使用大容量电解电容可能引起的潜在可靠性问题。并且由于不需要增加额外的无源器件,在系统整体功率密度、损耗和成本方面也具有优势。但是,由于将直流母线电压的波动引入了负载变换器,本质上这是一种以牺牲负载变换器控制性能换取直流母线电压稳定性改善的方法。文献[8-9]通过在前级源变换器的输出与后级负载变换器的输入之间串联充放电状态可控的功率缓冲器来改善级联母线电压的稳定性。额外的串联功率缓冲器的引入不仅改变了原始系统的主电路拓扑结构,并且其成为了整个系统拓扑结构中不可或缺的一部分。除了可能引入额外的可靠性问题,该方式在实际应用时不是非常的方便。
为了考查功率变换器级联系统的稳定性,许多学者针对级联系统的稳定条件进行了研究,建立了多种稳定性判据。Middlebrook阻抗判据[10]是一种常用的稳定性判据,它主要通过判断系统中前级变换器输出阻抗和后级变换器输入阻抗在频域上(通过Bode图)是否存在交叉来确定级联系统是否稳定。其满足稳定的条件苛刻,要求在全频率范围内源变换器输出阻抗Zo均应远小于负载变换器的输入阻抗Zin,即等效环路增益Tm=Zo/Zin<<1。由于Middlebrook阻抗判据相对保守,文献[11]提出了基于禁止区域的阻抗判据。所谓禁区,是指在极坐标平面内设定一个区域,若要使级联系统稳定,则需保证系统的等效环路增益Tm的Nyquist曲线必须在禁止区域之外。目前,基于禁止区域的阻抗判据主要有增益裕度和相位裕度判据(gain margin phase margin criterion,GMPM)、能量源分析联盟判据(energy source analysis consortium criterion,ESAC)及其扩展的根指数稳定判据(root exponential stability criterion, RESC) [12-14]等,这几种判据的主要区别在于其阻抗禁止区域的确定方法有所不同,但不论何种禁区判据,均是基于以下两点考虑提出来的:1)保证级联系统的等效环路增益Tm满足Nyquist判据;2)保证判据具有较强的可操作性。
一般的以时域电流扰动对消为基础的分离结构的母线电压补偿装置(DC bus voltage conditioner,DBVC)方案可以显著增加负载变换器的输入阻抗Zin,而根据Middlebrook稳定性判据,Zin的增加将有助于功率变换器互联(级联)系统稳定性和动态性能的改善[15]。但是这种方法严重依赖于电流检测的准确性,在动态过程中由于可能存在直流母线电流快速突变的情况,若采用一般的基于高通(带通)滤波器来提取直流母线电流交流分量的方法,由于滤波信号中含有直流分量,电流波动在负载变化的初始阶段可能检测不准,从而直接影响到补偿的动态性能。本文采用并联结构的DBVC方案来改善级联系统母线电压的稳定性。利用直流母线电压的波动信息,通过将并联在直流母线上的DBVC控制成为正电阻特性而达到阻尼直流母线电压振荡的目的。本文以下部分首先给出级联功率变换器系统的拓扑和用于系统分析、设计的主要传递函数模型;之后介绍所采用的控制策略的原理,给出将其应用于级联系统的设计方法,并利用EASC判据对系统稳定性改善情况进行分析;最后利用MATLAB/Simulink构建仿真模型,对相关设计和研究结论进行仿真测试,并在搭建的硬件实验平台上进行了验证。
1 拓扑和模型
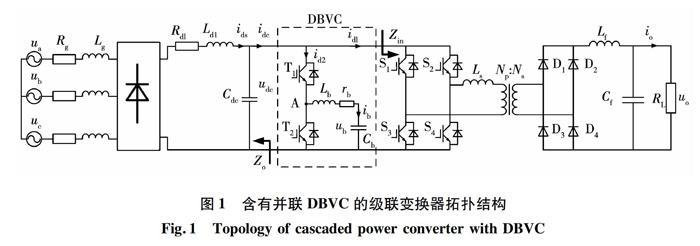
级联功率变换器系统的拓扑结构如图1所示。图中的三相交流电压源、二极管不控整流器以及LC滤波器构成了级联系统的前级源变换器(相当于一个AC/DC电源),移相全桥变换器(phase shift full bridge,PSFB)为级联系统的后级负载变换器。前级的作用是将三相交流电通过二极管不控整流器后转换为直流电,然后再经过LC滤波器平滑滤波后作为移相全桥电路的直流输入。ua、ub和uc是各相交流电压的幅值,Rg为交流进线电感Lg的等效串联电阻,LC滤波器的电感和电容分别为Ld1和Cdc,Rd1为Ld1的等效电阻。图中的AC/DC单元代表了具有较明显输出阻抗的源变换器,考虑上述所有的阻感参数是为了将源变换器的输出阻抗纳入对系统的稳定性分析中。虚线框中所示部分为本文所利用双向半桥Buck/Boost变换器构成的DBVC拓扑结构,T1和T2工作在互补模式,并以T1为主开关管。电容Cb用于暂态能量的缓冲,Lb用于限制高频纹波电流的幅值,rb为Lb的等效串联电阻。
1.1 负载变换器的闭环输入导纳
移相全桥变换器的G参数小信号模型为:
参数小信号模型的控制框图如图2所示。图中:Yi1为开环输入导纳;Gii1为i~o1到i~d1的传递函数;Gid1为d~1到i~d1的传递函数;Au1为u~dc到u~o的传递函数;Zo1为开环输出阻抗;Gud1为d~1到u~o的传递函数;Hv1 为电压控制器;Fm1是等效的脉冲移相调制器传递函数。图中移相全桥变换器相关的传递函数可在文献[16-17]中找到。为使系统获得较高的控制带宽,采用下式所示形式的多极点多零点控制器以使校正后的系统在其自然谐振频率点之后穿越0 dB线,获得较高的控制带宽并使其具有合理的相位裕度,即
式中:ωz1和ωz2為待定的零点角频率;ωp1和ωp2为待定的极点角频率;K为控制器增益。
根据图2的G参数小信号模型框图可得:
联立式(3)中的3个方程,并令i~o1=0(求取输入阻抗时不考虑输出电流的小信号扰动)可以得到移相全桥变换器闭环输入导纳的表达式为
1.2 源变换器的输出阻抗
对图1中级联系统的前级和后级进行等效变换,可得简化等效电路模型如图3所示。
式中Vrms和ωl分别是三相交流电的线电压有效值和角频率。根据图3可得前级源变换器的等效输出阻抗为
利用表1数据可设计移相全桥变换器的控制系统,并研究其直流母线电压的稳定情况。图4所示为负载变换器电压控制系统校正前后的Bode图。可以看出,经过Hv1校正后的系统截止频率约为1.5 kHz,并以-20 dB/dec穿越0 dB线,高频部分以-40 dB/dec衰减,相角裕度约为63°,增益裕度约为31 dB。
根据式(4)和式(6),利用MATLAB仿真软件得到级联系统输出阻抗Zo和输入阻抗Zin的对数频率特性曲线如图5所示。可见,由于输出阻抗的尖峰与输入阻抗交叉的频域低于负载变换器电压环穿越频率(1.5 kHz)以下,此时系统很有可能是不稳定的[19]。图6为根据ESAC禁止区判据(相角裕度和增益裕度分别为60°和6 dB的禁止区域)得出的Yin及其ESAC禁止区域的三维示意图(利用Purdue大学的DC Stability Toolbox获得)。可以看出,Yin及其ESAC禁止区域有明显的交叉,因此也可以判定级联变换器的直流侧母线电压在此情况下是不稳定的。
2 基于虚拟电阻的控制策略
在简化电路图3的基础上引入并联电阻Rvc,如图7所示。图中Zo1表示系统原输出阻抗Zo与虚拟电阻Rvc并联之后的总输出阻抗。
根据图7可列写出以下的微分方程组:
若将具有高闭环控制带宽的移相全桥变换器视为恒功率负载,且其消耗的固定功率为P,则有
式中Ud0代表级联侧母线电压的稳态值。将式(8)带入式(7)中并进行Laplace变换,可以得到系统的特征方程为
通常情况下,Rdc相对很小,在Ud0具有足够数值的情况下完全可以保证式(9)中的常数项大于0,则由Routh判据可得保证系统稳定的条件为
式中Pmax为引入Rvc之前源变换器可以支撑的最大恒功率负载容量。定义R0=-U2d0P表示与恒功率负载对应的负电阻,则根据式(9)可得系统的自然角频率和阻尼系数分别为:
由式(10)和式(12)可见,若引入数值合适的并联电阻Rvc可以抵消R0的作用以增加系统的阻尼比,从而提高原系统抵御恒功率负载的能力。因此,若能通过控制手段使图1所示的并联DBVC支路具有正电阻特性,则可以改善级联侧直流母线电压的稳定性。整个系统的小信号控制框图如图8所示。在图8中右侧所示为基于G参数小信号模型的DBVC控制框图。其中:Yi2为其开环输入导纳;Gii2为i~o2到i~d2的传递函数;Gid2为d~2到i~d2的传递函数;Au2为u~dc到u~b的传递函数;Zo2为开环输出阻抗;Gud2为d~2到u~b的传递函数;Gili为i~o2到i~b的传递函数;Gilu为u~dc到i~b的传递函数;Gild为d~2到i~b的传递函数,上述与DBVC相关的小信号模型及其建立过程可参考文献[20];Fm2为脉宽调制器传递函数。图中通过一个高通滤波器Kf2提取直流母线电压的波动分量u~dh=Kf2u~dc。由于在稳态时图1中DBVC桥臂中点电压uA约为直流母线电压udc的1/2,故根据功率守恒,将u~dh乘以一个比例系数K=2/Rvc之后作为电感Lb的电流指令值,即
这样,通过控制使电感电流ib的波动与直流母线电压udc的波动近似同相位就可实现所述的虚拟电阻控制策略了。此外在图8中,Hi2为DBVC电路中LbCb支路电感电流ib的控制器。如前所述,若以图1中的T1为主开关管,相当于DBVC工作于Buck变换器模式,则图8中的T1占空比扰动d~2到电感电流扰动i~b传递函数可表示为
选择电流控制器的形式为
式中:Kc为增益;ωz和ωp分别为待定的零点和极点角频率。在此,ωp的作用是使校正后的开环系统在直流母线电压谐振频率点(本文约97 Hz)的超前相位有适当地减小。ωz的作用是保证在校正后的开环系统在穿越频率点处具有足够的相位裕度。根据表1所列参数,调整式(15)中ωz和ωp的数值,使校正后的DBVC电流闭环在直流母线电压谐振频率点附近频带处具有近似零相位,以实现虚拟电阻控制策略。
根据图8,利用式(14)和式(15)可得到DBVC电流闭环控制系统的相位角表达式为
在设计过程中,可先根据期望的穿越频率和稳定性要求初步选择合适的ωz、ωp和Kc值。之后可固定一个控制器参数(例如Kc),并根据式(11)将ω固定在直流母线电压谐振角频率ωn上,再分别确定ωz和ωp的变化范围,利用MATLAB绘制θ与ωz和ωp的三维坐标图像来辅助确定更加合适的电流控制器参数值,以使闭环控制的DBVC在直流母线电压谐振角频率ωn附近的相位近似为0,即将DBVC控制为电阻特性。DBVC电流闭环控制系统的三维相位图如图9所示,采用式(15)所示形式的控制器,在ωz和ωp较大范围变化情况下可获得θ在ωn附近近似零相位的特性,即可将DBVC控制为近似电阻特性。
选择合适的电流控制器参数,校正后的电流环穿越频率约为1.65 kHz,幅值裕度约16 dB,相位裕度约61°,如图10所示。
又根据图8可得到如下方程组:
根据式(18)可得到控制为虚拟电阻的DBVC输入导纳表达式为
利用表1所列的参数,根据式(10)可得源变换器所能支撑的最大恒功率负载Pmax≈280 W。突加负载(RL由8 Ω突變为1.7 Ω)前的负载功率P1=200 W
3 仿真与实验验证
为了验证所提出控制策略的有效性,本文在MATLAB/Simulink环境中搭建了系统仿真模型进行仿真测试,仿真参数如表1所示。
图13为不施加所述DBVC控制策略的仿真波形。0.3 s之前系统带载200 W,级联系统工作在稳定状态,0.3 s时突加负载至940 W,由于后级的移相全桥变换器具有较高的控制带宽而呈现一定的恒功率负阻抗特性,因而级联侧的直流母线电压和移相全桥变换器的输出电压出现了剧烈的振荡。
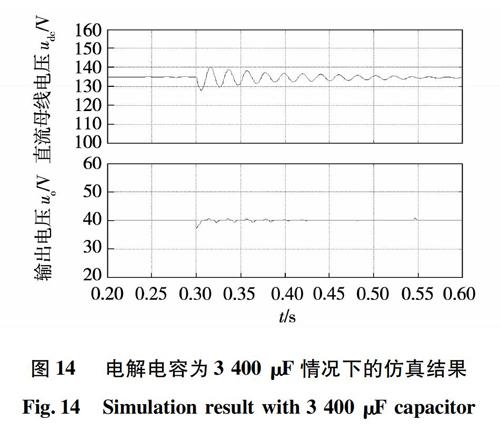
图14是将直流母线电容从900 μF增大到3 400 μF的仿真波形,通过观察波形可以看出,当负载变换器0.3 s加载后,由于增大了最大恒功率负载容量Pmax,直流母线电压和移相全桥变换器的输出电压振荡现象得到了改善,经过约0.25 s的调节后,直流母线电压和输出电压趋于稳定。
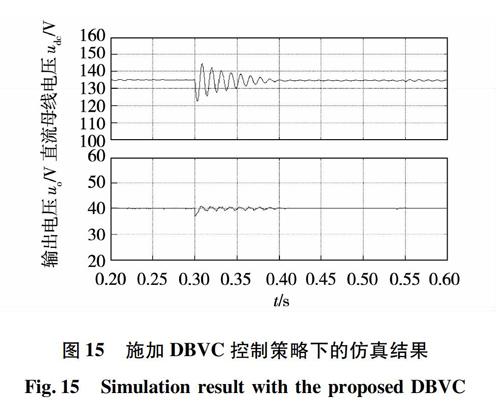
图15为将DBVC控制成虚拟电阻情况下的仿真波形,同样在0.3 s时对移相全桥变换器突加负载功率至940 W,直流母線电压和移相全桥变换器的输出电压在经过0.1 s的调整后逐渐趋于稳定。
在仿真测试及分析的基础上,构建硬件系统对上述设计和仿真结果进行进一步的实验验证,实验的负载变化情况与仿真测试一致,实验结果如图16~图18所示。图16为后级移相全桥变换器突加至940 W负载的实验波形,可见加载后,不仅级联侧的直流母线电压出现剧烈地振荡,而且移相全桥变换器的输出电压也出现明显地波动,整个系统处于失稳状态。这与上文频域分析和时域仿真的结果是吻合的。
作为对比,将前级整流输出的直流母线电解电容增大到3 400 μF,考查其对直流母线电压稳定性的影响,实验波形如图17所示。可见在此情况下突加相同的负载后,直流母线电压在衰减振荡后可恢复稳定状态。后级移相全桥变换器的输出电压在母线电压衰减振荡过程中出现比较轻微波动,但可以很快恢复到平稳输出状态。
图18是采用本文所述方法将DBVC控制为虚拟电阻的实验波形。在实验中级联侧直流母线电容保持为900 μF,DBVC中的电容Cb容量约为560 μF。从实验波形可见,负载突加到940 W后,级联侧直流母线电压可在约0.1 s时间内恢复稳定。在此情况下,虽然母线电压在衰减振荡的初始阶段振荡幅值高于图17中采用3 400 μF电解电容的情况,但在采用DBVC的情况下总的电容量为1 460 μF,这在一定程度上有助于减小系统的体积和重量。
4 结 论
本文以一种前级为不可控AC/DC变换器、后级为移相全桥变换器的级联变换器为例,利用小信号模型并以Bode图和ESAC判据为工具,研究和分析了级联功率变换器的母线电压稳定性问题。针对导致级联侧直流母线电压振荡的原因,提出一种将DBVC控制为等效正电阻以改善直流母线电压稳定性的控制策略,并通过仿真和实验结果验证了所提控制策略的正确性和有效性。
参 考 文 献:
[1] 杜韦静, 张军明, 钱照明. Buck变流器级联系统直流母线电压补偿控制策略[J]. 电工技术学报, 2015, 30(1):135.
DU Weijing, ZHANG Junming, QIAN Zhaoming. Compensation methodology for DC bus voltage of cascaded system formed by Buck converters[J]. Transaction of China Electrotechnical Society, 2015, 30(1):135.
[2] 钟志宏, 方晓春, 林飞, 等.MTPA控制下逆变器-IPMSM系统直流侧电压稳定性研究[J] . 电工技术学报, 2017, 32(21):34.
ZHONG Zhihong,FANG Xiaochun,LIN Fei,et al.DC voltage stability studies with IPMSM system under the control of MTPA[J].Transaction of China Electrotechnical Society,2017,32(21):34.
[3] CSPEDES M, BEECHNER T, XING L, et al. Stabilization of constant-power loads by passive impedance damping[C]// Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), February 21-25, 2010, Palm Springs, CA. 2010: 2174.
[4] JUSOH A B. The instability effect of constant power loads[C]// Proceedings National Power and Energy Conference, November 29-30, 2004, Kuala Lumpur, Malaysis. 2004: 175.
[5] CESPEDES M, XING L, SUN J. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7):1832.
[6] LEE W J, SUL S K. DC-link voltage stabilization for reduced DC-link capacitor inverter[J]. IEEE Transactions on Industry Applications, 2014, 50(1): 404.
[7] MAGNE P, MARX D, NAHID-MOBARAKEH B, et al. Large-signal stabilization of a DC-link supplying a constant power load using a virtual capacitor: impact on the domain of attraction[J]. IEEE Transactions on Industry Applications, 2012, 48(3):878.
[8] LOGUE D, KREIN P T. The power buffer concept for utility load decoupling[C]// IEEE 31st Annual Power Electronics Specialists Conference, June 23, 2000, Galway, Ireland. 2000:973.
[9] LOGUE D L, KREIN P T. Preventing instability in DC distribution systems by using power buffering[C]// IEEE 32nd Annual Power Electronics Specialists Conference, June 17-21, 2001, Vancouver, Canada. 2001: 33.
[10] MIDDLEBROOK R D. Input filter considerations in design and application of switching regulators[C]// Proceedings of the IEEE Industry Applications Conference, May 15-19, 1979, Cleveland, USA. 1979: 366.
[11] WILDRICK C M, LEE F C, CHO B H, et al. A method of defining the load impedance specification for a stable distributed power system[J]. IEEE Transactions on Power Electronics, 1995, 10(3): 280.
[12] SUDHOFF S D,GLOVER S F,LAMM P T,et al. Admittance space stability analysis of power electronic systems[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(3):965.
[13] SUDHOFF S D, CRIDER J M. Advancements in generalized immittance based stability analysis of DC power electronics based distribution systems[C]// IEEE Electric Ship Technologies Symposium, April 10-13, 2011, Alexandria, USA. 2011:207.
[14] FENG X, YE Z, XING K, et al. Individual load impedance specification for a stable DC distributed power system[C]//Fourteenth Annual Applied Power Electronics Conference and Exposition, March 14-18, 1999, Dallas, USA. 1999: 923.
[15] XING K, GUO J, HUANG W, et al. An active bus conditioner for a distributed power system[C]// 30th Annual IEEE Power Electronics Specialists Conference, July 1,1999,Charleston, USA. 1999: 895.
[16] VLATKOVIC V, SABATE J A, RIDLEY R B, et al. Small-signal analysis of the phase-shifted PWM converter[J]. IEEE Transactions on Power Electronics, 1992, 7(1): 128.
[17] 吳涛, 阮新波. 分布式供电系统中源变换器输出阻抗的研究[J]. 中国电机工程学报, 2008, 28(3):66.
WU Tao, RUAN Xinbo. Output impedance analysis of source converters in the DC distributed power system[J].Proceedings of the Chinese Society for Electrical Engineering,2008,28(3):66.
[18] HARNEFORS L, PIETLINENARDIER K. Inverter DC-link stabilizing control with improved voltage sag ride-through capability[C]//IEEE European Conference on Power Electronics and Applications,September 11-14,2005,Dresden,Germany. 2005:1.
[19] 张欣, 阮新波. 用于提高级联型电源系统稳定性的自适应有源电容变换器[J]. 电工技术学报,2012, 27(2):23.
ZHANG Xin,RUAN Xinbo.Adaptive active capacitor converter for improving the stability of cascaded DC power supply system[J].Transaction of China Electrotechnical Society,2012,27(2):23.
[20] SUNTIO T. Dynamic Profile of Switched-Mode Converter: Modeling, Analysis and Control[M]. Hoboken, New Jersey, USA:Wiley,2009:64-77.
(编辑:邱赫男)
收稿日期: 2018-03-02
基金项目:国家自然科学基金(51479042);国家自然科学基金重点项目(51761135013);黑龙江省自然科学基金(F2016007);中央高校基本科研业务费(HEUCFG201822)
作者简介:游 江(1977—),男,教授,博士生导师,研究方向为电力电子技术及应用;
樊志鹏(1992—),男,硕士,助理工程师,研究方向为电力电子技术及应用;
付 斌(1972—),男,副教授,硕士生导师,研究方向为控制理论及应用。
通信作者:付 斌
