基于粒子群算法的智能车辆多目标跟踪

孙柱 赵强 张娜 朱宝全 王娜

摘 要：针对智能车辆在公路行驶过程中对其他运动车辆的实时跟踪问题，提出基于离散二进制粒子群算法的多目标物体跟踪方法。本文通过基于雷达数据建立跟踪目标的状态方程和测量方程，将雷达多个扫描周期的测量数据进行关联，形成含有可能轨道的多种假设，利用似然率对轨道进行评分，形成混合整数线性规划问题，并采用离散二进制粒子群算法进行求解。解决各个时刻测量值和目标的关联问题，实现对跟踪目标的轨道判别。最后通过在MATLAB中进行仿真，验证了算法的有效性。

关键词：智能车辆;多目标跟踪;多假设跟踪;卡尔曼滤波;粒子群算法

Abstract：Aiming at the problem of simultaneous tracking of other vehicles in the process of intelligent vehicles driving on the road， a multi-object tracking method based on binary particle swarm optimization is proposed. In this paper， the state equation and measurement equation of tracking target are established based on radar data， the measurement data of multiple scanning periods of radar are correlated to form a variety of assumptions with possible orbit， and the orbit is scored by likelihood ratio to form a mixed integer linear programming problem， which is solved by discrete binary particle swarm optimization algorithm. The problem of correlation between the measured value and the target at each time is solved， and the track discrimination of the tracking target is realized. Finally， through the simulation in MATLAB， the data results verify the effectiveness of the algorithm.

Keywords：Intelligent vehicle; multi-objective tracking; multi-hypothesis tracking; Kalman filtering; particle swarm optimization

0 引言

智能汽車在自动驾驶时必须要具有的环境感知功能是智能车辆跟驰、超车及二次路径规划的前提。通过雷达在一定时间间隔内扫描的数据判别出每个移动车辆属于多目标跟踪问题。多假设跟踪是多目标跟踪领域中解决目标与数据关联问题比较有效的算法。尹文进等[1]将MHT算法用于水下航行器对多个探测目标点的航迹实现了有效分离。杨飞等[2]利用多假设跟踪对三维激光雷达数据进行关联，并解决了漏检及虚警的问题。邵洁[3]采用卡尔曼滤波算法实现跟踪轨迹假设，并用LAP算法来实现数据关联。屠亚兰[4]提出的改进结构化分支多假设跟踪算法，在航迹置信度函数中引入了目标径向速度信息。

Symbol`@@

孙进平等[5]提出一种基于超图匹配的多假设群目标跟踪方法，通过延迟决策、超图匹配等来实现群分离和融合判断以及群内个体的目标数据关联。费自刚等[6]结合似然函数和多假设跟踪算法，在主动声呐检测中实现了主动目标断续跟踪问题。武文斌等[7]使用Lucas Kanada跟踪方法来对图像中标定的特征点进行跟踪，并对所跟踪误差通过子图像匹配法进行矫正消除。本文以公路上运行的智能车辆自动驾驶工况为应用场景，研究采用多假设跟踪算法进行移动多目标车辆的跟踪。考虑到多假设跟踪算法对假设路径的剪裁归结为一个离散约束优化问题，本文采用离散二进制粒子群算法进行求解，最后通过MATLAB进行数值仿真来验证本文算法的有效性。

1 目标跟踪问题描述

在智能车辆行驶过程中，取车辆的位置x、y，车辆的速度vx、vy，车辆的横摆角θ和横摆角速度ω为系统状态，写成状态向量形式为：X=[x，y，vx，vy，θ，ω]T，被其跟踪的车辆运动方程为[8]：

2 基于多假设的多车辆跟踪

3 数值仿真

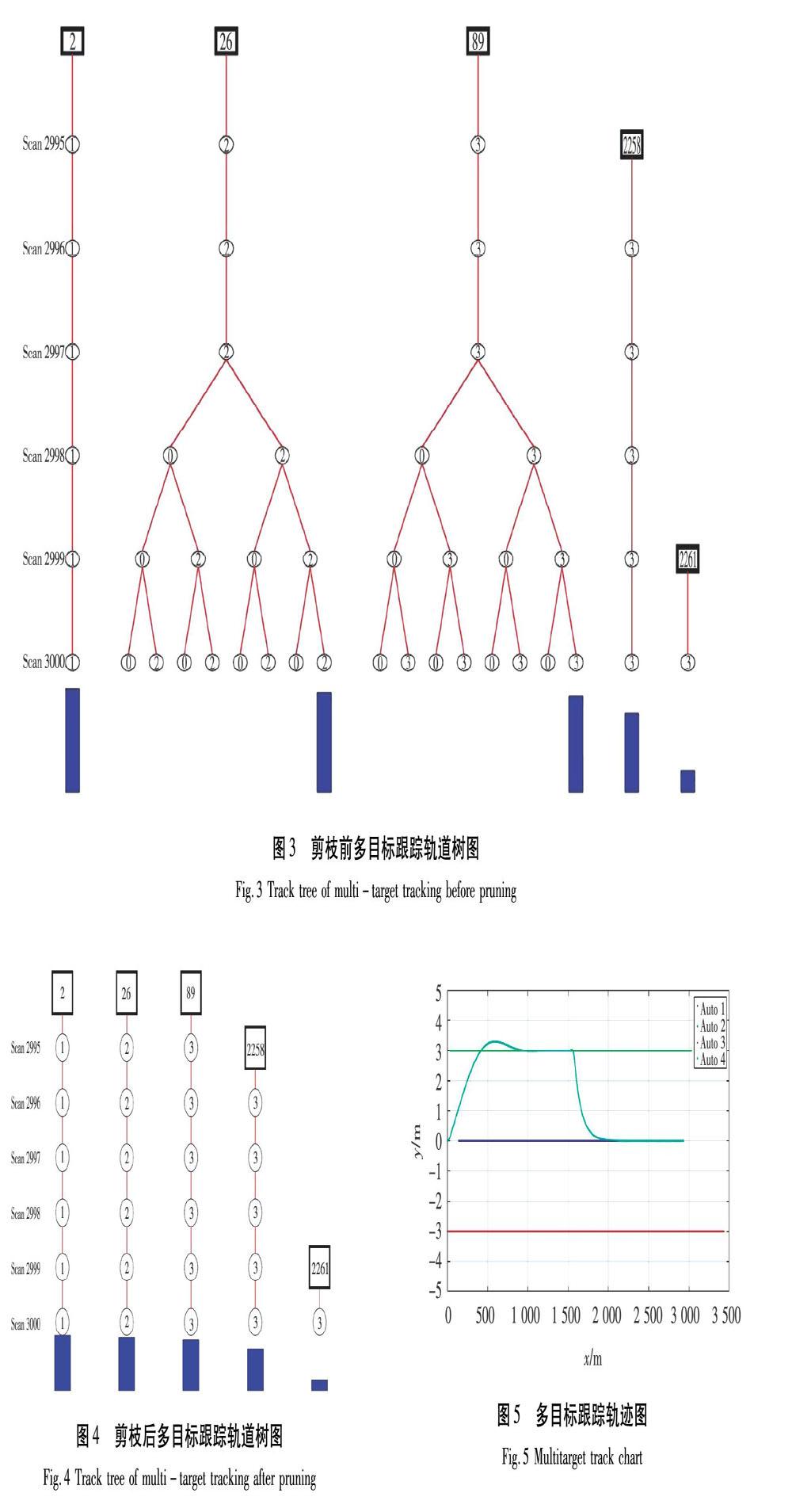
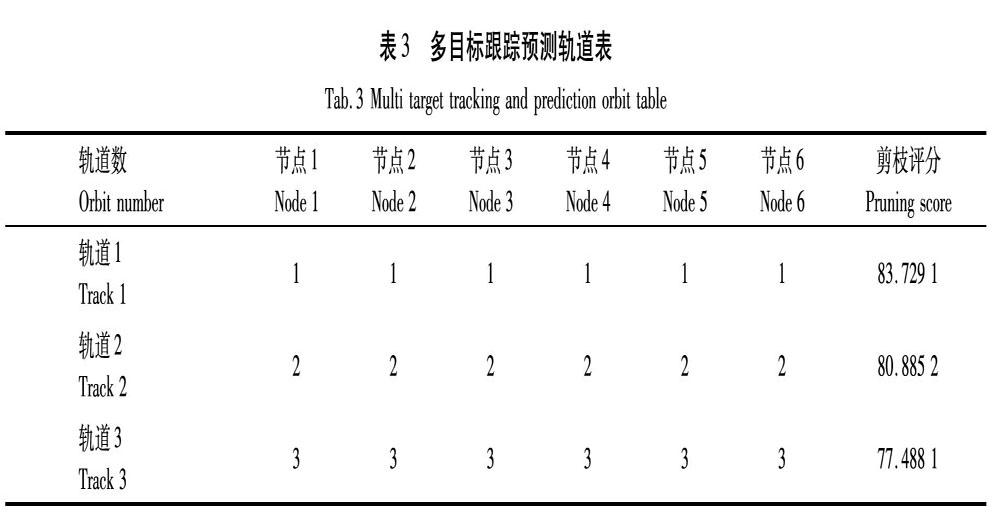
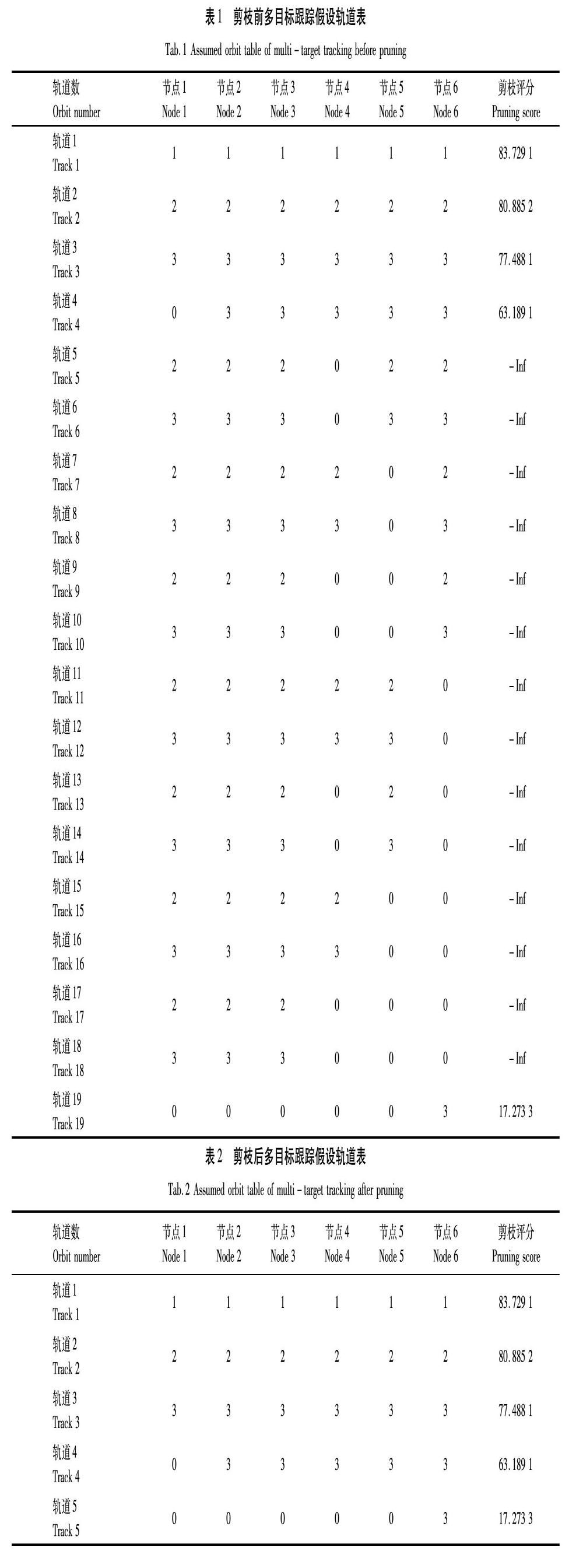
本文模拟公路行驶的智能车辆在单向道路中，通过车载雷达进行6次扫描，前2次与后4次共探测到7个移动目标，设定智能车扫描到的周围移动障碍物即视为移动车辆。利用本文算法将测量值分配到对应轨道，通过剪枝、评分，使系统能够自主和可靠地追踪4辆汽车。采用MATLAB编写m文件并运行，所有跟踪假设轨道见表1。通过进行轨道剪枝、评分得出5条待选轨道，见表2。并选取评分最高的前3条轨道，表3中为在仿真结束时预测显示的3条轨道，与实验对比正是所期望的结果。

将MATLAB运行仿真的多目标跟踪轨道树图显示全部假设的轨道树结果，并对各轨道树进行评分，以柱状图的形式表现出来。如图3所示。对轨道树进行剪枝、评分后其具体形式如图4所示。图5则是经过轨迹剪枝、滤波、预测，并最终输出的多目标跟踪轨迹图，其中车辆1为智能车，车辆2—车辆4为前后两时刻跟踪的3辆目标车辆。

4 结论

本文针对智能车辆在公路运行工况下提出基于二进制粒子群算法的多目标物体跟踪，通过卡尔曼滤波算法对多目标运动状态进行准确的预测估计，采用的多假设跟踪算法对雷达数据进行关联，从而得到轨道树评分，其前3名轨道号分别为2号、26号、89号，且对应的剪枝评分分别为：83.729 1、80.885 2、77.488 1，其分值满足最低评分要求。则上述关联的3个轨道即为跟踪车辆的预测轨道。由此解决了各个时刻的测量值和目标的关联问题，实现了对多个车辆的有效跟踪。

【参 考 文 献】

[1] 尹文进， 张静远， 饶喆. MHT算法在航迹关联中的应用[J]. 兵工自动化， 2016， 35（4）： 40-41.

YIN W J， ZHANG J Y， RAO Z. Application of multi hypothesis track algorithm in track association[J]. Ordnance Industry Automation， 2016， 35（4）： 40-41.

[2]楊飞， 朱株， 龚小谨， 等. 基于三维激光雷达的动态障碍实时检测与跟踪[J]. 浙江大学学报（工学版）， 2012， 46（9）： 1565-1571.

YANG F， ZHU Z， GONG X J， et al. Real-time dynamic obstacle detection and tracking using 3D Lidar[J]. Journal of Zhejiang University （Engineering Science）， 2012， 46（9）： 1565-1571.

[3]邵洁. 基于MHT的多物体跟踪算法[J]. 上海电力学院学报， 2010， 26（1）： 79-82.

SHAO J. Multiple target tracking based on MHT[J]. Journal of Shanghai University of Electric Power， 2010， 26（1）： 79-82.

[4]屠亚兰. 一种改进的结构化分支多假设跟踪算法[J]. 现代雷达， 2011， 33（12）： 28-32.

TU Y L. A modified structured branching multiple hypothesis tracking algorithm[J]. Modern Radar， 2011， 33（12）： 28-32.

[5]孙进平， 付福其， 付锦斌， 等. 应用超图匹配的多假设群目标跟踪方法[J]. 信号处理， 2017， 33（11）： 1497-1504.

SUN J P， FU F Q， FU J B， et al. Multiple hypothesis group target tracking using hypergraph matching[J]. Journal of Signal Processing， 2017， 33（11）： 1497-1504.

[6]费自刚， 任凯威. 主动声呐多假设跟踪算法的一种改进[J]. 声学与电子工程， 2018，33（3）： 9-12.

FEI Z G， REN K W. An improvement of active sonar multi hypothesis tracking algorithm[J]. Acoustics and Electronics Engineering， 2018， 33（3）： 9-12.

[7]武文斌， 毋立芳， 王晓芳， 等. 一种点相关统计特性的目标跟踪方法[J]. 中国科技论文， 2012， 7（1）： 28-32.

WU W B， WU L F， WANG X F， et al. Robust object tracking approach using point correspondences[J]. China Sciencepaper， 2012， 7（1）： 28-32.

[8]迈克尔·帕拉斯泽克， 斯蒂芬妮·托马斯著. MATLAB与机器学习[M]. 李三平， 陈建平，译.北京： 机械工业出版社， 2018.

PALUSZEK M， THOMAS S. MATLAB machine learning[M]. Translated by LI S P， CHEN J P. Beijing： China Machine Press， 2018.

[9]黄小平 王岩. 卡尔曼滤波原理及应用[M]. 北京：电子工业出版社，2015.

HUANG X P， WANG Y. Kalman filter principle and application[M]. Beijing： Electronic Industry Press， 2015.

[10]郭文忠 陈国龙. 离散粒子群优化算法及其应用[M]. 北京：清华大学出版社，2012.

GUO W Z， CHEN G L. Discrete particle swarm optimization algorithm and its application[M]. Beijing： Tsinghua University Press， 2012.