“板块”模型的能量问题探析

张玲

【摘 要】本文论述“板块”模型中的能量问题，从实例出发，细化分析解题思路，有效找到解决问题的突破口，帮助学生更好地掌握解决问题的方法。

【关键词】“板块”模型 摩擦力 能量

物理是一门严谨的逻辑学科。物理问题其实就是关注物体的运动问题→关注物体为什么能发生该运动的问题→关注物体运动过程中的能量转化问题等。分析物体运动过程中能量转化问题是高考中常见考点，“板块”模型又是该问题中的典例。与此同时，这也是相当一部分同学惧怕的考点。故本文以此点切入，整理、讨论处理该问题中的常用有效方法。

一、构建模型：板块模型

简要整理板块模型，最基本为“一板 + 一块”，其中滑块的一般特征为大小可以忽略，拓展模型有子弹打木块等。如图 1 所示。

二、问题分析

物理问题的处理忌讳在分析不透彻的情况下，胡乱套用公式。虽然有时候答案碰巧对，但分析过程是无效的，并没能抓好处理问题的本质。做好运动分析在前，能量分析才能顺利随后。在“板块”问题中怎么样才能够清晰准确地做好运动分析呢？归一思路，物理问题中对运动分析的逻辑是一致的。分步走：（1）确认研究对象;（2）明确初始条件;（3）正确进行受力分析。将几个步骤结合在一起，才能对运动过程做准确的判断。在“板块”运动分析中，摩擦力是关键。摩擦力分为两种，一为静摩擦力，二为滑动摩擦力。简要回顾二者的做功特点：

1.静摩擦力做功的特点

（1）静摩擦力有的情况下做正功，有的情况下做负功，甚至还有的情况下可以不做功。

（2）相对静止有运动趋势的物体之间才会存在静摩擦力，故对两个相互作用的物体做功代数相加肯定等于零。

（3）静摩擦力做功时，能量肯定不会发生转化，仅会在相互作用的两个对象之间转移。

2.滑动摩擦力做功的特点

滑动摩擦力有的情况下做正功，有的情况下做负功，有的情况下不做功。

举例，长木板停在光滑的地面上，板与块间的滑动摩擦力大小为 f，其中板质量为 M板，块质量为 M块。

经过分析，其中的滑动摩擦力分别对板、块做功，涉及的能量为动能和内能。根据能量转化的情况，可以作出进一步归纳。

三、方法归纳

1.能量守恒定律是自然界中不需要任何条件就恒成立的规律，因此相互作用“板块”间的能量问题由此切入。经过分析系统初态的机械能及末态机械能发现有差量，这个差量能量不会消失，只是转化成热量，其关系如下：

2.功和能一直无法分割。力做了多少功，定会有相应能量发生转移或者转化。从该角度分析并结合式子整合运算后发现，滑动摩擦力对系统做的功刚好等于系统内能的增加量，即 Q= fx相，其中 x相 为相互作用的两个对象的相对位移。特别需要提醒的是，有相对往返运动时，问题较繁琐，本文暂不举例。

对比并整理大量例子后发现，“板块”模型中最典型的能量转化问题为其他形式的能量转化为内能的问题。从能量守恒切入，上述两个基本方法适用面非常宽。

四、方法例析

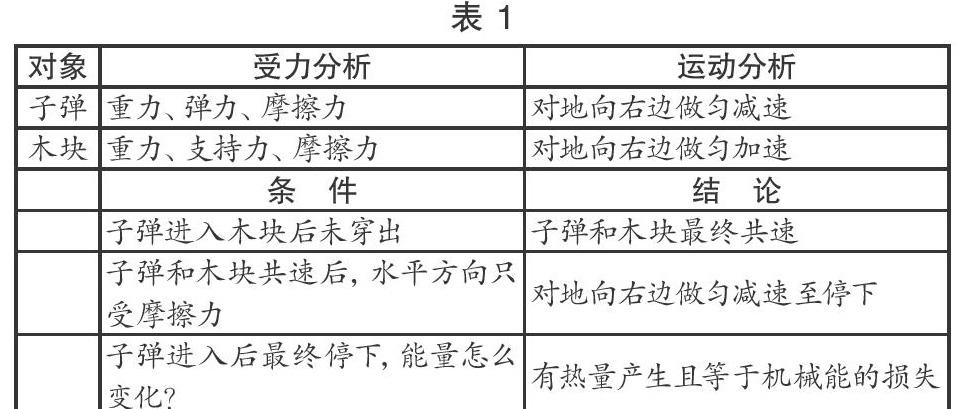
【例 1】如图 3 所示（见下页），粗糙地面上放置了一个木块，其质量为 M块。一子弹的质量为 m，在极短时间内以速度 v 沿水平方向射入木块，且未穿出。若木块与地面间的动摩擦因数为 μ，重力加速度为 g。求：

（1）木块最终在地面上前进的距离 s;

（2）求二者相互作用過程中系统增加的内能 Q。

本题在考虑能量转化过程中，采用了能量守恒的思路进行处理。

【例 2】滑块 B 被轻放在木板水平的上表面，滑块质量为 M块，木板初态为静止，其质量为 M板。已知木板长为 L，二者动摩擦因数为 μ，重力加速度为 g。现用水平向右的恒力 F 拉滑块 B，A、B 会发生相对运动。

（1）当 B 从 A 的右端滑出时，长木板 A 的位移是多少？

（2）请求相互作用过程中产生的热量。

本题在处理能量转化过程中，主体应用能量守恒的思路。拉力 F 对滑块做的正功等于 A、B 动能的增加量和 A、B 间产生的热量总和，最终导出的结果 Q=μM块gL，其中 L 为二者的相对位移。可见，前面运动分析铺垫到位，复杂情境也会变得清晰。以此类推，再解决一个类型题。

【变式】光滑的水平面上停着一辆长度为 L，质量为 M 的平板小车。在小车的最左端轻放一个质量为 m 的物块，物块受到水平恒力 F 作用且恰能滑到小车的右端。其中小物块与小车之间的摩擦力为 f，经过一段时间小车运动的位移为 x，则下列说法中正确的是（ ）。

A.此时物块的动能为 F（x+L）

B.此时小车的动能为 fx

C.该过程中，系统机械能增量为 Fx-fL

D.这一过程中，因摩擦而产生的热量为 fL

本题考查的能量转化比较复杂，但同样可以运用类似的逻辑思路分析。分析思路如下：

综合受力分析和运动简图，明确物体和小车的位移。A 选项需要解决对象的末态动能问题，优先考虑用动能定理。其中对物块有：（F-f）·（x+L）=EK-0，故 A 错误;对小车有：fx=E′k-0，B 正确;系统增加的机械能可以将二者的末态动能相加，则 C 错误;摩擦生热部分可以尝试用本文主要阐述的两个观点处理：（1）能量守恒的观点 F（L+x）=EK+E′k=fL;（2）功和能量的转换对应关系 Q=fL，D 选项正确。

五、结语

部分同学惧怕“板块”间能量问题的分析，很大程度是因为这个问题会出现在多物体的运动过程中。因为无法准确分析物体的运动情况，所以对能量问题无法判断。

本文所举的运动例子较为简单，意在凸显解决“板块”模型中能量问题的基本步骤。对比下来，各题均有相通的逻辑分析，有可以跟进的基础分析步骤，有共同的突破口等。如果遇到多物体多过程的问题又该如何处理？其实，复杂的问题都是由多个子过程组成。分析这些过程时，需要将全程分割成多个子过程，再分别对子过程进行处理，本文暂不对综合问题展开讨论。

关于“板块”模型的能量问题的设计可以多样化，但笔者希望能够理清分析问题的基本逻辑，掌握物理思维的核心点。毕竟，解决物理的问题，并不是单纯地为了解决物理题。

【作者简介】张 玲（1986— ），物理学本科，一级教师，现就职于南宁市第二中学，任高三物理备课组长，曾获全国物理教师技能大赛一等奖，南宁市优质课比赛决赛第一名，研究方向：高中物理教学。

（责编 卢建龙）