GPS水准高程转换模型在工程测量中的应用研究
2020-07-14李志懂
李志懂
(广东裕有勘测科技有限公司,广东 肇庆 526000)
0 引言
GPS测量技术具有实时、快速、全天候等特点,已在测绘行业得到广泛的应用,GPS在平面测量时能够达到较高的精度,受制于大地水准面的误差以及不同地区高程异常值的不同,GPS技术在高程测量方面始终差强人意。相关学者提出了构建相应的数学模型,采用GPS高程拟合的方法将GPS测量的大地高转换为正常高,从而来替代常规繁琐的水准测量,常用的GPS高程转换模型主要有线性拟合、曲面拟合等方法,具体过程就是在工程测量中结合实际的地形,选用合理的GPS高程转换模型,但在不同的地形测量区域,不同的GPS高程转换模型结果会有较大的差异,由此,本文结合实例,对GPS水准高程转换模型在工程测量中的应用进行了相关探讨。
1 工程概况
某测区位于某市工业园区内,总面积13.17 km2,测区地势平坦,前期已布置三、四等GPS平面控制网,总计有28个控制点,其中三等控制点11个、四等控制点17个。三等GPS平面控制网利用GPS接收信号机开展GPS高程测量,采用1985国家高程基准;四等平面控制网同步观测,结合部分三等控制点,获得项目区域测量点数据,同时将其作为工程校核数据。采用专业平差计算软件对水准网进行平差计算,分别计算出水准网内各个控制点的平差值,保证各个数据点精度符合规范要求,可采用这一系列数据点作为高程拟合模型的基础点。
2 GPS水准高程拟合模型的应用分析
根据28个控制点的数据,计算出各个控制点的高程异常值,并绘出高程异常值趋势图(见图1)。从图2可以看出,测量区域28个控制点的高程异常值范围为11.33~11.79 m。
获得28个控制点数据后,选定平面拟合、二次曲面、三次曲面、距离加权、移动二次曲面、抗差二次曲面、移动抗差二次曲面及多面函数模型共8个模型进行GPS水准高程拟合,并利用Matlab编程技术计算出各个模型的精度参数值,综合评估确定适合项目区域的拟合模型。
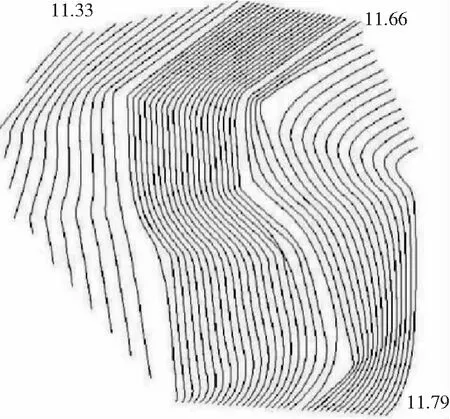
图1 高程异常值
2.1 内符合精度
内符合精度包含拟合模型计算的中误差、最大残差、最小残差。8个模型的内符合精度中,多面函数模型的中误差最大,为0.183 m;二次曲面的中误差最小,仅有0.013 3 m。多面函数模型的最大残差值最大,为0.36 m;二次曲面的最大残差值最小,仅有0.031 7 m。距离加权模型的最小残差值最大,为0.006 m;二次曲面的最小残差值最小,仅有0.000 3 m。综合中误差、最大残差及最小残差来看,二次曲面模型精度较高,适用于工程区域GPS水准高程转换。
2.2 残差分布统计
各个模型残差分布差异较大,根据不同模型下所有测量控制点的残差值分布统计,了解8个转换模型的残差分布情况,确定转换模型精度较高者。
从残差值分布来看,残差大于5 cm的控制点最多的是多面函数模型,达19个,其中残差超过4 cm的控制点有20个,占比超过71.4%。残差在2 cm以内的控制点最多的是移动二次曲面,达26个;二次曲面模型中残差在2 cm以内的控制点有24个,占比超过85.7%。在GPS水准高程拟合过程中,高程异常值在一定程度上有未知性,因而采用多面函数模型进行拟合转换。当控制点分布不均匀时,可能会出现“插值振荡”,造成多面函数模型残差值分布出现急剧增大或减小的情况。
根据残差分布统计,绘出各个模型的残差分布直方图(如图2所示)。从图中可看出,在残差低于1 cm的控制点中,除距离加权与多面函数模型外,其他6个模型拟合精度相符。其中二次曲面模型残差分布更为稳定,残差在3 cm 以内的控制点占比超过90%。经内业复核证明,中误差绝对值仅有1.36 cm,满足《城市测量规范》起算点要求。因而,在这个8个转换模型中,采用二次曲面模型进行GPS水准高程转换较为合适。
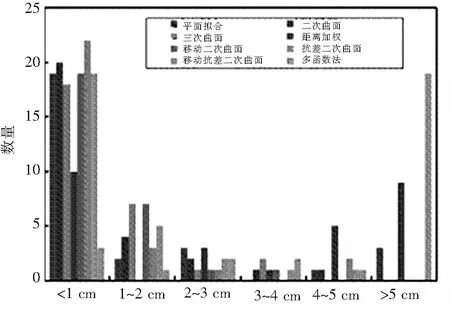
图2 残差分布直方图
2.3 外业精度检测
为确保选用的GPS水准高程模型的合理性,采用外业检测手段进行校核,获得外业精度特征值,分析GPS水准高程模型的适用性。为保证外业精度的独立性,选用的控制点要与原测量区域的控制点不同,且重新采用一套设备及测量人员进行外业精度检测。选用6个检测点与4个未知点独立测量,构成同步观测GPS平面网,检测点与未知点的分布如图3所示。按照四等水准测量要求,结合GPS观测数据与检测点水准测量数据,获得水准测量观测成果。

图3 外业精度检测点分布图
6个外业精度检测点的成果如表1所示。从表1可知,二次曲面模型转换后的高程误差较低,最大值为0.042 m。根据公式(1)~(3)计算出外业精度检测的误差容许值为±5.44 cm,与二次曲面模型拟合误差最大值相比,最大差值小于容许值,表明外业检测结果符合相关要求。为进一步得到二次曲面模型的表达式,采用 Matlab编程算法对参数进行反演,获得参数最优结果,二次曲面数为公式(3)。经过对各个模型的内符合精度验算及外业精度检测,可以得出结论:本项目区域,采用二次曲面模型进行 GPS水准高程转换较为科学合理。
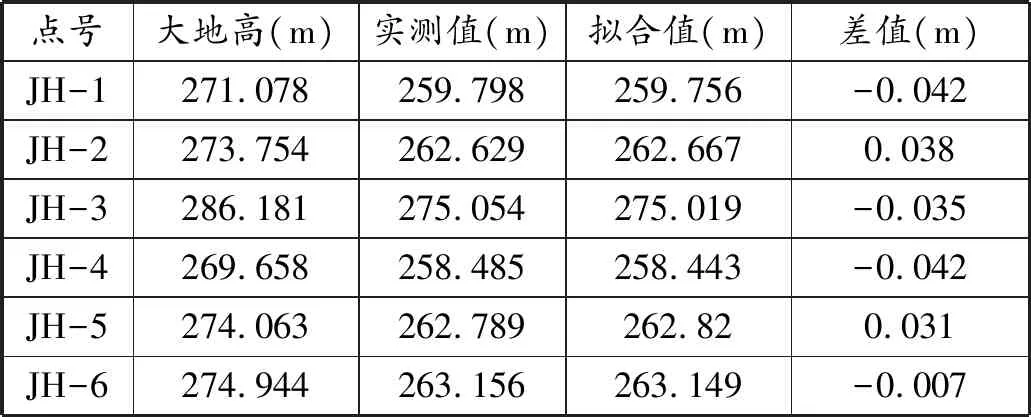
d=H水准-﹙HGPS-δ) (1)
3 结语
通过对项目区域 8个GPS水准高程模型的内符合精度参数对比分析,得出结论:二次曲面模型的中误差、最大残差及最小残差值均为最小,二次曲面模型残差分布范围更为稳定,残差值在3 cm以内的控制点占比超过90%。基于外业精度检测,获得二次曲面模型的最大误差值为0.042 m,低于容许值,最终确定项目区域采用二次曲面模型进行高程转换较为科学合理。
