郑州市东风渠水环境质量的GM(1,1)模型预测

张二丽，王玉龙，汪太行，冯 宇

（郑州财经学院信息工程学院，河南郑州450044）

本文基于时间段在2018.10-2019.9 之间郑州市东风渠流入七里河处的水资源监测数据[2]，同时选取pH 值、氨氮、总磷3项指标分别建立灰色GM(1,1)预测模型，并将预测数据与实际检测数据进行比较，检测灰色GM(1,1)预测模型对东风渠水环境质量的预测效果，以期为东风渠水体污染治理、污染防治、生态安全等问题提供理论支撑.

1 灰色GM(1,1)模型的建立

设离散原始数列为x(0)=(x(0)(1),x(0)(2),…,x(0)(n) )，通过对x(0)数列进行累加，产生新的数列x(1)=( )

x(1)(1),x(1)(2),…,x(1)(n) .

由x(0)数列构建的灰色GM(1,1)模型的微分方程为：

其中a为发展系数、b为灰色作用量. 该模型的时间响应方程为

理念决定行为。教师的理念是学生的起跑线。“以生为本”的教育理念是实现学生全面发展的坚固基石。这就要求教师必须坚守“让每个学生都成才，让每个学生都成人”的教育目标，必须坚持“每个学生都是独一无二的”理性思维，必须遵循“学生身心发展和认知有差异”的科学规律，切实提高自身的核心素养和综合能力，时时事事给学生以积极的引导，真正成为学生“学生锤炼品格的引路人、学习知识的引路人、创新思维的引路人、奉献祖国的引路人”，切实促进学生的全面发展，实现每个学生的综合素养都得到发展。

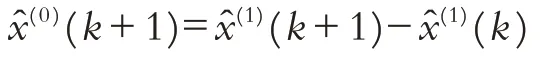
2 灰色GM(1,1)模型误差的检验及修正

2.1 相对误差检验法

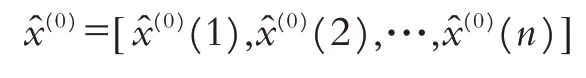
得到的残差为：

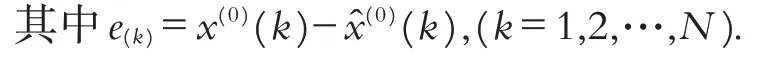
得到的相对误差及平均相对误差分别为：

2.2 残差GM(1,1)模型

当灰色GM(1,1)模型预测的精度过低或不满足预测模型的要求时，可通过残差序列建立一个新的GM(1,1)模型，对原来的模型进行修正，以此来提高模型预测精度.

假设ε(0)=(ε(0)(1),ε(0)(2),…,ε(0)(n))为x(1)的残差序列，其中ε(k)=x(1)(k)-x^(1)(k). 若存在k0，当n-k0≥4，则建模残差尾段为：

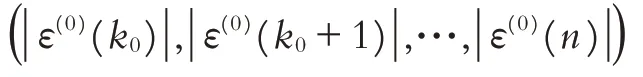
记作

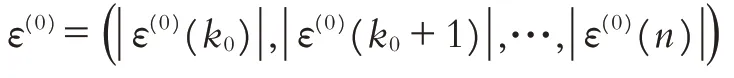
其一次累加序列为：

则残差模型的时间响应式为：

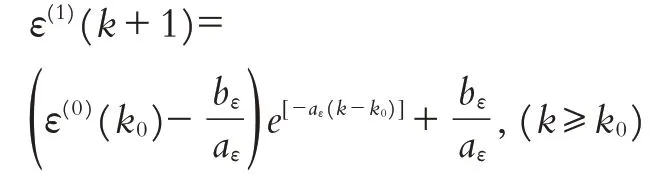
残差尾段的模拟序列为：

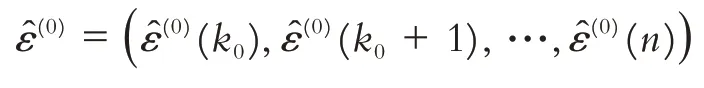
其中

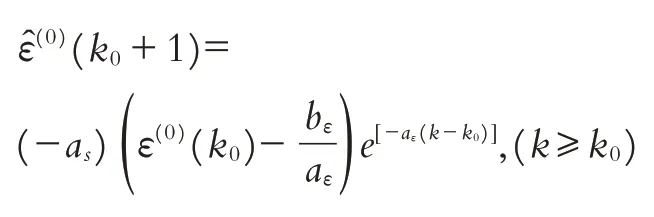
累减还原式GM残差修正模型时间响应式为：

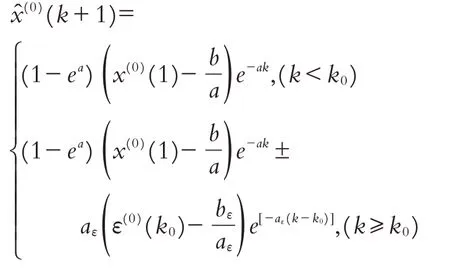
3 灰色GM(1,1)模型在东风渠水质预测中的应用

以2018.10-2019.9 郑州市东风渠流入七里河处水质检测数据为研究对象，选取pH值、氨氮、总磷三类指标监测的数据（见表1），采用灰色GM(1,1)模型对郑州东风渠水质进行预测[7-9].

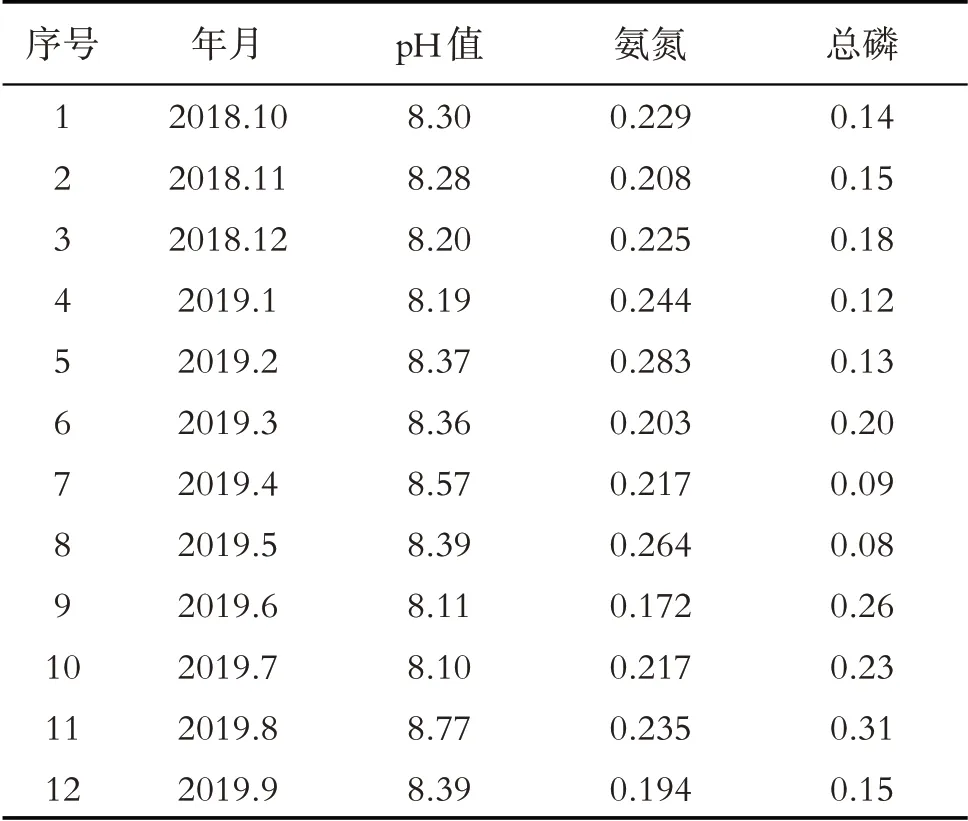
表1 2018.10-2019.9东风渠流入七里河处监测数据

3.1 东风渠pH值预测模型

以东风渠2018.10-2019.7 的pH 值监测数据作为模型的数据样本，建立GM(1,1)模型. 首先将数据样本作为原始序列，即x0=(8.30,8.28,8.20,8.19,8.37,8.36,8.57,8.39,8.11,8.10)，然后对x0进行一次累加得x0=(8.30,16.58,24.78,32.97,41.34,49.70,58.27,66.66,74.77,82.87). 通过GM(1,1)模型计算出发展系数a和灰色作用量b为a= 0.001，b=8.321，并建立GM(1,1)微分方程模型对GM(1,1)微分方程求解得到时间响应序列模型：

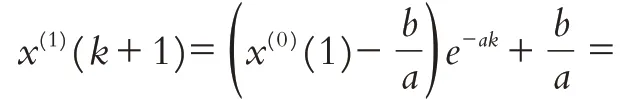
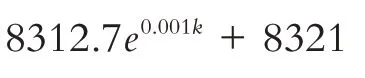
pH 值的模拟数据与实际数据比较如表2 所示，pH值数据拟合曲线如图1所示.

表2 2018.10-2019.7东风渠pH值模拟数据与实际数据比较

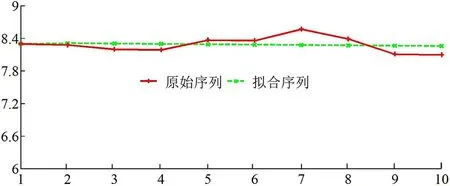
图1 pH数据拟合曲线

通过计算2018.10-2019.7 月东风渠pH 值10 个模拟数据的相对模拟误差的平均值得到平均相对误差为1.500%，其相对精度为98.500%. 故可利用建立的pH 值灰色GM(1,1)模型对2019 年8-9 月的pH 值进行预测，并与实际监测数据对比(见表3)，可见其相对模拟误差最小值为0.52%，最大为4.05%，表明模型准确地预测了东风渠流入七里河的pH值变化.

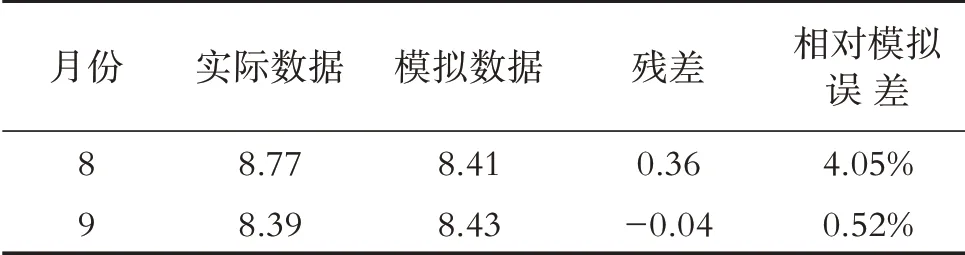
表3 2019年8-9月东风渠pH值模拟数据与实际数据比较

3.2 东风渠氨氮预测模型

以东风渠2018.10-2019.7 的氨氮监测数据作为模型的数据样本，建立GM(1,1)模型. 首先把数据样本作为原始序列，即：x1=(0.229,0.208,0.225,0.244,0.283,0.203,0.217,0.264,0.172,0.217)，对x1一次累加得x1=(0.229,0.437,0.662,0.906,1.189,1.392,1.609,1.873,2.045,2.262). 通过GM(1,1)模型计算出发展系数a和灰色作用量b为：a=0.010，b=0.239，并建立GM(1,1)微分方程模型对灰色序列微分方程求解得到模型：

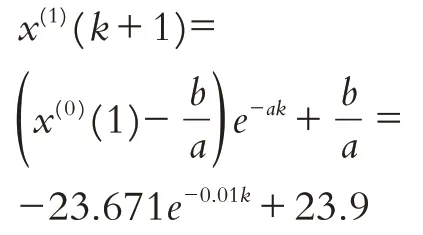
东风渠的氨氮模拟数据与实际数据比较如表4所示，氨氮数据拟合曲线如图2所示.

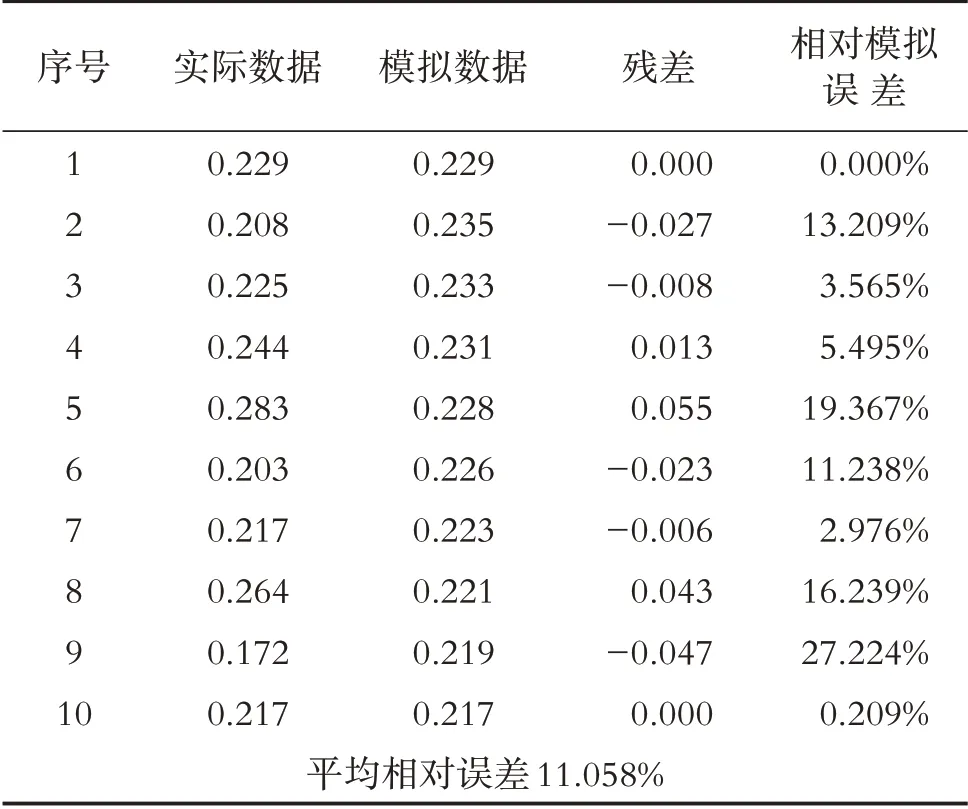
表4 2018.10-2019.7东风渠氨氮模拟数据与实际数据比较

通过计算2018.10-2019.7东风渠氨氮10个模拟数据的相对模拟误差的平均值，得到平均相对误差为11.058%，其相对精度为88.942%. 故可利用建立的氨氮灰色GM(1,1)模型对2019 年8-9 月的氨氮进行预测，并与实际监测数据对比(见表5)，可见其相对模拟误差最小为8.798%，最大为9.301%，说明模型较好地预测了东风渠流入七里河的氨氮量.

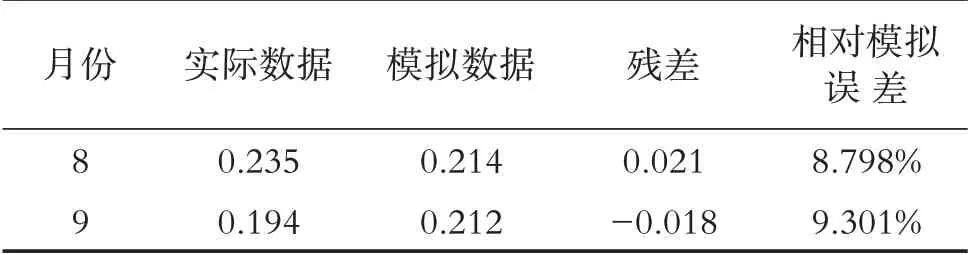
表5 2019年8-9月东风渠氨氮模拟数据与实际数据比较

3.3 东风渠总磷预测模型

以东风渠2018.10-2019.7 总磷的监测数据作为模型的数据样本，建立GM(1,1)模型. 将数据样本作为原始序列：x2=(0.14,0.15,0.18,0.12,0.13,0.20,0.09,0.08,0.26,0.23). 对x2一次累加得x2=(0.14,0.29,0.47,0.59,0.72,0.92,1.01,1.09,1.35,1.58). 通过GM(1,1)模型计算出发展系数a和灰色作用量b为：a=-0.053，b=0.117. 并建立GM(1,1)微分方程模型0.053x(1)=0.117. 对灰色序列微分方程求解得到模型：

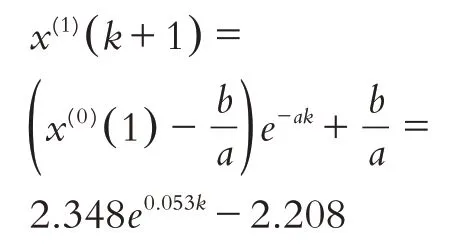
东风渠总磷模拟数据与实际数据的比较如表6所示，总磷数据拟合曲线如图3所示.

表6 2018.10-2019.7东风渠总磷模拟数据与实际数据比较

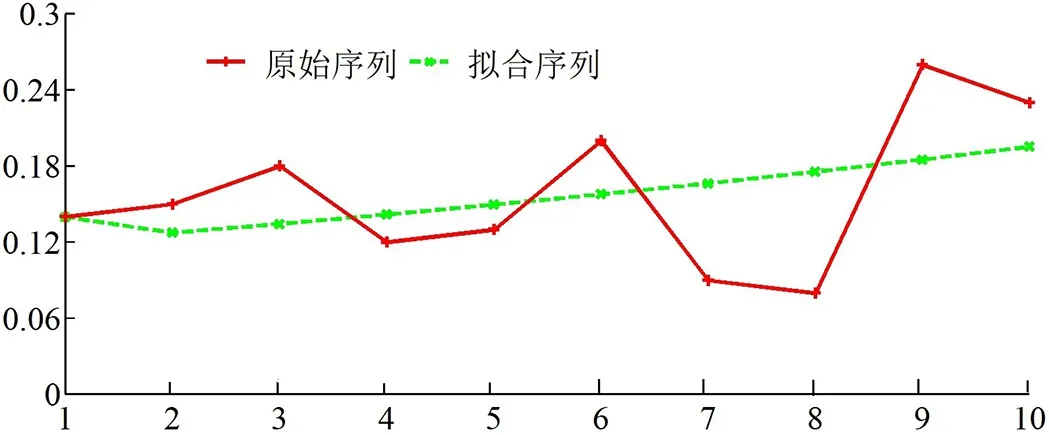
图3 总磷数据拟合曲线

通过计算2018.10-2019.7东风渠总磷10个模拟数据的相对模拟误差的平均值得到平均相对误差为38.123%，其相对精度为61.877%. 可通过残差GM(1,1)模型对误差进行修正以提高相对精度. 残差序列建模后的发展系数和灰色作用量a=0.175、b=0.106，所得到的时间响应方程为：

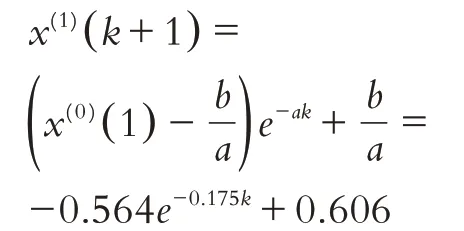
对表6 中总磷模拟数据与实际数据的残差数据取绝对值，据此得到东风渠总磷数据的残差修正拟合结果（见表7）.

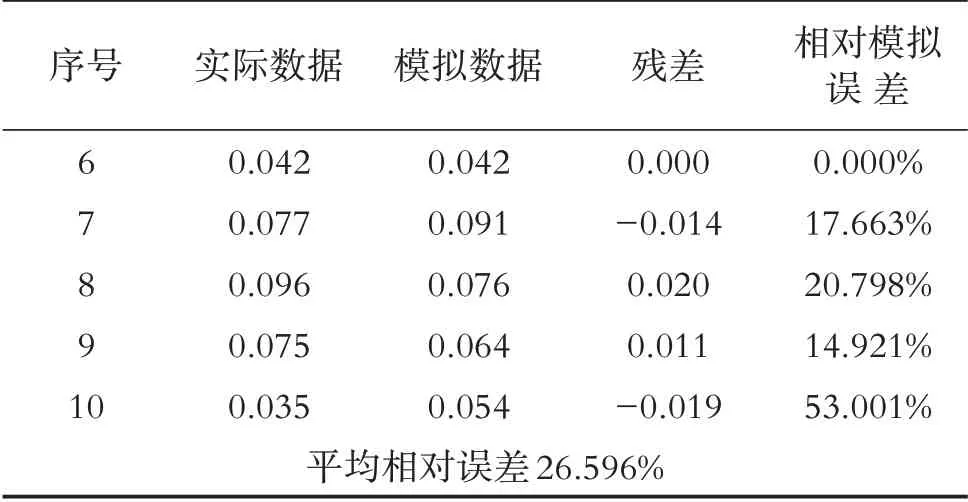
表7 2019年3-7月东风渠总磷残差修正拟合结果

通过计算2019 年3-7 月东风渠总磷残差的5 个相对模拟误差的平均值得到平均相对误差为26.596%，其相对精度为73.404%.故可利用建立的总磷残差GM(1,1)模型对2019 年8 至9 月的总磷进行预测，并与实际检测数据比较(见表8)，其相对模拟误差最小为18.956%，最大为32.253%，说明模型可对东风渠流入七里河的总磷进行预测.

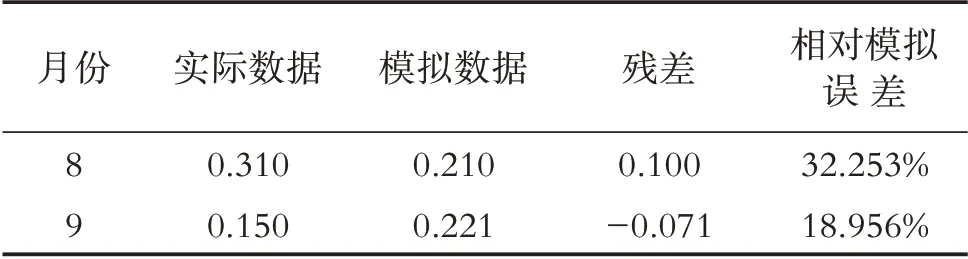
表8 2019年8-9月东风渠总磷模拟数据与实际数据比较

4 结语

本文利用灰色数学理论，在2018.10-2019.9 东风渠流入七里河处水质监测数据的基础上，选取pH值、氨氮、总磷三项指标，建立用于水质预测的灰色GM(1,1)模型. 由于所选取的水质指标监测数据波动范围较大，通过相对误差法对总磷的预测精度进行分析，结果发现预测精度相对较差，因此对模型进行改进，并利用改进后的残差GM(1,1)模型对2019年8 月和9 月的总磷进行预测. 结果显示pH 值灰色GM(1,1)模型预测精度为98.500%，氨氮灰色GM(1,1) 模型预测精度为88.942%，总磷残差GM(1,1)模型预测精度为73.404%，与实际监测的数据进行比较误差较小，印证了灰色GM(1,1)模型适用于东风渠水质的预测.

郑州市东风渠水环境质量对于郑州市区域经济的发展至关重要，通过GM(1,1)灰色预测模型对郑州市东风渠水质中pH、氨氮、总磷三类指标的合理预测可以为郑州市生态环境局提供科学依据，一定程度上对于制定水环境保护的相关政策法规具有参考价值[10].