高温作业专用服装温度变化的数学原理及其应用

卢 鹏，徐昌贵

（西南交通大学数学学院，四川成都610031）

人们在高温环境下工作时，需要穿着专用服装以免灼伤.专用服装由三层织物材料构成，即I、II、III层，其中I 层与外界环境接触，III 层与皮肤之间还存在空隙，记为IV 层.在设计专用服装时，为了降低研发成本、缩短研发周期，将体内温度控制在37°C 的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度. 专用服装材料的一些参数值如表1 所示.对环境温度为75 °C，工作时间为90 分钟的情形开展实验，测量得到假人皮肤外侧的温度（见表2，完成数据可查文献[1]）. 本文首先对环境―人体―服装传热的物理过程进行推理和分析，综合传热学知识[2-3]将服装导热过程简化为一维平板热传导模式，接着用微元法[4]推导出一维热传导偏微分方程，然后从材料的均匀性得到了不同材料在分界面处温度连续、热量连续等条件，并根据实验要求确定初始条件和边值条件，由此建立了在稳定环境中专用服装热传导的偏微分方程组模型. 通过对模型进行求解[5-7]，得出每层传播的规律. 最后对结果进行了验证，以期可用于指导服装的生产与研制.

表1 专用服装材料的参数值

表2 假人皮肤外侧的测量温度

1 问题分析

1.1 一维化思想的分析

由于热量在传递过程中，最终热量的对外表现形式为温度场函数T(x,y,z,t)，而在本文中，高温防护服装材料的各处均在进行热量的传导，对任意一个热量微元，由于材料各向分布均匀，即各个热元传热的速度是互相协调的，因此微元在垂直向的热量变化是相同的，即在图1 中Y方向上温度处处相同，由此可以认为热量是沿一个方向传递，热元的侧面之间没有进行热量交换，即二维温度分布可进一步表示为T(x,t)，即温度为时间和单维度位置变量的函数.

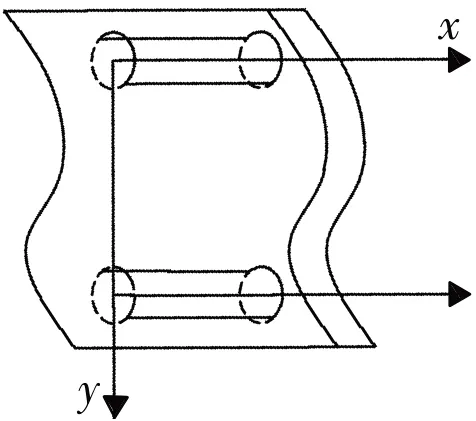
图1 热量微元的选取示意图

1.2 一维热传导方程的推导

（1）热量流动速率的确定

在对服装材料上任意位置取一个某种材料的圆柱体微元，该材料微元的横截面均匀且材质相同，热量只能沿某特定方向进行流动，此处方向约定为x轴方向. 根据经验原则，在某时刻t，通过点x横截面上的单位面积热流动速率为[8]：

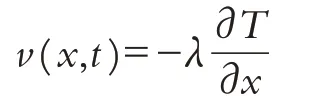
其中：λ为该材料的热传导率，v(x,t)为热流速率.

图2是热量流入材料微元的示意图.

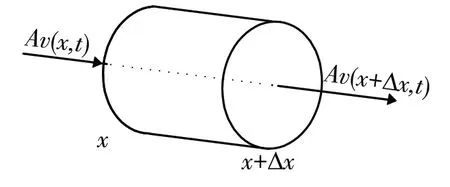
图2 热量流入材料微元的示意图

由图2可知，通过两个端面的热量流动速率为：

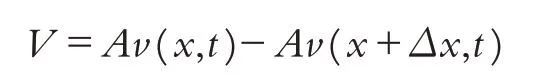
将v(x,t)代入得：

（2）单种材料微元吸收的热量[9-10]

把该材料圆柱微元温度从0 加热到T所需的热量为：

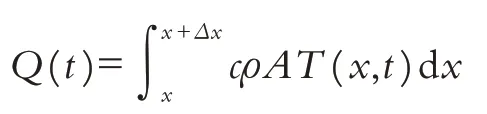
对上式两边进行微分并应用积分中值定理有：

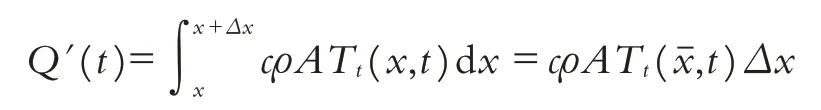
其中为x与x+Δx之间中的某个值.

（3）一维热传导方程的确定

Q(t)表示把圆柱微元对应于x与x+Δx的一小段温度从0 度升到已知温度T(x,t)所需的热量，又因为热流仅从端面进出，由此根据V=dQ/dt和热量流动V表达式得：

基于上述两种不同的热量速度推导方法得出的V相等，于是有：

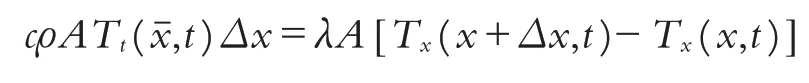
所以，可以得出

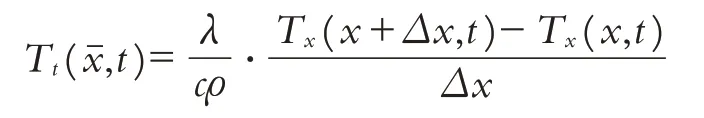
令Δx→0，即xˉ→x，可以得到热量的一维传导方程：

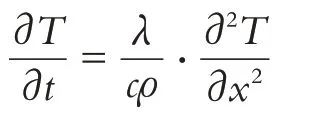
2 模型建立

2.1 坐标系建立及热量传递机理分析

在忽略沿假人皮肤平面方向导热的条件下，可把皮肤内的导热问题认为是无限大平板问题，即一维导热问题. 由题目可知，在高温下工作的人体皮肤温度必须在一定的范围内，人体才能正常工作，而人体皮肤温度升高是由于环境温度向内传递，才不断导致温度越来越高，而高温防护服的特点就在于能够有效地减少热量向人体传递，控制服装内部的温度，维持人体舒适温度，而热量向内传递是一个逐步传递过程，通过一层层防护服材料的过程.

建立如图3 所示坐标系，根据前述分析，坐标系的两个维度为材料的位置坐标和时间. 温度分布是坐标位置和时间的二维函数，坐标轴的原点位置及热量传递过程如图3所示.

图3 热量传递过程示意图

2.2 各织物材料层内一维热传导偏微分方程的建立

热量在特定的某种材料中传递符合一维热传导规律，由此，建立任意层中热量传递的偏微分方程.第i层织物材料中的一维热传导偏微分方程为：

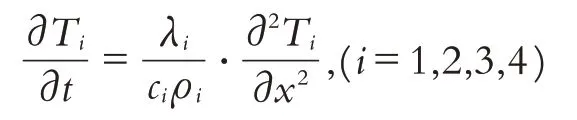
其中：Ti是第i层织物材料中的温度场函数，为二元函数Ti(x,t)，x是织物材料在厚度方向的位置坐标.

2.3 各织物材料在分界面处传导模式分析

能量在同种介质中按照一维热传导偏微分方程的递变规律进行传递，根据热量传递的连续性特征可知，温度向下传递时，在分界面上二者的温度应该相等，则有如下等式：

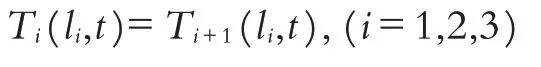
同时在交界面处热流密度也是连续变化的，从而有如下等式：

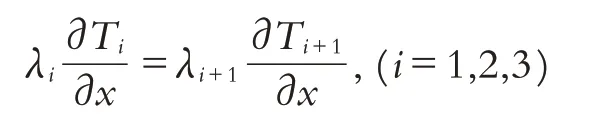
2.4 边值条件的确定

由高温防护服的工作环境可知，服装最外层面料是直接暴露在空气中的，最里层即第IV 层空隙与人体皮肤接触，因此在温度场函数中，当位置坐标确定后有如下边界条件：

（ⅰ）织物材料层的左边界条件：T1(0,t)=T0.

（ⅱ）织物材料层的右边界条件：T4(l4,t)=T5.

其中：T0=75 ℃为外界环境的温度；T5为人体皮肤外侧温度且数据由表2 给出；di表示第i层织物材料的厚度，li表示前i层织物材料的厚度和，即l4=d1+d2+d3+d4.

2.5 初值条件的确定

高温防护服装在进入实验室之前，应该长期处于一个稳定环境场中，同时由于假人体内温度一直控制为37 ℃，故有初值条件为：

2.6 偏微分方程组模型的建立

基于上述热量传递的分析过程以及相关的定解条件，可以建立起整个热量传导的正向偏微分方程组模型：

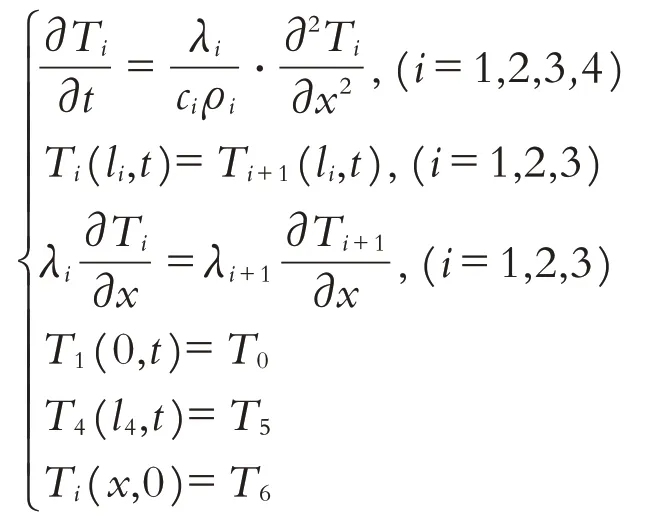
3 模型求解

在偏微分方程领域，这是一个一维抛物型方程，考虑到定解条件中既包含开始时刻织物材料层温度分布的初始条件，又包含织物材料层温度分布的边值条件. 因此，这是一个一维热传导混合问题[11]. 由于混合问题的求解过程往往是比较复杂的，有时很难有解析解. 即使该一维热传导混合问题的解析解可以求出，其解的形式也通常是一个无穷级数形式，不易于对外界环境―服装―人体整个系统热量传导及温度变化过程进行分析. 因此，本文利用有限差分法对该偏微分方程组进行求解.

采用一定的网格划分离散化温度场，把实际连续的温度场离散为有限数量的点. 用这些点上的温度值近似描述连续的温度场. 针对x-t平面，取Δx和Δt分别为x方向和t方向的步长，分别做一组平行于x轴和平行于t轴的直线，将x坐标等分为N份，将t坐标等分为M份. 则坐标可表示为(kΔx,jΔt)(k=1,2,…,N;j=1,2,…,M)的网格点，简记为(k,j)，网格上每个格点对应一个温度，则Ti(x,t)在此格点上的取值记为Ti(k,j)，如图4所示.

图4 网格划分示意图

3.1 显式差分算法

用二阶中心差分近似代替温度分布函数对空间的偏微分，即

用向前差分近似代替温度分布函数对时间的偏微分，即

根据上述建立的差分格式，可将该偏微分方程改写为：

化简为：

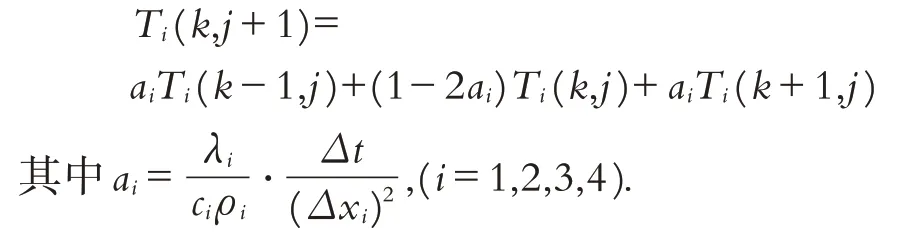
算法的计算过程是由Ti(k-1,j)、Ti(k,j)、Ti(k+1,j)三个点去计算Ti(k,j+1)，具体如图5所示：

图5 显式差分格式

这样根据上面公式，每次算完一行以后往上迭代就可以算出网格中所有点的值. 但需要注意是总共有四层，每层的ai取值不同；显式方法在时，为数值稳定且收敛；所以在时间步长与位移步长取值时需要满足条件；为了满足收敛，每个部分的步长有可能不同；材料分界面上的网格节点(k,j)使用下面方程进行计算（温度相等，热量相等）：

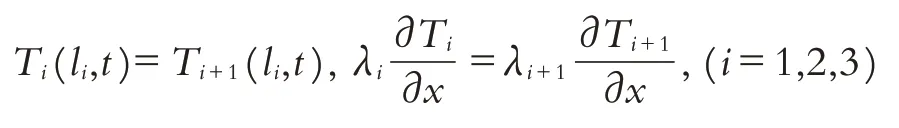
离散化第二个方程，化简可得

其中νi=λi/Δxi.

若要用显式方式求解，时间步长要取为0.01 s，位移步长I、II、III层取为0.1 mm，IV 层取为1 mm，再按照上述公式计算可得结果.

3.2 隐式差分算法

用二阶中心差分近似代替温度分布函数对空间的偏微分，即

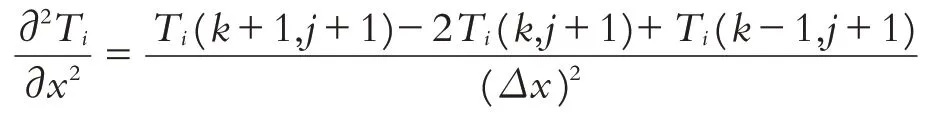
用向后差分近似代替温度分布函数对时间的偏微分，即

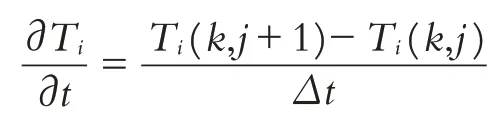
根据上述建立的差分格式，可将该偏微分方程改写为：

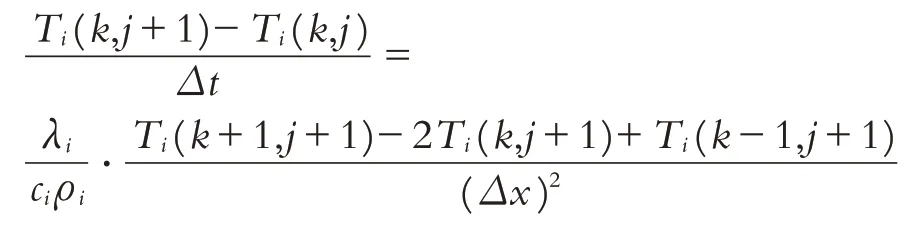
化简为：

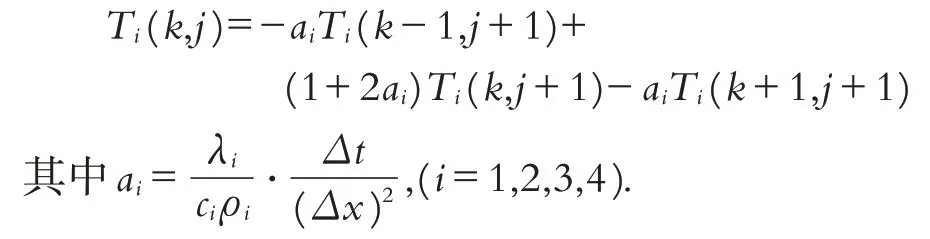
计算过程是由Ti(k-1,j+1)、Ti(k,j+1)、Ti(k+1,j+1)与Ti(k,j)建立一个线性方程组进行计算，具体如图6所示：

图6 隐式差分格式

根据上面公式，每次求解一个联立线性方程组后，再往上迭代就可以算出网格中所有点的值. 具体如下：

第一步：当j=0 时求解如下线性方程组，得出Ti(k,1)(i,=1,2,3,4;k=1,2,…,N-1)：

其中：

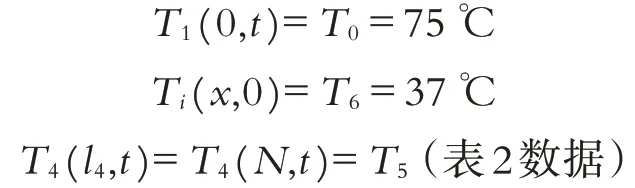
若规模较大的线性方程组直接采用高斯消元法求解，对于微型计算机来说运算量与存储量难以承受，本文根据方程组系数矩阵的特点，采用追赶法（需要满足一定条件，本题已满足）求解，大大节省了计算时间.

第二步：当j=1,2,…,M-1 时求解M-1 个线性方程组，得出所有Ti.

需要注意的是总共有四层，每层的ai取值不同，在求解线性方程组时注意边界条件；隐式方法不论ai的大小，都数值稳定且收敛，但计算量会较显式方法要大，因为每前进一个时间间隔，就需要求解一个联立的线性方程组；方法本身收敛，每个部分在取步长时可以相同，即Δx=Δxi；材料分界面上的网格节点(k,j)由下面方程给出：

离散化第二个方程，化简可得

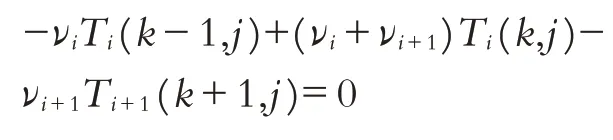
其中νi=λi/Δxi.

3.3 结果说明

为了计算方便及稳定，采用隐式差分算法进行计算，时间步长取为1 s，四层的位移步长都取为0.1 mm. MATLAB 软件[12]编程计算偏微分方程组即可得到温度分布数据表格（表3）.

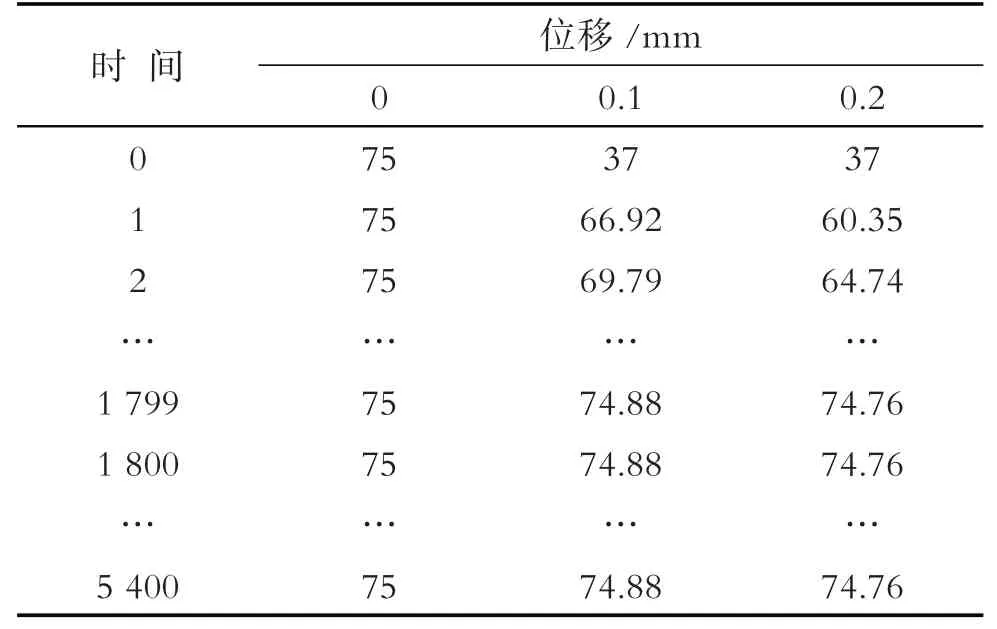
表3 部分温度分布数据

温度分布函数Ti(x,t)是时间参数t和空间参数x的二元函数，绘制温度分布三维图（图7）.由图7可见，初始时刻服装材料各处温度均为37 ℃. 假人进入实验室高温环境后，服装材料温度迅速上升，其中I层材料温度变化幅度最大，因为其与外界环境直接接触. 针对同一时间，随着坐标位置的增加，节点处温度上升幅度逐渐减小；针对同一节点，随着时间增加，该节点处温度逐渐上升，但温度变化率逐渐降低，最后所有的节点温度趋于某一稳定温度值.

图7 温度分布三维图

图8 反映了不同时刻下织物材料内部温度的变化. 由图8 可以看出，随着时间的增加，各个位置处网格节点的温度在逐渐趋于稳定，即热传递达到了稳定状态；且在稳定状态下，各个网格节点的温度随位置坐标呈线性变化.

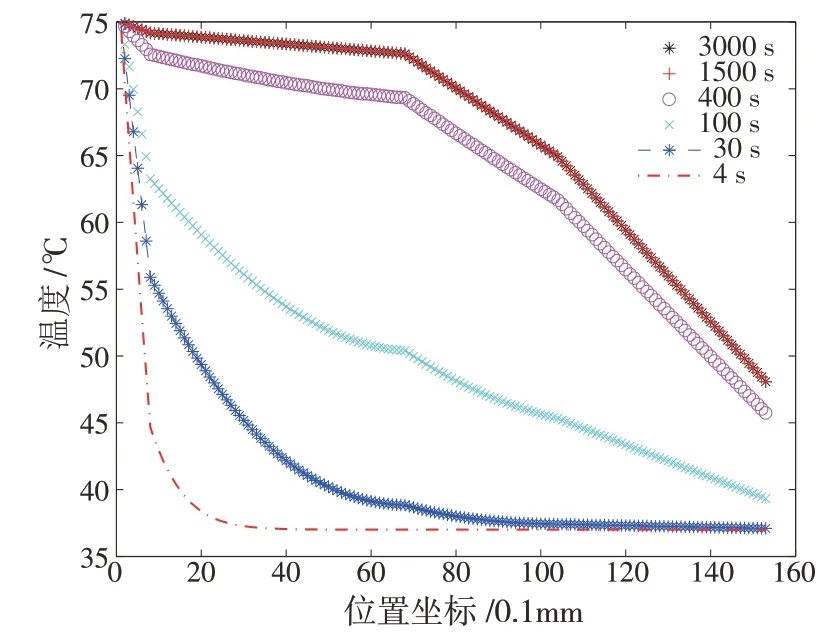
图8 不同时刻下织物材料内部温度的变化

图9 的分界面处织物材料温度随时间的变化表明，位于分界处的网格节点，随着时间的增加，这些节点上的温度均有一个快速增长的过程，但在该过程中温度变化的速率逐渐变缓，最后，节点上的温度都达到了稳定状态.

图9 分界面处织物材料温度随时间的变化

4 模型验证

由表2数据和图9可以发现，当假人放入稳定的环境中，从1 645 s以后温度的变化将趋于稳定，这个时候温度和时间就没有关系了，只和位移有关系.故可以建立稳定状态下的数学模型，并用来检验非稳态模型所算出的结果.

稳定状态下的数学模型如下：

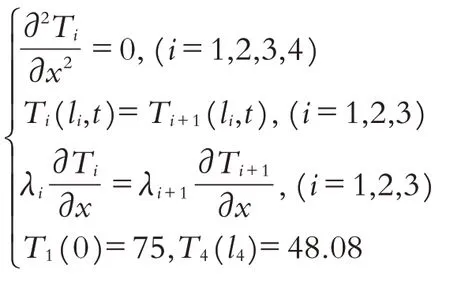
求解可得：

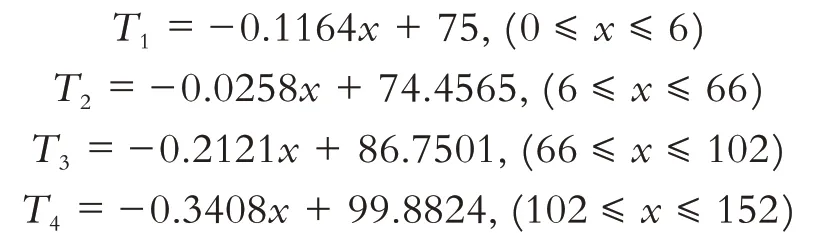
由原模型计算可知，当1 645 s后温度趋于稳定，表4 给出了稳定状态和原模型1 645 s后不同位置上的温度，同时也给出了两种结果的散点图（图10）.从表4 和图10 可以看出，两种方式的计算结果几乎没有差别，所以本文所建立的偏微分方程组模型以及求解的结果是正确的.

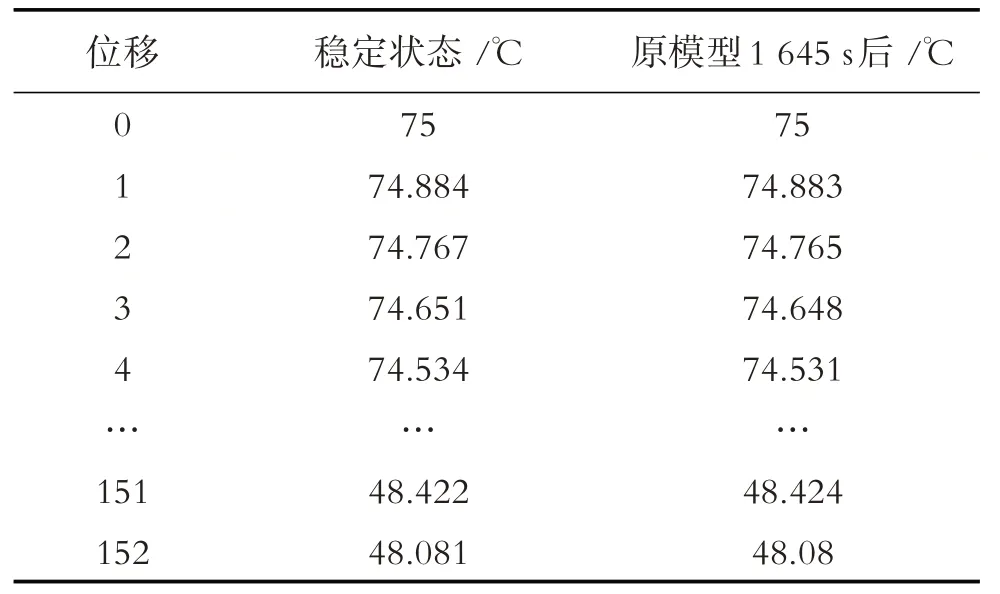
表4 两种模型温度结果对比

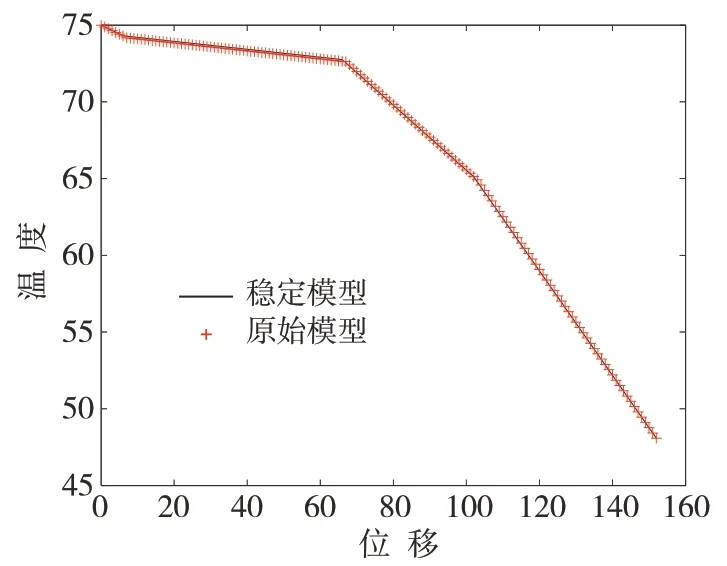
图10 两种模型的温度变化曲线

5 结语

本文建立了在稳定环境中专用服装热传导的偏微分方程组模型，由此可以掌握温度变化的规律，同时改变材料中的某些参数值，运用模型和算法可得更多温度变化的结果，对这些结果进行研究与分析，可以为生产专用服装的科研人员提供参考，以使其降低研发成本，提高制作工艺.