基于流体置换理论的致密砂岩气层识别方法研究
2020-07-14王文文
王文文
( 中海油田服务股份有限公司油田技术事业部 ,北京 101149)
鄂尔多斯盆地东缘F区块主要勘探层位为上晚古生代地层,自上而下发育二叠系石千峰、上石盒子、下石盒子、山西、太原组及石炭系本溪组,其岩性主要为砂岩、泥岩、灰岩及煤。经过数年勘探,区块致密砂岩气已取得了一定成果。但在致密砂岩储层勘探开发过程中,由于致密砂岩储层致密储层孔喉半径小,非均质性强,导致“非阿尔奇响应”,使得致密储层油气水层电阻率基本相当,高阻水层和低阻气层的普遍发育,造成流体性质识别难度大,含气性评价问题日益凸显。
针对致密气储层流体识别难点,前人应用常规、阵列声波、核磁等测井资料,评价致密砂岩储层流体性质,提出了诸多方法,取得了一定效果。吴松涛等[1]利用核磁等资料揭示了致密储层可动流体饱和度分布特征,明确了致密砂岩储层微观孔隙结构与可动流体的关系;吕斯端等[2]分析了致密鄂尔多斯盆地延长组致密储层的测井响应特征,认为致密砂岩气藏随着含气性的降低,电阻率边界并不明确,常规电阻率与声波时差图法区分致密气,易出现混合现象;杨克兵等[3]提出了纵横波波速比-纵波时差曲线重叠方法、泊松比-体积模量曲线重叠方法进行致密砂岩储层含气性定性评价;对鄂尔多斯盆地致密储层特征、测井敏感性的分析,初步实现了储层流体性质的定性划分,但当储层岩性、泥质含量发生变化时都会对识别效果结果造成改变,说明上述评价方法还存在局限。
下面以鄂尔多斯盆地东缘上古生界致密砂岩气层为例,以地震中的Gassmann理论为基础,分析致密储层含气性与岩石力学参数的关系,应用阵列声波资料,获取表征储层含气性的流体模量参数,提升致密砂岩储层流体识别符合率。
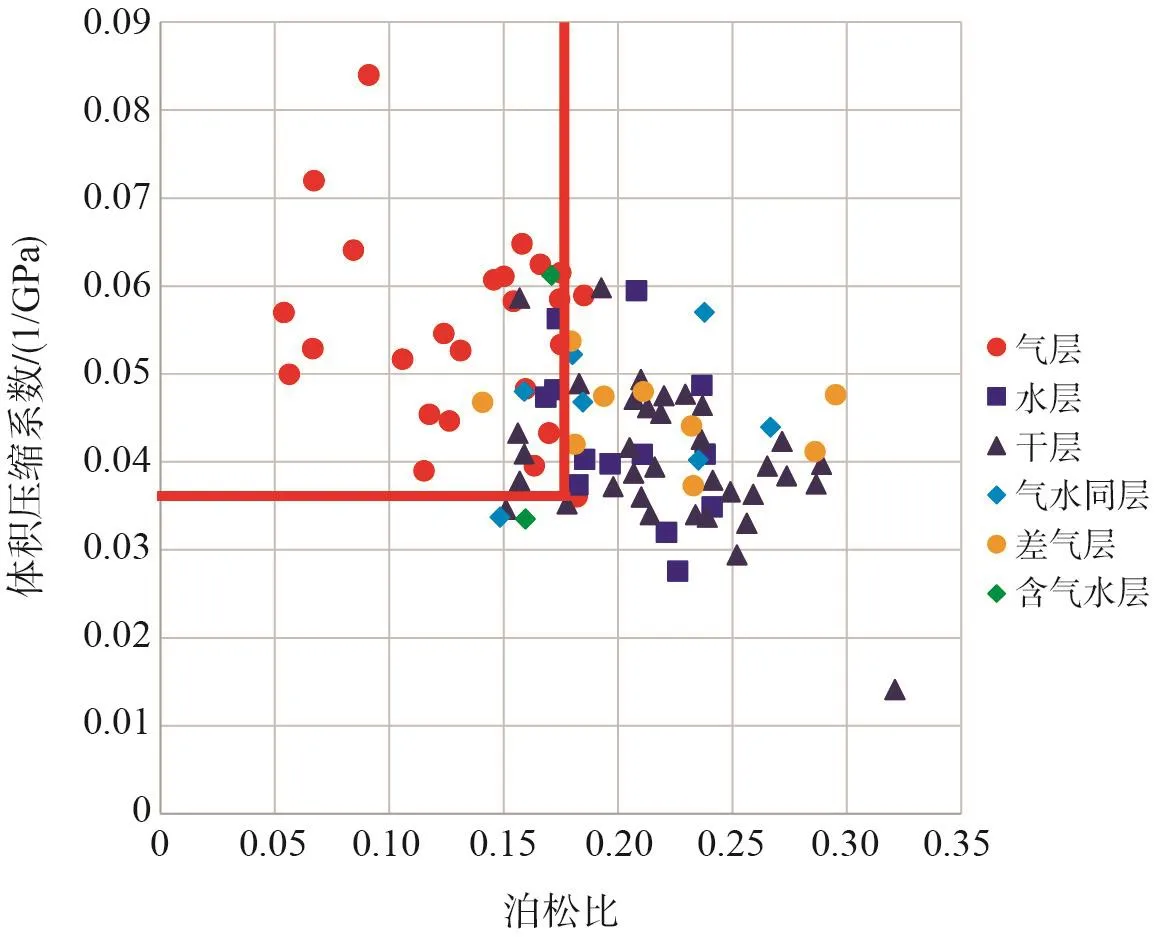
图1 泊松比与体积压缩系数交会图
1 致密储层含气性与岩石力学参数关系
储层含气后,造成纵波速度降低,因横波不受流体影响,横波速度不变;与纯水层相比,含气储层的纵横波速度比降低;同时不同流体的压缩系数差异较大,气体压缩系数相对较大,而水压缩系数小。基于上述力学参数特性可以定性识别气层。
利用图版法对B区块有试气资料的层位进行统计,结合测试产气量和产水量对测试结论进行分类,分别建立了泊松比与体积压缩系数(图1)、纵横波速度比与敏感参数、杨氏模量与体积模量(图2)、纵横波速度比与拉梅系数图版(图3)。
由图1泊松比与体积压缩系数交会可知,测试结论分别为气层、差气层、干层、气水同层、含气水层、水层,将对应层位上的数据点投影到图版上,该图版可以对气层与非气层具有区分的作用,但部分水层与气层点混杂。
通过图2、图3可知,利用不同模量参数交会均对气层与非气层具有区分作用,但仍存在部分水层与气层的混杂。
由于常规岩石力学参数受骨架、泥质及孔隙流体的多重因素影响,因此剥离泥质及骨架影响,直接获取孔隙流体模量参数,将有效提升流体识别精度。
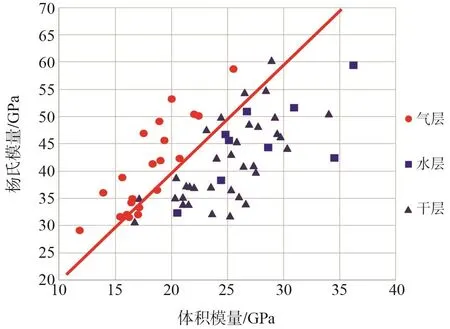
图2 杨氏模量与体积模量交会图
2 流体置换方法原理
1951年Gassmann发表了著名的Gassmann方程[4],该项理论在物探领域应用广泛,它给出了岩石的干骨架、固体基质和孔隙流体的体积模量与岩石饱和不同组分孔隙流体的体积模量间的关系。Gassmann方程很大的用途在于流体替换模拟FRM(Fluid Replacement Modeling)。对于多相饱和岩石可以使用孔隙流体等效模量概念,通过使用Gassmann方程计算计算等效流体模量,从而进行流体性质判别。
随着岩石压缩性的增大,孔隙压力也随之增大。同时,孔隙压力的增加阻止了岩石的压缩,从而增强了岩石的刚度。低频Gassmann理论可以有效地预测不同流体饱和岩石有效体积模量:
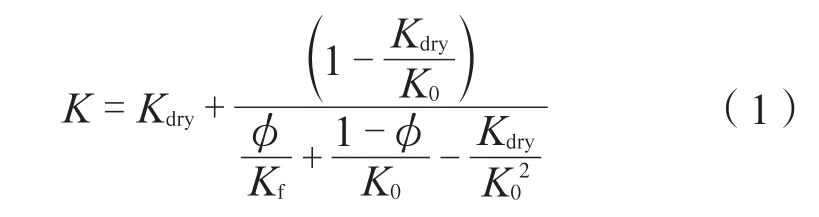
式中:K为岩石体积模量,Pa;Kdry为干岩石有效体积模量,Pa;K0为组成岩石的矿物有效体积模量,Pa;φ为孔隙度,小数;Kf为孔隙流体的等效体积模量,Pa。
Gassmann方程适用于完全弹性的岩石骨架结构和完全饱和的孔隙流体,对各种孔隙几何形态都具有普遍性和有效性。
通过计算岩石的体积模量、矿物的有效体积模量和干岩的有效体积模量,可以得到孔隙流体的等效体积模量。
2.1 岩石体积模量
基于速度在孔隙介质中的表达式,联立可求解岩石体积模量:
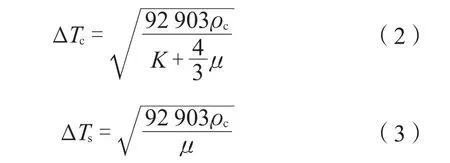
式中:ρc为岩石的密度,g/cm3;ΔTs为岩石的横波时差,m/s;ΔTc为岩石的纵波时差,m/s;μ为岩石的有效剪切模量,kPa。
2.2 VRH法获取矿物有效体积模量
岩石中矿物的有效体积模量可以用VRH法(Voigt Bounds , Reuss and Hill Average)获得。Voigt平均模型和Reuss平均模型分别代表混合物中平均应力和应变之比。Voigt模型假设各处应变相等(并联模型);Reuss模型描述了等应力条件 (串联模型),非常适用于悬浮物和流体的混合。Hill模型(1952年)为平均Voigt上限和Reuss下限,这就是VRH平均模型[5]:
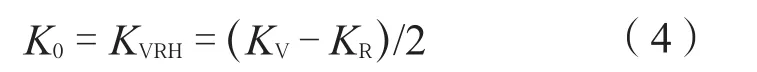
式中:KVRH为Hill模型求取的有效体积模量,Pa;KV为Voigt模型求取的有效体积模量上限值,Pa;KR为Reuss模型求取的有效体积模量下限值,Pa。
2.2 干燥岩石有效体积模量的计算
干燥岩石的有效体积模量并不完全等同于气体饱和岩石的有效体积模量,只有当填充气体的体积模量接近于零时才是等效的。在正常的油气储层条件下,由于高温高压,气体具有较高的体积模量,也是满足饱和流体条件的。
干燥岩石的有效体积模量主要通过Greenberg-Castagna法、Biot系数法、干燥岩石泊松比法获得。Biot系数法作为一种简单快速的方法被广泛使用。
干燥岩石体积模量可以写为:

式中:Kdry为干燥岩石的有效体积模量,Pa;β为Biot系数,无量纲。
Biot系数一般被视为一种孔隙度的函数。Geertsma、Krief[6]等和Nur[7]等都给出了由孔隙度φ拟合Biot系数的经验性公式。
在纯砂岩,Geertsma与 Smit提出了应用的经验关系如下:
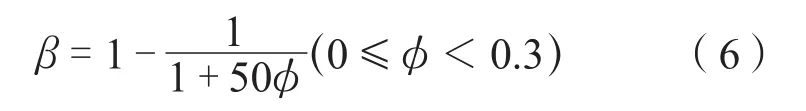
Krief认为Biot系数是一个连续的孔隙度函数:

3 应用实例
图4为A井利用流体置换理论识别致密砂岩气层的成果图。从图4中可以看出,29号层深度段1 478.5 ~ 1 481.3 m,层厚2.8 m,对应的自然伽马整体呈低值(局部受高放射性矿物影响),岩性较纯;井径曲线规则、井眼条件良好;深、浅侧向电阻率曲线呈现低阻、分异特征;阵列声波的泊松比和速度比具有微弱“镜像特征”;但流体模量呈现低值,数值低于1 MPa,利用流体模量反算含气饱和度较高,指示该层段为气层;该井1 478.5 ~ 1 481.3 m层段射孔,获得日产气无阻流量35 381 m3/d,为工业气流层,与解释结论完全符合。33号层深度段1 498.5 ~ 1 505.0 m,测井响应类似,呈现低阻特征,利用流体模量反算含气饱和度较高,指示该层段为气层。
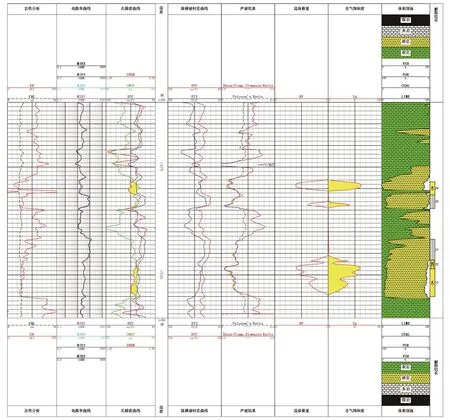
图4 A井流体置换理论识别致密砂岩气层的成果图
4 结论
(1)分析区域致密砂岩储层声学响应特征,发现纵横波速度比、泊松比等参数对含气变化响应敏感。通过多种力学参数交会,能够区分气层、差气层、干层、气水同层、含气水层、水层,但部分水层与气层点混杂。
(2)基于地震岩石物理Gassmann理论,结合阵列声波等测井数据,建立了包含岩石孔隙、骨架、混合流体的模量模型,最终获得混合流体模量。
(3)研究区测试井实例表明,典型致密砂岩低阻气层,电阻率及其他交会方法指示微弱,流体性质识别难度大。基于流体置换方法,利用流体模型识别气层,识别结果更为直观可靠。
