基于区域农业旱灾损失预测的混频GM(1,N)模型研究
2020-07-14罗党秦嘉欣
罗党, 秦嘉欣
(华北水利水电大学,河南 郑州450046)
21世纪以来,由于气候变化的影响,几乎每年在不同国家和地区都有极端旱灾发生,其中农业是受旱灾影响最严重的领域之一[1]。农业干旱是因外界环境因素或人类活动引起的农作物体内水分收支失衡而影响其正常生长的现象。农业旱灾是由农业干旱引起的,由于水源不足、抗旱经济条件有限等原因,人们不能及时采取补救措施以满足农作物生长的正常水分需要,最终造成较大的减产或绝产的现象。区域农业旱灾是由自然、经济、社会等诸多因素耦合作用的结果[2],农业旱灾直接引发的粮食减产,会造成严重的经济损失,甚至导致粮食安全危机等。且粮食产量与食物安全有密切关系,从宏观上来看,对宏观经济环境及政策制定也会产生深远影响;从微观上来看,对农民的生活有着重要影响。因此,进一步研究气象要素对粮食产量的影响,对保障粮食持续供给和维护地区稳定都有重要意义。
正是由于旱灾损失数据具有非常重要的影响力, 因而,众多学者对农作物旱灾损失进行预测,并努力提高预测精度。房世波[3]采用3 a滑动平均、5 a滑动平均和二次曲线3种方法模拟了5个地市的棉花趋势产量,并分析了各相似气候条件区域的气候产量的相关性,结果表明,气候因子对棉花的产量存在较大的影响。汤瑞琪等[4]运用非一致频率分析方法,对已有的中国旱灾损失数据进行频率分析,结果发现,旱灾损失序列呈现出比较明显的时序规律。张强等[5]利用中国农业干旱灾害的灾情资料,研究了气温和降雨量等气象因子对农业旱灾综合损失率的影响。王亚许等[6]利用APSIM模型分析了玉米的旱灾损失规律,评估了玉米旱灾风险等级,结果表明,辽宁省因旱损失严重,玉米因旱损失频率曲线大致呈现P-Ⅲ型概率分布。魏庆伟等[7]利用河南省浚县冬小麦单产数据,分别采用综合平均趋势法、HP滤波法等4种常用方法拟合了冬小麦趋势产量,并计算出对应的气象产量,结果表明,综合平均趋势法分离的趋势产量与实产变化趋势最为吻合,是分离冬小麦趋势产量与气象产量最准确的方法。罗靖[8]利用气温、降水量和粮食单产的数据对比分析了贵阳市粮食单产与气候的相互关系,研究发现,贵阳市气温对粮食产量存在负影响,粮食年产量与降水量增减趋势相同。胡家敏等[9]利用贵州省逐日气象数据与水稻产量数据,分析了典型干旱年份水稻不同生育期的累积干旱指数与减产率的关系,结果表明,利用不同生育期的累积干旱指数可以准确评估贵州各地水稻的干旱损失。邱爽等[10]利用滑动平均法、灰色关联度分析法,分析了气象灾害对西南四省市的粮食产量的影响。
灰色多变量预测作为灰色预测的一个重要分支,一直是国内外学者的研究重点,众多学者对多变量预测模型的基本形式及适用范围进行了拓展[11-16]。罗党等[17]建立了组合预测模型——BPSGM(0,N)模型,并将其应用于河南省新郑市土壤含水量的预测,基于降雨量、气温等气象因素建立了模型,并取得了良好的预测效果。刘呈玲等[18]利用弱化算子处理方法改进灰色GM(0,N)模型,并利用该模型预测了太湖流域用水总量,预测结果与流域水资源管理实施目标及水资源可持续利用战略需求基本相符。路璐等[19]计算了冬小麦生育期土壤水分和水文气象因子之间的灰色关联度,并根据冬小麦在不同时期土壤水分随水文气象因子的变化规律,构建了其不同生育期内的土壤水分计算模型。
传统的预测方法是选取与因旱灾导致的粮食产量损失同频率的年平均气象数据,但是在简单加权平均的过程中会造成大量信息损失。某年内可能发生多次不连续的干旱事件,最终的产量损失是多次干旱事件的累加结果,但一整年内并不全是作物的生长季,基于每年的历史数据无法探究作物在不同月份、不同生育期的灾损模型。因此,本文考虑在月尺度下探究因旱灾导致的粮食产量损失与气温、降水量等气象数据和有效灌溉面积之间的关系。针对因旱灾导致的粮食产量损失预测中高频气象要素与低频社会经济要素共存的特征,本文将传统的GM(1,N)模型推广至多变量系统中系统行为序列与相关因素序列采样频率不一致的情形,并利用2006—2017年安阳市因旱灾导致的粮食产量损失序列,构建混频数据的GM(1,N)模型,模拟粮食产量损失与气温、降水量等气象数据和有效灌溉面积之间的关系。
1 混频GM(1,N)模型构建及其求解
1.1 模型构建及参数估计
定义1设系统特征数据序列为:
相关因素序列为:



(1)
为混频GM(1,N)模型的基础形式,记为MFGM(1,N)。其中:
fj=(fj(1,ω1),fj(1,ω2),…,fj(1,ωmj),
fj(2,ω1),…,fj(n,ωmj))。
且对任意固定的t,有:
对任意固定的k,有:
fj(1,ωk)=fj(2,ωk)=…=fj(n,ωk)。

定义3称
(2)
为MFGM(1,N)模型基础形式的白化微分方程。
则矩阵形式的MFGM(1,N)模型为:
(3)
其中B=(b2,b3,…,bN) 。

(4)

1.2 混频GM(1,N)模型求解

L=
则参数列的最小二乘估计满足[20]:



证明将k=2,3,…,n代入MFGM(1,N)模型,得:
⋮
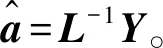
2)当n>N+1且L为列满秩矩阵时,有L的满秩分解为L=BC,进而可以得到L的广义逆矩阵为:
L-=CT(CCT)-1(BTB)-1BT。

由于L是满秩矩阵,C可以取单位矩阵,即L=BIN,L=B。则:
(BTB)-1BTY=(LTL)-1LTY。
3)当n CT(CCT)-1Y=LT(LLT)-1Y。 证毕。 定理2MFGM(1,N)模型白化方程的时间响应式为: 即: 证明利用常数变易法可以求得MFGM(1,N)模型的白化方程的解,令 (5) 假设Q(t)=0,则: (6) 式(6)的通解为: x(1)=ce-at。 其中c为任意常数,由于Q(t)不为0且具有式(5)的函数形式,则令 x(1)=c(t)e-at。 (7) 两边求导可得: 代入原方程可得: 两边求积分可得: 代入式(7)得: (8) 进一步可得: 证毕。 MFGM(1,N)模型中,权重函数fi(x)的主要功能是集结高频数据的大量信息,同时进行降噪。权重函数fi(x)的选择,要求其既保持形式多样性又具有参数简洁性,使得模型既能适用于不同的机制,又能使模型易于求解,降低模型的计算难度。根据参数取值的不同,权重函数可以表现出多种曲线形式。 根据模型可知,高频数据Xj在每个t-1到t区间内,都具有一段相同的权重函数值,即每一个高频数据的权重函数都表现为周期是mj的周期函数。任何常用的周期函数都可以用傅里叶级数展开的形式来表示,因此权重函数fi(x)可以设置为傅里叶级数的形式,根据实际数据的特征,调整傅里叶级数中参数的设置,可以呈现出不同的函数形态。权重函数的具体形式为: 其中: 若已知系统行为因素与混频相关因素之间关系的分布函数,则求出分布函数在各点的取值,将分布函数作为权重函数的初始值;若缺乏系统白化信息和高频数据的分布信息,则将等值函数作为权重函数的初始值,构造优化模型,通过优化算法获得高频数据的权重函数中参数的估计值,求出权重函数。 对于实际给定的某一系统,系统行为序列与相关因素序列之间往往存在某种非线性关系,在建模过程中,必须事先给定权重函数的具体形式,进而建立模型,求得系统行为因素的时间响应式。但并非所有系统都能明确给出混频变量之间权重函数的具体形式,本文从建模精度的角度考虑,在平均相对误差最小化的目标下,建立以下非线性优化模型,通过模拟退火算法进行参数寻优。 在平均相对误差最小化目标下,按照如下步骤,可完成权重函数的寻优和相应的最小二乘求解。 第1步初始化:设置初始温度T0、初始解状态X0、每个T值的迭代次数L; 第2步对每个k=1、2、…、L,执行第3—6步; 第3步产生新解X′; 第4步计算增量ΔE=E(X′)-E(X),其中E(X)为评价函数; 第5步若ΔE<0,则接受X′作为新的当前解,否则以概率exp(-ΔE/T)接受X′作为新的当前解; 第6步若不满足终止条件,使得T逐渐减小,且T→0,然后转第2步;如果满足终止条件,则结束程序,输出结果。 综上,MFGM(1,N)模型的建模及预测可以分为如下几步: 步骤1模型变量的选取。根据实际案例,分析系统变量及包含与系统变量同频和混频的相关因素变量,根据定义4构建MFGM(1,N)模型; 步骤2构造权重函数。若已知系统行为信息及混频相关因素变量中高频数据的分布信息,则求出分布函数在各点的取值,将分布函数作为权重函数的初始值;若缺乏系统白化信息和高频数据的分布信息,则将等值函数作为权重函数的初始值,代入MFGM(1,N)模型中,并估计模型参数; 步骤3构造优化模型。通过模拟退火算法获得高频数据的权重函数中参数的估计值,求出权重函数后,代入MFGM(1,N)模型中,并估计模型参数; 步骤4依据定理2计算系统行为序列的时间响应函数,并进行模拟和预测分析,检验模型精度;若模型误差超出容忍范围,则转回步骤1,重新对相关因素变量进行分析; 步骤5采用MFGM(1,N)模型预测主系统行为序列,并对预测结果的合理性和有效性进行分析。 干旱灾害使粮食产量的波动幅度增大,特别是遭遇持续多年的严重干旱,干旱灾害造成粮食减产对粮食供应安全有一定的影响。因此,有必要对旱灾造成的粮食减产量进行分析,了解影响粮食减产的要素,以期尽量减少未来干旱对粮食产量的影响,进而保证我国粮食生产安全和降低生产成本。 各地历年的旱灾粮食减产量数据是分析干旱灾害造成的粮食减产状况的必要基础数据,因此,以平均减产分成法[21]对历年旱灾粮食减产量进行估算。该方法是农业部、民政部、统计局常用的计算方法。将减产10%以上、减产30%以上、减产80%以上的农作物播种面积,分别称为受灾面积、成灾面积、绝收面积。以历年旱灾受灾面积、成灾面积和绝收面积的统计数据为依据,推算旱灾粮食减产量,计算公式如下: W=[F3·D3+(F2-F3)·D2+(F1-F2)·D1]·A。 式中:F1为旱灾受灾面积,hm2;F2为旱灾成灾面积,hm2;F3为旱灾绝收面积,hm2;D1为减产1~3成,取平均数2.0;D2为减产3~8成,取平均数5.5;D3为减产8成以上,取平均数9.0;A为单位面积的粮食产量,kg/hm2。 选取2006—2017年安阳市因旱灾导致的粮食产量损失作为系统行为特征变量,降水量、温度及有效灌溉面积作为相关因素变量。其中,有效灌溉面积为年度数据,来源于河南省统计年鉴,时序图如图1(a)所示;降水量、温度数据为月度数据,来源于中国气象数据共享网,时序图如图1(b)、图1(c)所示。历年旱灾受灾面积占比、成灾面积占比和绝收面积占比如图1(d)所示。 基于安阳市因旱灾导致的粮食产量损失、降水量、温度及有效灌溉面积4个变量建立MFGM(1,4)模型,将粮食作物的水分敏感指数与温度敏感指数作为初始权重函数值,对安阳市因旱灾导致的粮食产量损失进行预测分析。 利用模拟退火算法,对模型中权重函数的参数值进行优化。模拟退火算法中参数设置如下:马尔科夫链长度为20,衰减参数为0.998,步长因子为0.001,初始温度为100,容差为0.01。由于2015年粮食产量损失极小,属于扰动数据,若参与建模会引起结果异常。因此,选用2006—2014年数据作为建模数据,通过优化算法得到最终的预测结果,模型拟合结果见表1。 选用2016—2017年数据作为样本外推预测,并计算预测精度。MFGM(1,4)的输出结果见表2。 图1 原始数据时序图 年份实际值/(万t)MFGM(1,4)模拟值/(万t)绝对误差/(万t)相对误差/%经典GM(1,4)模拟值/(万t)绝对误差/(万t)相对误差/%2006132.241 ———— — —2007131.760 114.479-17.281 -13.12 136.701 4.941 3.752008131.334 149.30017.966 13.68 148.249 16.915 12.882009205.685 207.2461.561 0.76 188.798 -16.887 -8.21201014.007 13.382-0.625 -4.46 19.726 5.719 40.832011136.910 141.8334.923 3.60 136.047 -0.863 -0.632012125.923 114.724-11.199 -8.89 130.368 4.445 3.532013128.360 141.87513.515 10.53 145.599 17.239 13.432014366.028 369.2603.232 0.88 336.160 -29.868 -8.16 表2 安阳市因旱灾导致的粮食产量损失实际值与MFGM(1,4)模型的预测结果 仅对实际值与模拟值进行比较,可能不足以体现“混频”的优越性。因此,采用低频的降水、温度数据,建立经典GM(1,4)模型。对比MFGM(1,4)与经典GM(1,4)两种模型的模拟精度,具体数据见表1。对于经典GM(1,4)模型,由2006—2014年的相对误差值可以计算得到平均模拟误差为10.623%, 误差小于15%,经典GM(1,4)模型的残差检验合格,但相对于MFGM(1,4)模型而言,经典GM(1,4)模型精度较低。 为了进一步说明MFGM(1,4)模型的合理性,对其预测结果进行残差检验与关联度检验。 将预测值与实际值相减再取绝对值得到绝对残差序列,再将得到的绝对残差值与相应的实际值相除得到残差序列。MFGM(1,4)模型对2006—2017年安阳市因旱灾导致的粮食产量损失预测的相对误差结果见表1和表2。由2006—2014年的相对误差值可以计算得到模拟值的平均相对误差为6.21%, 由2016—2017年的相对误差值可以计算得到预测值的平均相对误差为7.43%,所有误差均小于15%,所建立模型的模拟预测结果的残差检验合格,且模型的预测精度相对较高。 关联度表征两列数据之间的相似程度,关联度检验即检验原始数据与模拟数据曲线之间的相似程度。因此,选用该方法进一步验证实际值与模拟值之间的联系。 使用灰色关联度,将实际值作为原始序列,模拟值作为比较序列进行关联度检验。如果两序列的关联度γ满足γ>0.6,则模型的关联度检验合格。 计算可得,两序列之间的关联度为0.632,大于0.6,满足条件。因此,所建立的MFGM(1,4)模型模型关联度检验合格。 1)随着监测、统计手段的丰富和途径的多样化,在社会、经济、生态系统的分析中,具有混频特征的多元数据会越来越多。本文构建了系统特征数据为低频、相关因素数据为混频的MFGM(1,N)模型,并给出了参数优化方法,为解决具有混频数据特征的小样本系统建模问题提供了有效工具。 2)MFGM(1,N)模型的参数取值完全由数据自身驱动产生,在不同频次数据的处理上具有很强的客观性。MFGM(1,N)模型是经典GM(1,N)模型的拓展,当混频数据退化为同频数据且不存在滞后性时,MFGM(1,N)模型退化为经典GM(1,N)模型。 3)采用MFGM(1,4)模型来模拟因旱灾导致的粮食产量损失与降水量、气温和播种面积之间的响应关系。结果表明,本文提出的MFGM(1,N)模型对粮食产量损失的模拟和预测精度均高于经典GM(1,N)模型的。





1.3 高频权重函数设置
1.4 权重函数选择
1.5 建模步骤
2 实例分析
2.1 模型构建及预测结果分析


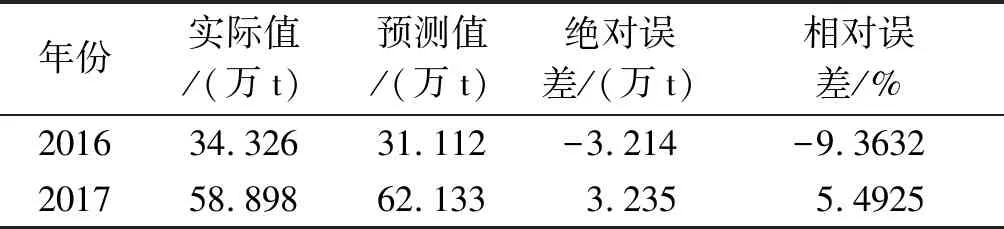
2.2 对比分析
2.3 残差检验
2.4 关联度检验
3 结语
