基于经纬仪的光束平差法定向方法改进

王伟瑶 尤智伟 黄 剑

(上海航天设备制造总厂有限公司，上海 200240)

1 引 言

经纬仪工业测量系统因其测角精度高、测试无接触、测量范围大、便携性好等特点，广泛应用于大尺寸空间三维点坐标测量、准直立方镜姿态测量等检测任务中。所谓系统定向，是指确定单台经纬仪与测量基准坐标系之间的空间六自由度位置关系，即沿坐标系三坐标轴方向的平移、旋转参数。精确互瞄法和光束平差法是两种经纬仪系统定向的主要方法。其中，基于前方交会原理的精确互瞄法大量运用于航天、航空、军工等领域中，基于透视投影原理的光束平差法由于照准精度要求高、解算需要迭代、解算存在危险角度等缺点，使用率不高。然而，随着工业技术的发展，产品的结构越来越复杂，在许多情况下，经纬仪测量系统需要在非通视条件下进行测试[1]。以通视条件为前提的精确互瞄法无法实现非通视条件下的系统定向。

图1所示为某航天器总装精度测试中的测站布局示意图，按设计要求需保证舱体内部设备与舱体外部设备之间的空间位置参数，舱内外多台测站间的互瞄光路被产品隔绝。本文所提及的非通视条件，均为图1所示的部分非通视条件，即仅隔绝互瞄光路。

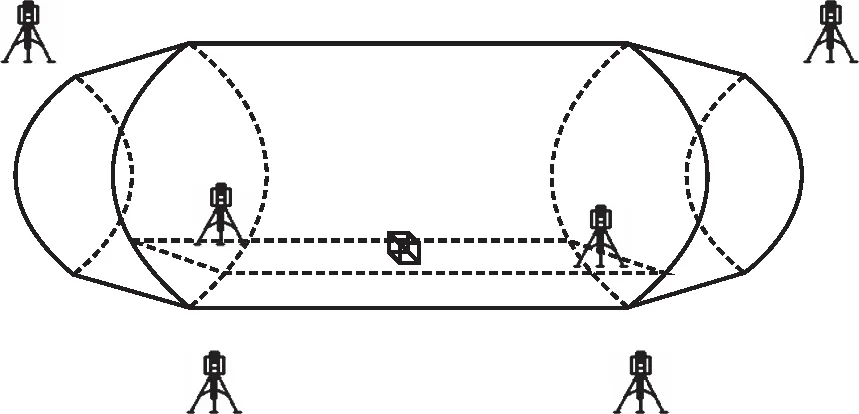
图1 航天器舱体精测布局图

光束平差法不需要测站之间精确互瞄，可选择具备公共视野的地点放置基准完成定向，可以适应图1的测试环境。在场地适应性上，脱离了互瞄光路的限制，较之精确互瞄法更加灵活。但是这种定向方法难以消除基准点的照准误差，每一个基准点的两个观测角误差都会累积影响解算，往往无法得到满足测试精度的定向结果。针对这种现状，笔者提出了一种结合两种定向模型的改进方法，在光束平差法的基础上加入经过互瞄并解算基线长度的两台测站作为基站，修正仪器照准基准公共点时的观测角误差，实现在系统内除基站以外所有仪器非通视的限制条件下，维持不低于精确互瞄法的测试精度，完成系统定向。

2 基础定向方法分析

2.1 光束平差法的简化

如图2所示，根据透视投影理论[2]，将经纬仪的水平角、竖直角观测值转换为虚拟像平面坐标。以经纬仪T1的垂直大地水平向下为+Y，T1的水平角零位方向为+X，通过右手定则拟合出+Z方向，得到一个测量坐标系O1-X1Y1Z1，同理可得T2的测站坐标系O2-X2Y2Z2。P点在测站坐标系下的点坐标如下:

图2 光束平差模型示意图

(1)

式中：x、y、z——分别P点的坐标值；H——两台测站的水平角读数；V——两台测站的竖直角读数；i=1,2。

如果提出一个限制条件，限定所有测站在精确整平后测试，测站2相对测站1的旋转关系只绕y轴旋转α°。该限制条件将极大地简化模型后续的计算，同时也符合大多数场所的测试工状，经纬仪的电子水泡与补偿器可以精确整平仪器。根据坐标系的旋转、平移关系，P点在左右测站坐标系下的坐标值存在如下对应关系：

(2)

式中：t1、t2、t3——测站1坐标系原点在测站2坐标系下的坐标值。将矩阵转换为等价的方程组：

(3)

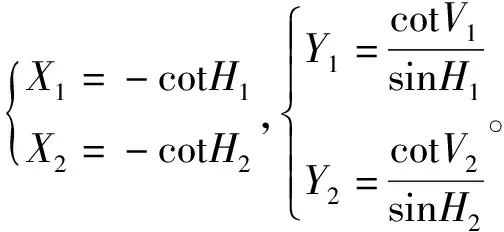
(t1-X2×t3)×[Y2×(-sinα×X1+cosα)-Y1]=

(t2-Y2×t3)×[X2×(-sinα×X1+cosα)-(cosα×X1+sinα)]

(4)

若将等式两边同除以t3[3]，并将旋转角的正弦值作为变量，余弦值按正负号分情况讨论，可进一步化简为如下形式(假设余弦值为正)：

(5)

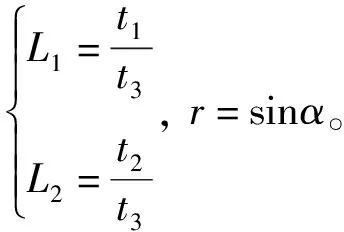
公式(5)包含了3个未知参数L1、L2、r，使用测站1与测站2瞄准1个空间点和一根长度为d的基准尺的两侧端点，可以得到3组类似式的对应关系，将这三组关系式联立成方程组，通过牛顿迭代法解算出旋转角r和平移比值L1、L2。根据基准尺长度d，以下式解算t3，从而得到两测站间的所有定向参数：

(6)

(7)

式中：X1、X2、Y1、Y2——分别为测站1与测站2观测空间点P时的角度读数相关三角函数，X11、X12、Y21、Y22——分别为两台测站观测基站尺两端点时的角度读数相关三角函数。

2.2 定向误差的实用性分析

通过三组测试数据，由公式(5)改写为以下关系式：

F=f1+f2+f3=0

(8)

式中：f1、f2、f3——分别对应一组观测值。代入公式(5)得到的多项式

将F以泰勒级数展开，假设观测角的测量误差在±3″区间内，可将观测角读数与迭代所得定向参数视为近似值，忽略二次项以上多项式，得到以下关系式：

(i=1,2,j=1,2,3)

(9)

从公式(9)可见，如果六项观测角多项式的任意一项存在误差，为了满足和为0的条件，都将使三项定向参数产生偏差，三个空间点的测量误差将累积影响定向参数。光束平差法直接将带有照准误差的测角读数作为方程组系数，方程组的解指向错误的定向位置。在该位置，测站视准轴以带有照准误差的测角读数在空间点P处完美交会。模型内缺少其他精度更高的参数构造约束条件来判断照准误差、定位误差。

3 改进方法

3.1 引入约束

为了解决这个问题，在多台仪器联机测试模型内添加两台已经精确互瞄并解算基线长度的经纬仪作为基站。在测试图1所示的舱体时，因为兼顾并行工序的要求以及现场场地的限制，为了满足测试舱体内部基准立方镜与舱外设备的相对位置关系的设计要求，在诸多限制下只得如图3所示布局仪器，组成测量坐标系。仅舱内的两台测站T1、T2具备互瞄条件，舱外其余测站所有的互瞄光路被隔绝。将T1、T2精确互瞄并选作基站，在具备公共视野的区域与基站同时测量基准尺两端与两个空间点位靶标，用光束平差法解算各测站相对T1、各测站相对T2的旋转、平移参数。该方法在完成初步定向的同时，两台基站T1、T2可对其余测站形成虚拟互瞄轴约束。

3.1.1虚拟互瞄轴约束

如图3所示，以修正T3的定向参数为例，当三个式(5)形成的方程组有解时，T1与T3的视准轴必定以指定角度的水平角、竖直角两两相交，且交点位于基准尺两端与空间点位靶标。根据三角形相似原理可证以T1、T3的连线上任意一点作为测站中心，以相同零位、水平、竖直角读数形成的视准轴都将与T1的视准轴相交。同理，T2与T3照准相同的基准点后也能指定一条相同的连线。当T1、T2照准基准点的观测角为真值时，T3的测站坐标必定位于T1-T3连线与T2-T3连线的交点处。这两条连线即T1、T2与T3互瞄时的互瞄视准轴线，在非通视条件下是无法测量到的，但可以通过光束平差法解算得到的平移参数比值确定，因此将这两根轴线称之为虚拟互瞄轴。该条件是T1、T2两台仪器同时对T3形成的，约束了T3相对基准的旋转与平移参数比例，即T3初始零位固定，且测站中心位置与虚拟互瞄轴交点重合。

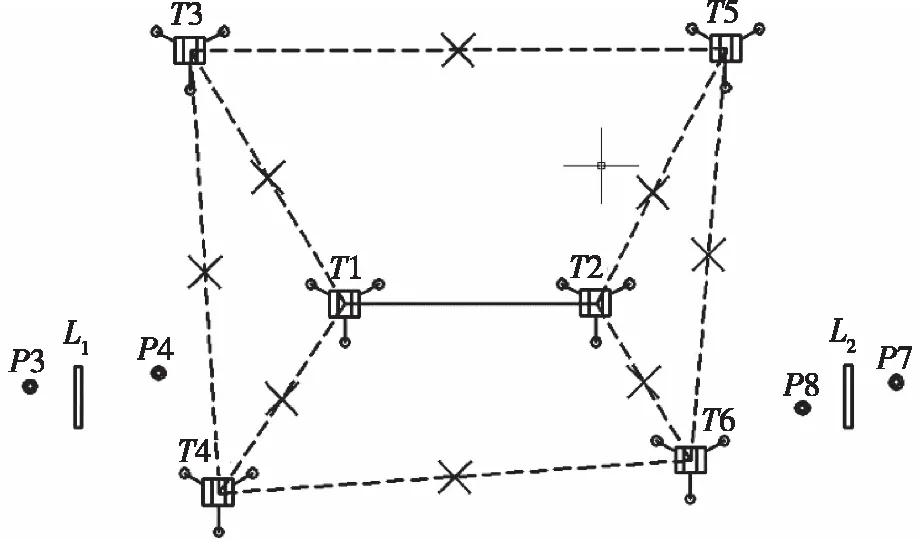
图3 测站定向投影示意图

3.1.2基线长度约束

同时基线长度对T3的测站位置形成另一个约束。如图4所示，在虚拟互瞄轴上，T3存在唯一位置满足照准轴交点间的点距与基准尺长度d相等。该条件建立了T1或T2单台仪器与T3的空间关系，约束了T3与该仪器之间的基线长度，确定了T3在虚拟互瞄轴上的具体位置。

3.1.3定位精度判定条件

通过牛顿迭代法分别解算T1与T3、T2与T3的光束平差方程组，可以得到两组满足基线长度约束的T3测站坐标。如果T3不存在照准误差，则这两组T3测站坐标与虚拟互瞄轴交点必定三点重合。然而，考虑到照准误差的累积，部分交会角不理想，满足三点重合条件的测站位置并不唯一。为了剔除粗差、方便后续平差，因此T3与T1、T2还需观测第四个基准点，以此验证在满足三点重合条件的测站位置上，以规定角度形成的视准轴能否与T1、T2的视准轴在第四点交会，确保测站位置的唯一性。所以，三点重合条件与第四点交会条件可当作解算、编程时的判定条件，来判断光束平差法的定位精度是否符合要求。

图4 视准轴相交示意图

3.2 约束条件的计算

3.2.1 虚拟互瞄轴的单位向量

如上文虚拟互瞄轴约束介绍，虽然基站T1、T2与T3无法互瞄，但仍能解算出T1、T2指向T3时的单位矢量。以T1为例，根据公式(4)，建立T1与T3的定向关系，两边同除以t2：

(10)

以三组空间点位的观测数代入式(10)中，以牛顿迭代法求解，可得到T3相对T1的平移参数对t2方向分量的比值M1、M3。同理，由式(5)的解算结果，可得到T3相对T1的平移参数对t3分量的比值L1、L2。按符号象限分别计算T1指向T3时的水平角θ和竖直角ε：

(11)

(12)

根据水平角θ与竖直角ε，同时通过建立基准时的互瞄值已知该测站零位相对基线的旋转角φ，可得T1的旋转矩阵：

(13)

矩阵R第一列元素是X轴的三个分量，即为虚拟互瞄轴的单位矢量：

(14)

3.2.2两虚拟互瞄轴的最短距离中点

假设T1虚拟轴矢量为μ，T2虚拟轴矢量为γ。T1测站坐标指向T2测站坐标的矢量为ω。当两虚拟轴在T1-T2测量坐标系下取到最短距离时，各自直线上的最近点坐标对应向量为：

(15)

两点距离为最大不相交误差，它们的中点为虚拟互瞄轴的相交坐标，下文简称虚拟相交坐标。

3.3 照准误差的修正

比较虚拟相交坐标与光束平差方程解算坐标，若虚拟相交坐标与解算坐标重合，且T3与T1、T2在基准点P4上的交会，则说明T3的照准误差符合精度要求；反之，若以上两个条件有其中之一没有达成，则说明定位误差过大，照准基准点的水平角、竖直角读数需要修正。

假设T3的照准精度存在±2″的误差，将这组照准读数视为近似值。笔者在本文提出以1″为精度遍历T3的6个观测角读数在±2″区间内所有数值，对每一个数值都进行三点重合与第四点交会判定，循环执行直到找到一组符号定向精度的照准读数，使之对应的解算结果同时满足上文提到的约束条件。该方法计算量大，迭代次数多且耗时。但是判断条件明确，如果测量误差在规定的区间内，必定可以得到高精度的定向数据。通过编程可以大量节省运行时间，预设的遍历区间越大，运行时间越久。使用clock函数计算执行一次迭代所消耗的时间为0.025s。遍历±2″的所有值，理论上每层循环需要遍历-2″至+2″的5个浮点型数字，6层循环需要执行15625次迭代，运行时间为390.625s。

3.4 基准最大不相交误差分配

上文所示的约束计算方法中，T1、T2的测点角度读数都是作为方程组系数加入解算，如公式(9)分析，是影响解算精度的误差来源之一，需要较高的测量精度。然而点位的测试精度依靠测试人员的人眼保证，可靠性有待验证。为了提高观测质量，不仅需要作多余观测，同时也需要将最大不相交误差平均分配给两台基站，以消除两台基站点位不交会的矛盾。如图5所示，假设T1、T2的以满足最大不相交误差的前提下测量基准点，得到符合两根视准轴最短不相交距离的中点坐标。分别连接T1、中点与T2、中点，得到的两根新的照准轴对应的观测角即为修正后的值。

图5 视准轴交会误差示意图

4 试验数据

为了验证上文方法的实用性，本文将通过一组定向实验，以精确互瞄法作为参照，对比新方法修正后的定向效果。将六台经纬仪以及基准尺、基准点按图3所示方位布置，模拟图1所示的舱体测量环境。先使用精确互瞄法标定测站，通过测试软件MetroIn[4]得到的观测值和解算结果如表1所示。

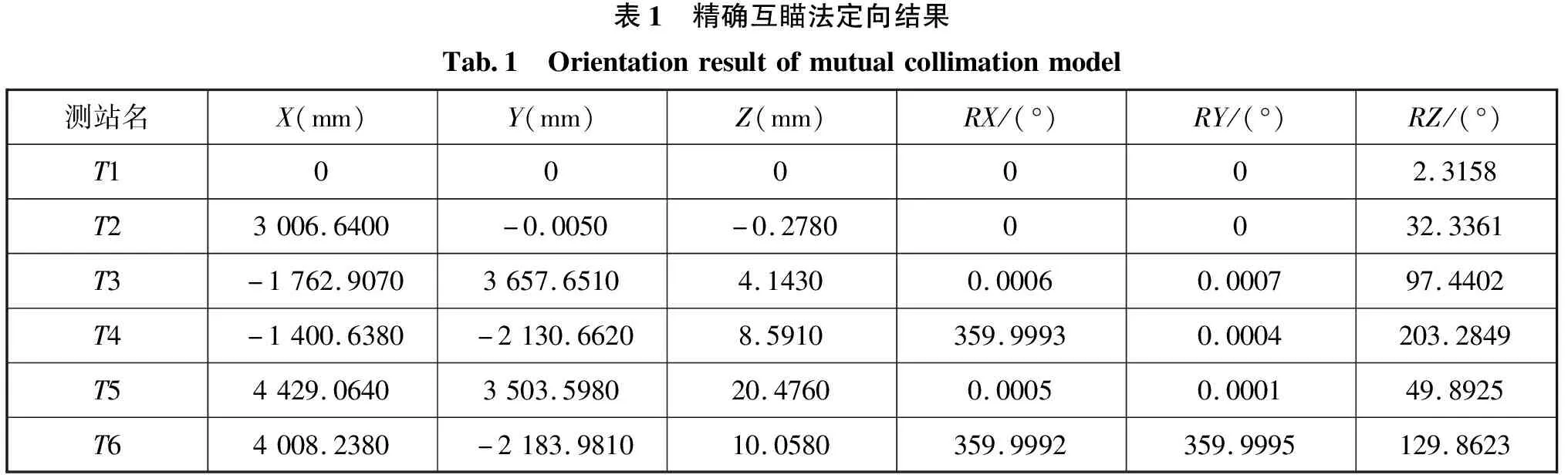
表1 精确互瞄法定向结果Tab.1 Orientationresultofmutualcollimationmodel测站名X(mm)Y(mm)Z(mm)RX/(°)RY/(°)RZ/(°)T1000002.3158T23006.6400-0.0050-0.27800032.3361T3-1762.90703657.65104.14300.00060.000797.4402T4-1400.6380-2130.66208.5910359.99930.0004203.2849T54429.06403503.598020.47600.00050.000149.8925T64008.2380-2183.981010.0580359.9992359.9995129.8623

以1～2测量坐标系为基准，假设除T1、T2以外其他测站皆无法互瞄，且只能观测到相应单侧基准。表2为牛顿迭代法解算得到的测站关系转换到1～2测量坐标系下的结果，每台仪器都存在±3″的照准误差。

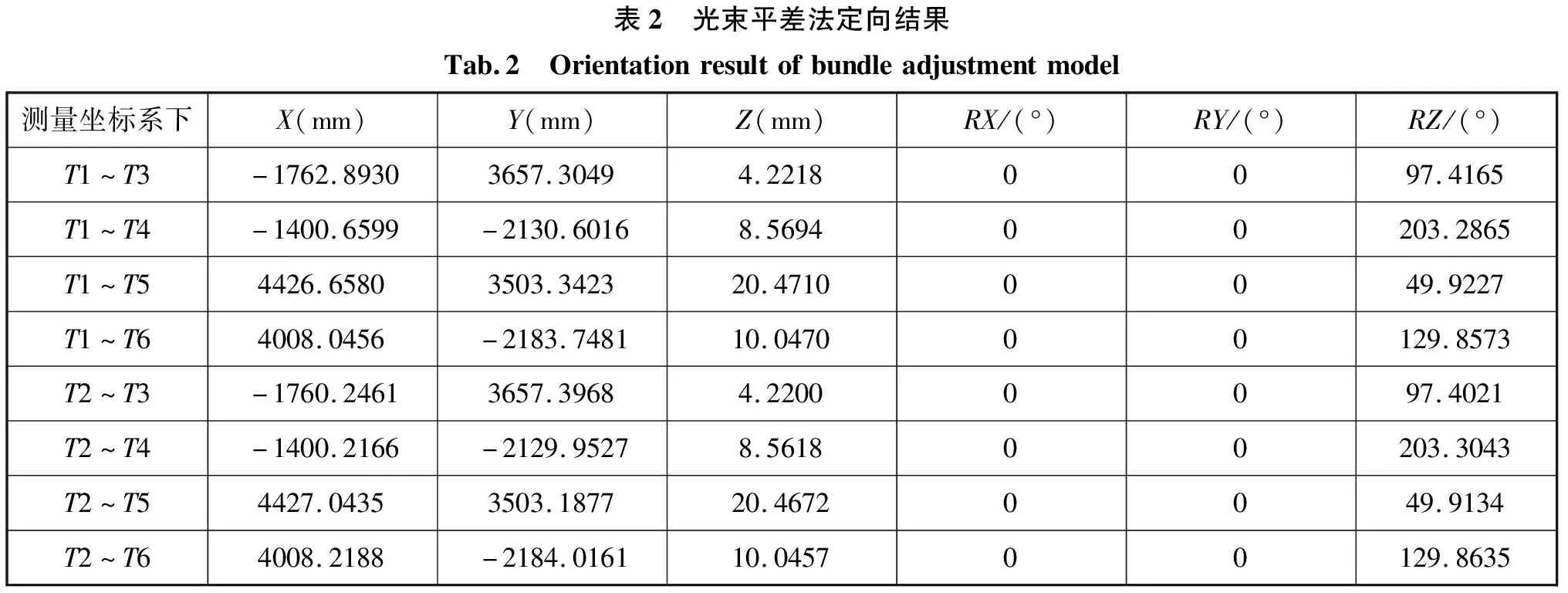
表2 光束平差法定向结果Tab.2 Orientationresultofbundleadjustmentmodel测量坐标系下X(mm)Y(mm)Z(mm)RX/(°)RY/(°)RZ/(°)T1^T3-1762.89303657.30494.22180097.4165T1^T4-1400.6599-2130.60168.569400203.2865T1^T54426.65803503.342320.47100049.9227T1^T64008.0456-2183.748110.047000129.8573T2^T3-1760.24613657.39684.22000097.4021T2^T4-1400.2166-2129.95278.561800203.3043T2^T54427.04353503.187720.46720049.9134T2^T64008.2188-2184.016110.045700129.8635

计算约束条件，T1、T2指向其它测站的虚拟互瞄轴相交坐标表3所示：

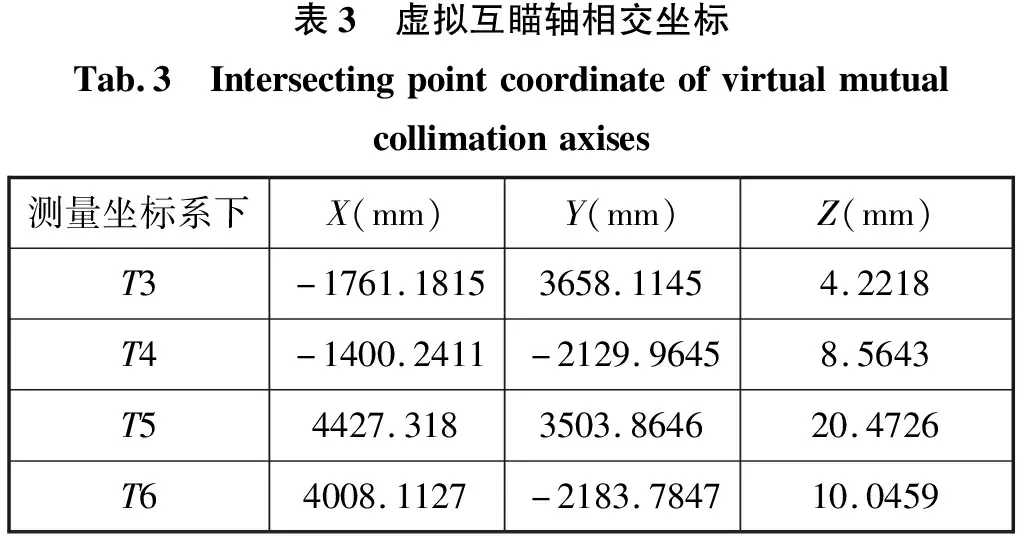
表3 虚拟互瞄轴相交坐标Tab.3 Intersectingpointcoordinateofvirtualmutualcollimationaxises测量坐标系下X(mm)Y(mm)Z(mm)T3-1761.18153658.11454.2218T4-1400.2411-2129.96458.5643T54427.3183503.864620.4726T64008.1127-2183.784710.0459

从数据判断，迭代所得的测站坐标与虚拟互瞄轴相交坐标不重合，并且与精确互瞄法的定位参数对比，发现存在毫米级的定位偏差。对测量结果进行修正，修正后的定向参数如表4所示：

两种定向方法的效果对比如表5、表6所示。

试验数据表明，光束平差法在未修正前，3″的照准误差将使测站零位角度偏离2′，测站坐标偏离2mm以上。修正后的角度精度可控制在10″以内，测站坐标精度约为0.1mm。

5 结束语

本文在经纬仪光束平差法的基础上，对解算模型加以简化，以两台已经定向完成的测站作为新的基准，建立了新的约束条件，修正了其余测站定向阶段基准点照准的累积误差，有效提升了定向精度。然而改进后的光束平差法解算效率低、照准精度要求高的缺点依然存在，对于基准点观测角误差与定位误差之间的函数关系有待进一步的研究总结，以生成新的算法代替遍历法更高效地修正误差。

表4 修正结果Tab.4 Modifiedorientationresultofbundleadjustmentmodel点距坐标X(mm)Y(mm)Z(mm)RX/(°)RY/(°)RZ/(°)1^3-1762.90763657.64944.14260097.43962^3-1762.90753657.65024.14280097.43981^4-1400.6171-2130.63268.579400203.28572^4-1400.6189-2130.63358.579100203.28561^54428.99733503.440620.45300049.89362^54428.99833503.442420.45320049.89361^64008.2738-2183.927710.048100129.86032^64008.2734-2183.930710.048700129.8604

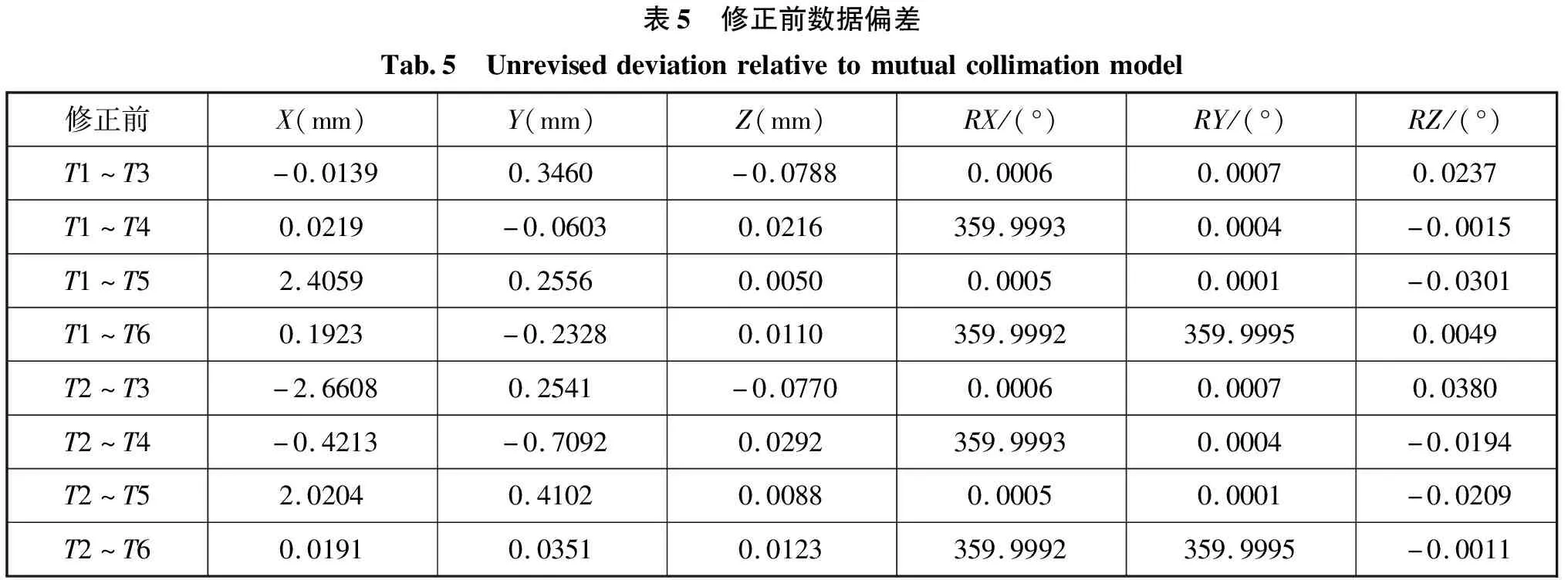
表5 修正前数据偏差Tab.5 Unreviseddeviationrelativetomutualcollimationmodel修正前X(mm)Y(mm)Z(mm)RX/(°)RY/(°)RZ/(°)T1^T3-0.01390.3460-0.07880.00060.00070.0237T1^T40.0219-0.06030.0216359.99930.0004-0.0015T1^T52.40590.25560.00500.00050.0001-0.0301T1^T60.1923-0.23280.0110359.9992359.99950.0049T2^T3-2.66080.2541-0.07700.00060.00070.0380T2^T4-0.4213-0.70920.0292359.99930.0004-0.0194T2^T52.02040.41020.00880.00050.0001-0.0209T2^T60.01910.03510.0123359.9992359.9995-0.0011

表6 修正后数据偏差Tab.6 Modifieddeviationrelativetomutualcollimationmodel修正后X(mm)Y(mm)Z(mm)RX/(°)RY/(°)RZ/(°)T1^T30.00060.00150.00030.00060.00070.0005T1^T4-0.0208-0.02930.0115359.99930.0004-0.0007T1^T50.06660.15730.02290.00050.0001-0.0011T1^T6-0.0358-0.05320.0098359.9992359.99950.0019T2^T30.00050.00070.00010.00060.00070.0004T2^T4-0.0190-0.02840.0118359.99930.0004-0.0007T2^T50.06560.15550.02270.00050.0001-0.0011T2^T6-0.0355-0.05020.0092359.9992359.99950.0018