纳米结构下激光波长对谐波截止能量的影响
2020-07-13王佳乐栗博文冯立强
王佳乐,栗博文,刘 航,冯立强
(1.辽宁工业大学 化学与环境工程学院,辽宁 锦州 121001;2.辽宁工业大学 理学院,辽宁 锦州 121001)
经过30年的研究,激光脉宽已经从皮秒量级发展到了飞秒和阿秒量级。当这种超短、超强激光场与物质相互作用时会产生许多有趣的非线性光学现象,例如阈上电离、双电离以及高次谐波[1-2]。这些现象成为探测原子、分子、等离子体和固体中的超快现象的有效工具。
高次谐波作为其中的佼佼者,更是被广泛研究。目前,激光驱动原子、分子辐射高次谐波的现象可以通过电离-加速-回碰三步模型来解释[3]。基于三步模型,谐波截止能量与激光强度呈正比同时与激光波长的平方也呈正比。因此,基于此条规则研究人员提出了非常多种行之有效的方案来延伸谐波截止能量,例如调频激光场方案[4]和叠加组合场方案[5-6]。
虽然谐波截止能量随波长的变化可以由三步模型来很好地解释,但是只局限在均匀激光场情况下,即激光场不考虑空间的变化。最近10年,纳米结构下所形成的空间非均匀激光场受到了很多关注。因为当激光场处于特定的纳米结构下时,激光场在该空间范围内会形成明显的空间变化。因此,此时必须考虑空间变化对激光场的影响。基于此,研究人员发现在空间非均匀场下,谐波截止能量会得到延伸[7-8]。但是,在空间非均匀场下,谐波截止能量对激光波长的变化规律却很少有人报道。
因此,本文研究了3 种非均匀激光场下谐波截止能量随激光波长的变化规律。
1 理论方法
本文研究体系为单个He 原子,其与激光场作用的薛定谔方程为[9](这里只给出主要公式,具体求解过程参考文献[9]):
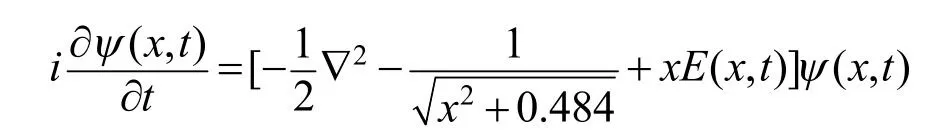
式中:x、t和Ψ为电子坐标、时间和波函数;为非均匀激光场,其中E、ω和β分别为激光场振幅、频率和非均匀参数。激光波包f(t)选为高斯波包。方程求解方法为二阶分裂算符方法[9]。本文纳米结构的宽度为550 a.u.,即本文电子运动范围在550 a.u.之内。
2 结果与讨论
图1 给出3 种不同非均匀激光场下He 原子谐波截止能量随波长的变化规律。激光强度为300 TW。激光波长变化范围在800~2 000 nm。激光全宽为各自波长的5 个周期的时间。由图可知,当β=0时,即采用均匀激光场时,谐波截止能量与波长平方呈正比,即Ecutoff∝λ2。这一结果与三步模型的预测是一致的[3]。随着非均匀参数增大,谐波截止能量得到延伸。具体来说,当β=0.001 时,谐波截止能量大致与波长的3 次方呈正比,即Ecutoff∝λ3.2。当β=0.002 时,谐波截止能量大致与波长的4 次方呈正比,即Ecutoff∝λ4.5。可见,谐波截止能量与波长成指数倍关系增大;并且随着非均匀参数增大,这种关系越来越大。这种现象非常有利于获得高能量的谐波平台区。

图1 不同非均匀场下谐波截止能量随波长的变化
但是,这里需要注意,当β=0.002 时,随着波长的持续增大(当λ>1 800 nm),谐波截止能量似乎达到了一个极限值,其值大致在1 800 eV。如果采用β=0.003 的非均匀激光场,依然可以观测到这个极限值的存在,但是发生的波长会提前,即λ>1 600 nm 时,这个极限值就会出现。为了解释这一现象,图2 给出了电离电子在纳米结构下的运动示意图。首先,由三步模型可知,电子在激光驱动下的最大运动距离为xmax=E′/ω2,其中E′是激光场在纳米结构下增强后的场强。其可由公式获得[10],其中Ip是He 原子电离能。利用上述2 个公式可以求得当β=0.002,λ=1 800 nm 时,电离电子需要的最大距离为572 a.u.。但是本文中电子的最大运动范围只由550 a.u.。也就是说,当电子的运动距离小于550 a.u.时,其可以返回母核并辐射谐波,如图2 上半部分所示。但是,当电子运动范围超过550 a.u.时,其被纳米结构吸收不能返回母核,即能量高于1 800 eV 的电子都被纳米结构吸收了,如图2 下半区域所示。因此,就会产生能量范围在1 800 eV 的阈值区域。
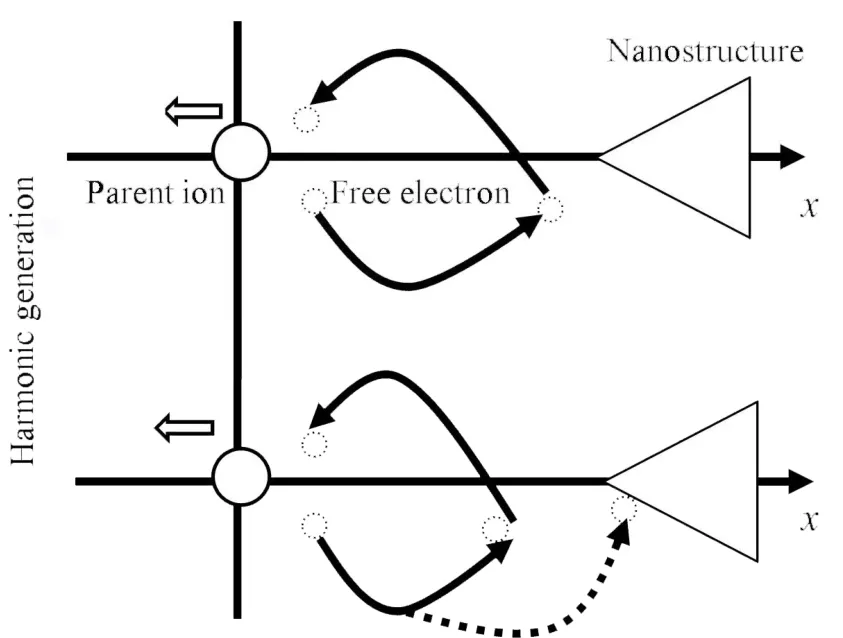
图2 电离电子在纳米结构下的运动规律
3 结论
理论研究了3 种非均匀激光场下谐波截止能量随激光波长的变化规律。结果表明,谐波截止能量与波长呈指数倍关系增大。随着非均匀参数增大,谐波截止能量延伸更为明显。但是,在每个纳米结构下,谐波截止能量存在一个固有的阈值。本文的研究成果为实验研究和后续理论研究提供了宝贵的参考数据。
