基于模糊层次分析法的非金属矿山安全生产风险研究
2020-07-13白世虎
白世虎
(宜昌市夷陵区应急管理局,湖北宜昌 443000)
湖北省磷矿资源丰富,储量高居全国第一,其中尤以鄂西宜昌地区为主,储量占全省储量的70%以上,遍布有71家磷矿企业。然而随着矿产资源的不断开采,部分矿山的开采深度也逐年增加,开采环境愈加复杂,井下冒顶片帮等事故频发。为有效应对和预防事故的发生,文章在建立有效数学模型的基础上,选取三宁矿业挑水河磷矿的井下作业系统,对其安全性进行定量的分析,从而确定其安全性,为矿山今后的健康安全发展提供参考依据。
1 非金属矿山安全生产评价数学模型
模糊综合评价法是根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价[1,2]。其一般步骤如下。
1.1 确定指标评价体系
首先建立综合评价指标集U,即目标层:
U={UA,UB,UC,UD,UE,UF,UG}={通风系统、供排水系统、…、安全管理},再建立准则层:Ui=(Ui1,Ui2,……,Uij)。
1.2 构建权重向量
采用层次分析法构建好权重向量。目标层的权重 W=(WA,WB,WC,WD,WE,WF,WG),准则层的权重为 Wi=(Wi1,Wi2,Wi3,Wi4……Wij),在非金属矿山生产作业安全评价中,不同的指标具有不同的功能,对系统的安全度的贡献也不同。因此需要对各个指标进行赋权。本研究采用业内普遍使用且较为成熟的方法——层次分析法。
层次分析法确定权重具体方法如下[3,4]:
1.构造判断矩阵,建立表1所示的“1-9标度法,问卷采用标度法,对全部指标进行两两比较。

表1 层次分析法1-9标度法
2.确定权重,根据建立的判断矩阵,采用“和积法”确定权重。
1.3 构建评价矩阵
建立适合的隶属函数从而构建评价矩阵。
1.4 评价矩阵和权重的合成
采用适合的合成因子对其进行合成,并对结果向量进行解释。
1.5 模糊综合评价
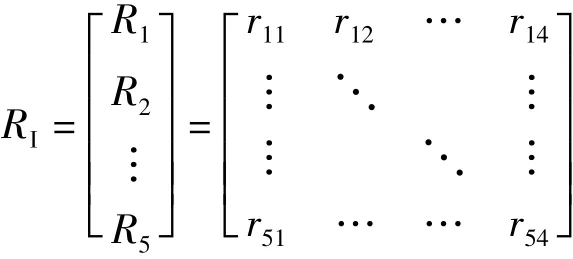
根据一级模糊综合评价结果,可以构成模糊关系矩阵R。将相应数据代入评价公式,可得:

2 以三宁挑水河磷矿构建非金属矿山安全评价指标体系
指标体系既是模型的核心,也是基础。评价严格遵守指标体系构建的科学性、系统性、可操作性,科学选择指标、选取和计算数据,计算数据通过调查问卷获取,本次调查问卷选取了46位长期从事矿山生产安全和技术的专业人员参加。
针对挑水河磷矿的现场作业环境,结合指标体系构建的原则,对作业单元进行了划分,建立了包括通风系统、供排水系统、供电与通信系统、爆破系统、运输提升系统、采矿系统和安全管理制度七个板块的评价指标体系[5,6]。
3 层次分析法确定挑水河磷矿安全评价指标权重
根据各指标的重要性的对比,通过matlab计算各指标权重,从而得到目标层的判断矩阵,见表 2[7,8]。
在层次分析法中,CR为判断矩阵的随机一致性比例,一般认为当CR<0.10时,判断矩阵具有令人满意的一致性,而所得到的结果就是目标层的判断矩阵。
根据所建立的判断矩阵,求得其特征向量为W=[0.165 4,0.224 0,0.183 0,0.099 3,0.137 3,0.089 7,0.101 2]T,最大特征根为 λmax=7.189 4,CR为0.023 2。经检验判断矩阵具有满意的一致性。目标层的权重值分别为 0.165 4,0.224 0,0.183 0,0.099 3,0.137 3,0.089 7,0.101 2。

表2 一级指标(目标层)判断矩阵
在得出一级指标判断矩阵后,运用相同方法可求得因子层的权重,分别对其它指标层进行计算,得到:
WA=[0.417 3,0.244 2,0.123 8,0.131 6,0.083 1]
WB=[0.227 8,0.210 3,0.157 0,0.191 5,0.137 7,0.075 8]
WC=[0.247 1,0.263 4,0.172 4,0.143 0,0.104 1,0.069 9]
WD=[0.273 0,0.306 4,0.174 1,0.140 2,0.106 3]
WE=[0.242 1,0.121 1,0.196 2,0.147 9,0.105 3,0.097 4,0.090 1]
WF=[0.493 4,0.310 8,0.195 8]
WF1=[0.285 7,0.285 7,0.285 7,0.142 9]
WF2=[0.249 8,0.189 0,0.253 5,0.207 9,0.099 9]
WF3=[0.325 7,0.356 4,0.193 6,0.124 3]
WG=[0.215 7,0.290 8,0.219 7,0.166 0,0.107 8]
CRA=0.042 1、CRB=0.053 2、CRC=0.049 2、CRD=0.045 4、CRE=0.032 0、CRF=0.051 6、CRF1=0、CRF2=0.045 4、CRF3=0.035 7、CRG=0.030 4,均具有令人满意的一致性。
由以上各判断矩阵得到指标体系及其权重。详见表3。

表3 指标体系及其权重
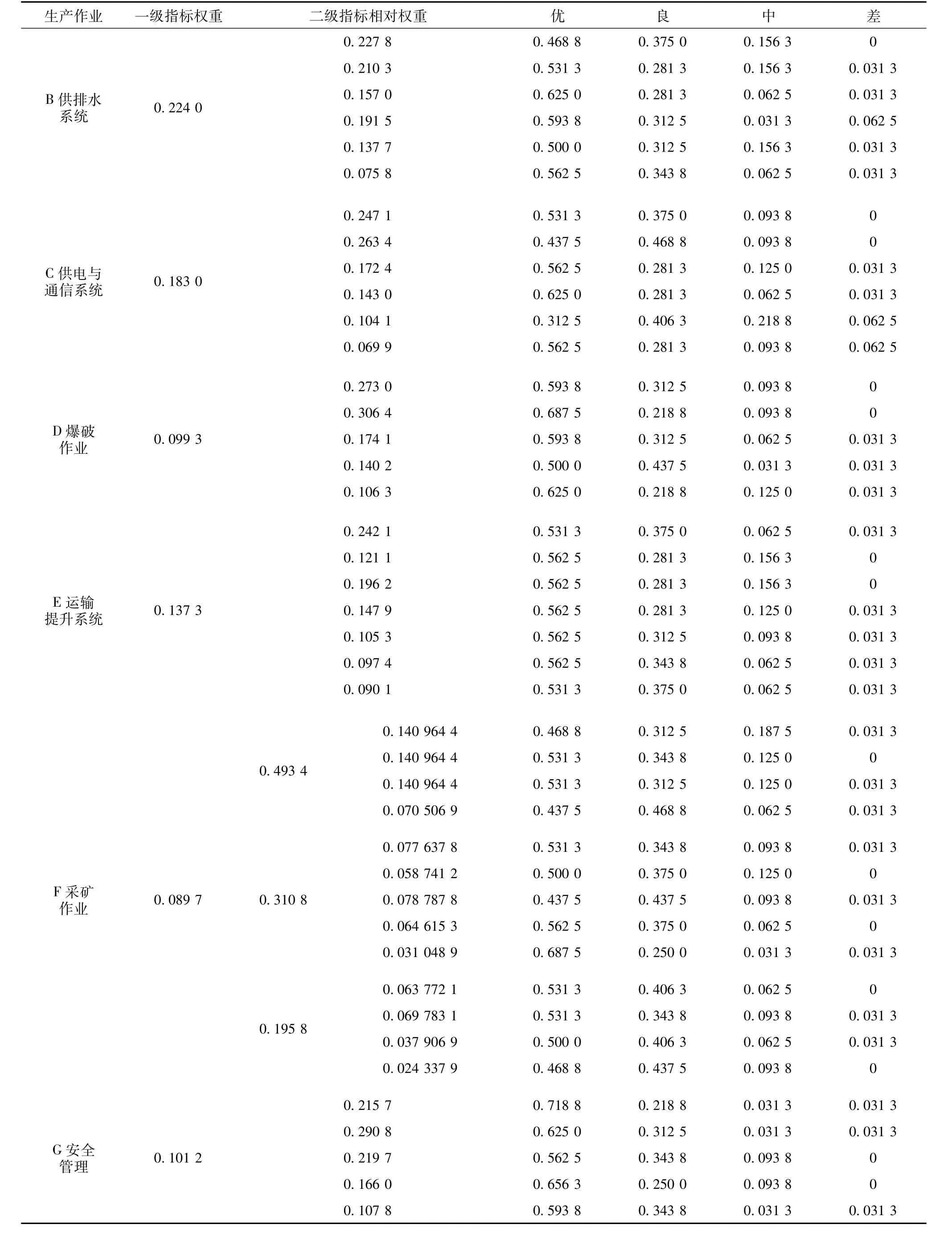
(续表3)
4 对目标层进行模糊综合评价
按照确定的底层评价指标的权重,可以组成各子系统的权重 A、B、C、D、E、F、G,则各系统的一级模糊综合评价结果,具体数值见表4。

表4 R隶属度情况
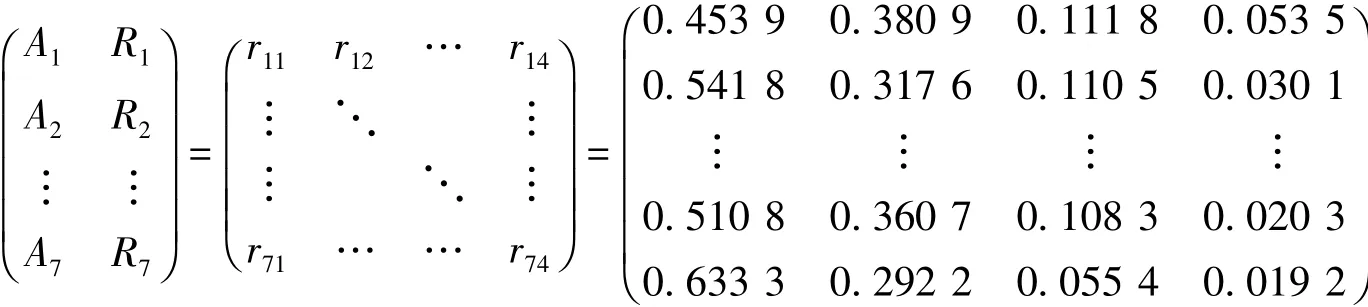
得到每一个准则层的模糊隶属关系后,计算准测层安全得分。计算方法为:
首先计算各模糊矩阵相对于准则层内的评语集得分:

其中,i=1~7;j为每个准则层内措施层的个数,在A1、A2、……、A7中的个数分别为[5,6,……,5];aij为第i个准则层内的第j个指标所占的权重,得到各准则层的评价得分为(详见表5):

表5 准则层评价得分
根据一级模糊综合评价结果,可以构成模糊关系矩阵R。将相应数据代入评价公式,可得:
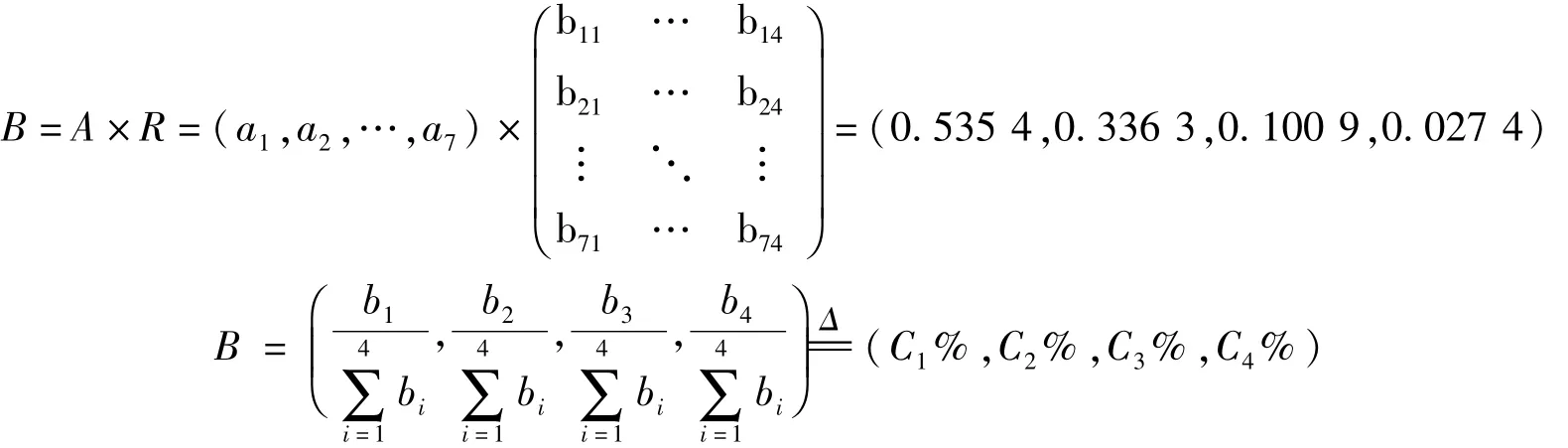
解得 C1=53.54,C2=33.63,C3=10.09,C4=2.74。
结果说明:对于评价对象风险评价等级,相关领域专家C1%的人认为可得4分,有C2%的人认为可得3分,有C3%的人认为可得2分,有C4%的人认为可得1分,进一步的,把4分、3分、2分、1分,作为4个档次。令 Y=(4,3,2,1)T,所以综合评价得分为:Z=BY,得到Z=4×C1%+3×C2%+2×C3%+1×C4%=3.379 66,可知安全性处于良好以上水平。表明该非金属矿山地下开采的安全性较好,但也需要采取进一步的防范措施,尤其是在通风系统和采矿作业环节,要采取必要的隐患排查治理措施,避免隐患事故的发生。
5 结 论
1.在分析非金属矿山地下开采安全风险因素的基础上,构建了项目安全评价指标体系,运用模糊层次分析方法,较为客观地反映该矿山地下开采安全状况。
2.通过问卷调查的方式对影响因素重要性进行比对,采取层次分析法对比对结果进行计算从而确定了各指标权重,增强了权重的可信度,从而提高了安全评价的科学性与可靠性。
3.根据该矿山地下开采模糊综合安全评价的结果,为对其它类似矿山的安全管理提供了参考,同时可以指导今后非金属矿山安全评价管理工作的顺利开展。
