对不同形状电热管加热效果的数值模拟研究

刘 凯 龙

(河北建筑工程学院，河北 张家口 075000)

0 引 言

目前，电力供热在我国具有广阔的发展前景，使得电锅炉蓄热系统发展迅速.根据锅炉和蓄热罐的相对位置，蓄热系统通常有二种型式：整体式和分体式.在整体式蓄热系统中，由于电热管往往集中在罐体的一端，造成加热不均匀，限制了整体式蓄热系统的应用.本文结合圆形度的概念，利用数值模拟方法探讨不同形状加热管在整体式电锅炉中的加热效果.其中，圆形度是图像处理中相当重要的概念，用于特征的提取和描述，定义为4π倍的区域面积A与周长P的平方之比，即C=4πA/P2.

随着计算机技术的发展，数值模拟可以达到对工程问题研究的目的.例如南京理工大学动力工程学院的张敏就曾对管状电加热器升温特性进行了数值计算，取得良好的结果，且相关数值模拟研究还有很多先例.本文采用GAMBIT建立简化的电热管模型，利用FLUENT求解计算不同形状的电热管在锅炉内的加热效果.电热锅炉结构及电热管形状见图0-1，电加热管纵截面为圆形，直径为10mm.电加热器的关键部分是加热管的结构设计及接线盒结构设计，在本文中，假设电加热器已经完成了结构设计和接线盒设计，且满足型式检验要求、图纸与技术要求[1].见图0-1三种形状的电热管均为双头电热管，用于加热部分长度均为2.05 m，三者的圆形度分别为1、0.7、0.4.

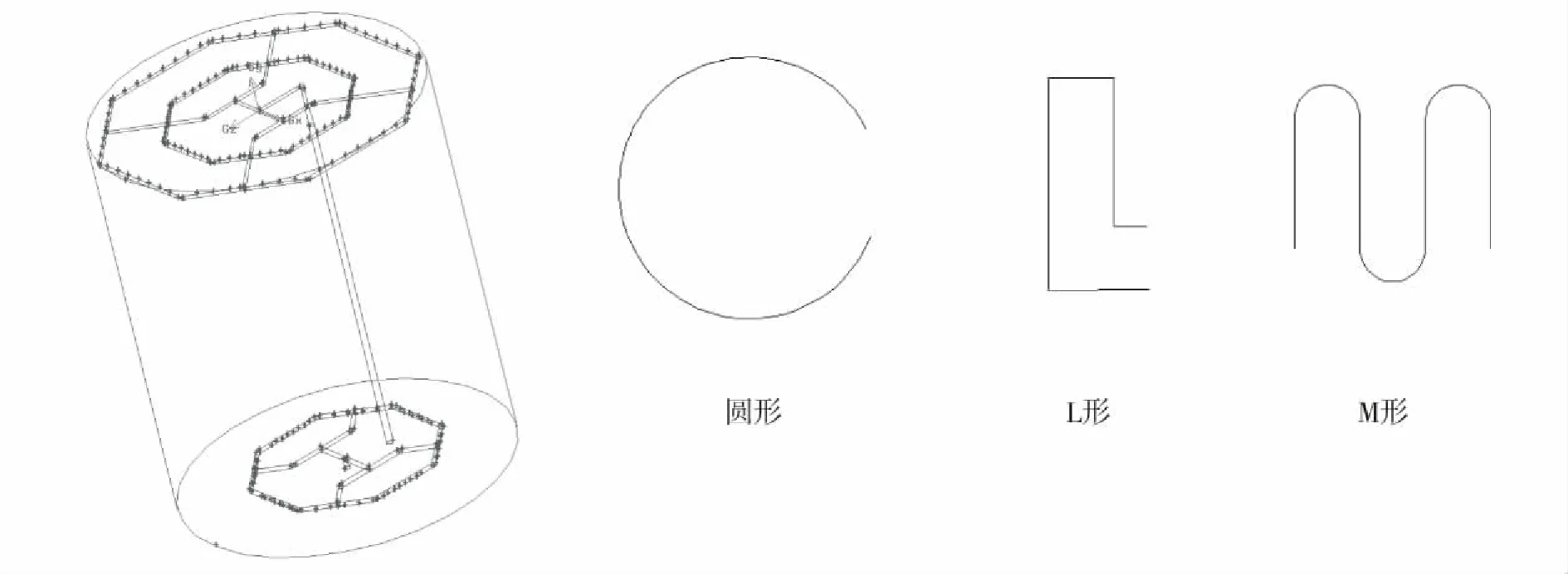
图0-1 模型简图

1 FLUENT计算过程

FLUENT数值计算过程可分为建立数学模型和数值计算两个过程，计算步骤：建立数学物理模型、确定离散方法、划分网格，生成节点、设置控制方程与模型、确定边界条件和初始条件、设置求解控制参数、求解离散方程、判断收敛与否、显示输出计算结果.

1.1 流体力学基本方程

流体力学控制方程有连续性方程、动量方程和能量方程，三者可以用通用形式表述为：

式中的φ值为通用量，可以代表u、v、w、T等求解变量；Γ为广义扩散系数；S为广义源项.u、v、w分别为x、y、z各方向的速度分量，m/s；ρ为密度，kg/m3.

1.2 一阶迎风离散

一阶迎风格式规定：因对流造成的界面上的φ值被认为等于上游节点(即迎风侧节点)的φ值.见图1-1，当流动沿着正方向，即ue>0，φe=φP.

图1-1 控制体积P及界面上的流速

定义F为通过界面上单位面积的对流质量通量，F=ρu.定义D表示界面的扩散传导性，D=Γ/δx.则一阶迎风格式的对流扩散方程的离散方程：aPφP=awφw+aEφE.

式中：aP=aE+aw+(Fe-Fw)、aw=Dw+max(Fw,0)、aE=De+max(0,-Fe)

1.3 SIMPLE数值计算方法

此算法是求解压力耦合方程的半隐式法.半隐是指将式中的压力修正对速度的间接或隐含的影响略去.SIMPLE算法的计算步骤为：

(1)假定一个速度分布，记为u0,v0,w0，以此计算动量离散方程中的系数和常数项；假定一个压力场p*.

(4)以改进的速度场求解aPPP=aEPE+aWPW+aSPS+aNPN+aBPB+aTPT+Sφ，如温度场、浓度场、紊流动能、紊流耗散等.

(5)利用改进后的速度场重新计算离散方程中的系数，并用改进后的压力场作为下一次迭代的初值，即把改进后的p作为一个新的压力p*，重复直至求得收敛解[2].

1.2 网格无关性验证

(1)问题描述.

不考虑流体(水)温度的一股流体以1.2 m/s的速度流入DN32管道，进入距水箱底部0.05 m的单圈八角型布水器(每段管段长度0.35 m，管径DN20，其上开孔数量8个，分两组，开孔分别朝向水箱底部和水箱角部)，流出后进入水箱(直径1.66 m，高度2.03 m)，流入距水箱顶部0.05 m的双圈八角型布水器(内圈布水器：每段管段长度0.35 m，管径DN15，其上开孔数量7个，外圈布水器：每段管段长度0.6 m，管径DN15，其上开孔数量7个，开孔朝向水箱顶部)，由此经DN32管道流出.

网格划分采用Tet/Hybrid类型，单元格式类型为TGrid.布水器网格节点步长参数定义为0.005，水箱网格节点步长参数定义为0.02.模拟验证加热面设为柱形水箱底面，74025.555 W/m2.计算机类型为M415-D187.

(2)输入并检查网格.

网格检查结果显示无网格体积为负数且检查完成无警告，可视为合格.

检验计算是否收敛：在整个迭代模拟计算过程中，当能量的残差值的收敛标准达到10-6时，并且其他所有变量的残差值的收敛标准达到10-3时，整个模拟计算过程才被认定为达到收敛[2].入口质量流量0.94759154 kg/s，出口质量流量-0.94759172 kg/s，由模型可知两者的流动方向相反，且其不平衡误差少于0.1%，可认为计算收敛.对比不同的水箱网格体积数3372702、3922064得出口温度363.98K、362.83K；对不同布水器网格体积数2043810、494618得出口温度363.98K、363.54K.上述结果误差不超过0.2%，故可认为网格划分合适.

2 模拟结果分析

2.1 横向截面温度云图

表2-1 不同圆形度的横向截面数据表

由温度云图2-1和表格2-1可知，当C取值为1时，观察温度云图，平面显现两种温度，其他温度云图显现一种温度.建立圆形度与努谢尔数的拟合关系式：相关系数R2数值为1，y=2257.5x2-2725.3x+2015.3，可见随着圆形度的降低，努谢尔数变小，换热效果减弱.以平面温度均匀性高为评价原则，L形状和M形状电热管较好.

C=1 C=0.7 C=0.4

2.2 竖向截面温度云图

C=0.7 C=0.4

根据表格2-2，对比电热管圆形度为0.7时的加热效果，竖向平均温度高于横向，对流换热效果竖向要高于横向.而电热管圆形度为0.4时，竖向平均温度要低于横向，但对流换热效果竖向高于横向.随着圆形度的降低，竖向温差变化较大，换热效果减弱.横向换热效果变化范围为6%，差值较小.

表2-2 横向和竖向截面数据表

2.3 不同功率换热效果分析

5kW 3kW

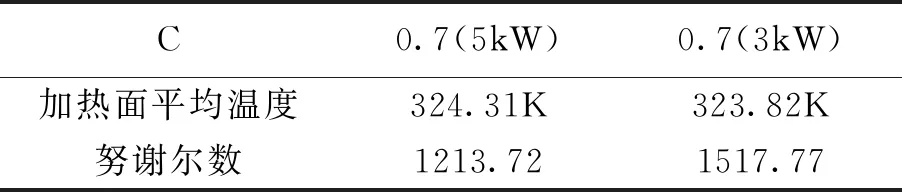
表2-3 不同电功率数据表

根据表2-3以圆形度0.7的电热管为例，对比电功率5kW和3kW的电热管，建立功率与努谢尔数拟合方程y=-152.03x+1973.8，相关系数数值R2为1，可见在一定范围内随着电功率减小，换热效果增强.类比同温冷热源的可逆循环，可知增强换热效果，应保证电力供应平稳.在相同尺寸下且满足生产要求时，应增大电功率.

2.4 多根电热管下数据

表2-4 不同管间距数据对比表

表2-4显示了3根圆形度0.7的电热管横向排列数据，建立管间距与努谢尔数拟合式y=241.4x2-1260.1x+3024.8，相关系数R2数值为0.941，可见随着电热管间距的减小，换热效果先减小在增强，转折点在间距为2.2倍的电热管管径处.对比流体出口温度，数值大小差值不超过1%，可见在加热过程中，电热锅炉出口温度可保持平稳.

表2-5 不同流速数据表

见表2-5，选用3根电热管，管间距为2.2倍的电热管管径，建立流速与努谢尔数拟合式y=0.1071x2+116.7x+786.79，相关系数R2数值为0.973，对比不同流速下的加热效果，随着流速减小，对流换热效果减弱，导热效果增强，电热锅炉流体出口温度随流速减小而增高.随着流速减小，电热管壁温增高，在蓄热电锅炉低谷时段采用边蓄边供模式时，故应合理考虑流速.

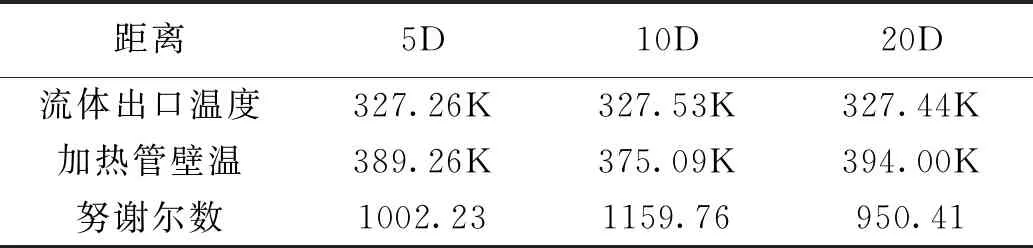
表2-6 不同距离数据表

见表2-6，采用3根电热管，管间距2.2倍的电热管管径，探讨电热管中心与上层布水器之间的距离对换热效果的影响.建立距离与努谢尔数的拟合式，相关系数R2数值为1，y=-3.4961x2+83.947x+669.9，随着距离增加，电热锅炉出口温度差值不超过1%，基本可认为保持不变.对流换热效果起伏不定，随距离增加先增加后减小，可见在电热锅炉中电热管的安装位置与电热锅炉常用的供热模式有关.

3 结 论

本文以常用的电热管形状为基础结合圆形度的概念，探讨了电热管形状和安装位置问题，得出圆形度0.7的L形电热管加热效果较好的结论.且存在多根电热管时，管间距应为2.2倍的电热管管径，流速和电热管的安装位置应结合电热锅炉的供热模式选择，达到增强换热效果的目的.本文不足之处一是由于相同的圆形度可具有不同的形状，未考虑相同圆形度不同形状的电热管换热效果.二是未考虑连续圆形度下的电热管换热效果.