Lorenz混沌系统的BLAKE哈希算法

王 娟， 周 鑫， 韩同壮

(黑龙江科技大学 电子与信息工程学院， 哈尔滨150022)

0 引 言

哈希函数是现代密码学中一类重要的基础密码算法，它将任意长度的数据输入经过变化得到固定长度的哈希值，在密码协议、数字签名、完整性认证等领域具有广泛应用。作为消息摘要函数标准SHA-3的第二轮候选算法，BLAKE哈希算法[1]运算速度快且安全性高。近年来，其相关密码攻击正被逐渐重视。Aumasson等[2]给出BLAKE-256压缩函数中间4轮的几乎碰撞攻击。Biryukov等[3]对BLAKE的7轮压缩函数和8轮置换函数进行了攻击，Dunkelman等[4]给出了BLAKE置换函数中间6轮的差分区分器。上述攻击表明，BLAKE哈希算法仍存在一定的安全隐患。

混沌系统的运动特征表现为对初始状态极度敏感性、确定的随机性、混沌序列的遍历性，这些特性恰好满足哈希函数中压缩函数的单向性、初值敏感性等要求。近年来，研究者们逐渐地使用混沌系统来构建更安全的哈希算法，在对混沌哈希算法的研究中，最为常用的混沌系统多数为低维混沌系统，但随着混沌研究的不断进展，研究者发现低维混沌系统由于迭代方式简单、满映射区间小等原因已经不足以支撑哈希算法的安全性，进而转向研究并应用高维混沌系统[5]。三维Lorenz混沌系统具有复杂的系统结构使输出更难预测，同时应用3个混沌使应用更加灵活，3个初值和3个参数构成的解空间大大高于低维混沌，由于具有更高的维数和复杂程度使其具有更为优异的动力学特性[6]。笔者为了进一步增强BLAKE哈希算法的安全性，使用优化的轮函数和高维Lorenz混沌系统共同构建压缩函数，根据混沌系统对参数具有很高的敏感性，扩大压缩函数混淆和扩散的范围，增强算法的安全性。

1 预备知识

1.1 BLAKE哈希函数

BLAKE算法以安全性强、效率高等优势，于2012年被美国国家标准与技术研究所(National institute of standards and technology，NIST)征集并入选为SHA-3的最终决赛轮算法之一。BLAKE算法内部采取的局部宽管道结构如图1所示，使用HAIFA迭代框架[7]，其主要思想是在压缩过程中引入盐值和计数值两个额外的参数。该算法压缩函数是基于ChaCha[8]核心函数设计，内部的运算主要是异或、模加和循环移位。

图1 BLAKE算法宽管道结构Fig. 1 Wide pipeline structure of BLAKE algorithm

BLAKE算法家族有BLAKE-224、BLAKE-256、BLAKE-384和BLAKE-512四种哈希算法。各个算法的基本原理均相同，只是在消息摘要值的长度、部分输入输出参数、循环计算轮数和循环移位数等方面略有不同，摘要输出的长度越长，则安全性越高、效率越低。从安全和效率综合考虑后，文中主要研究的算法是BLAKE-256。

1.2 Lorenz混沌系统

Lorenz混沌系统是一个经典的三维连续混沌系统，是气象学家Lorenz在1963年研究气象学时发现的，其微分方程形式的数学表达式为：

(1)

式中,a、b、c——Lorenz混沌系统的控制参数，一般采用的典型取值为a=10、b=28、c=8/3。在保证a和c不变的前提下，b>27.74时，Lorenz混沌系统处于混沌运动状态。

2 BLAKE哈希算法

文中哈希算法使用Lorenz混沌迭代和BLAKE算法的轮函数作为主函数，使用盐值和计数器值为参数作为轮函数和Lorenz系统的输入，增加了哈希算法随机性。并对初值和中间变量进行优化，使其在引入混沌迭代情况下保障其算法效率，整个算法的流程如图2所示。

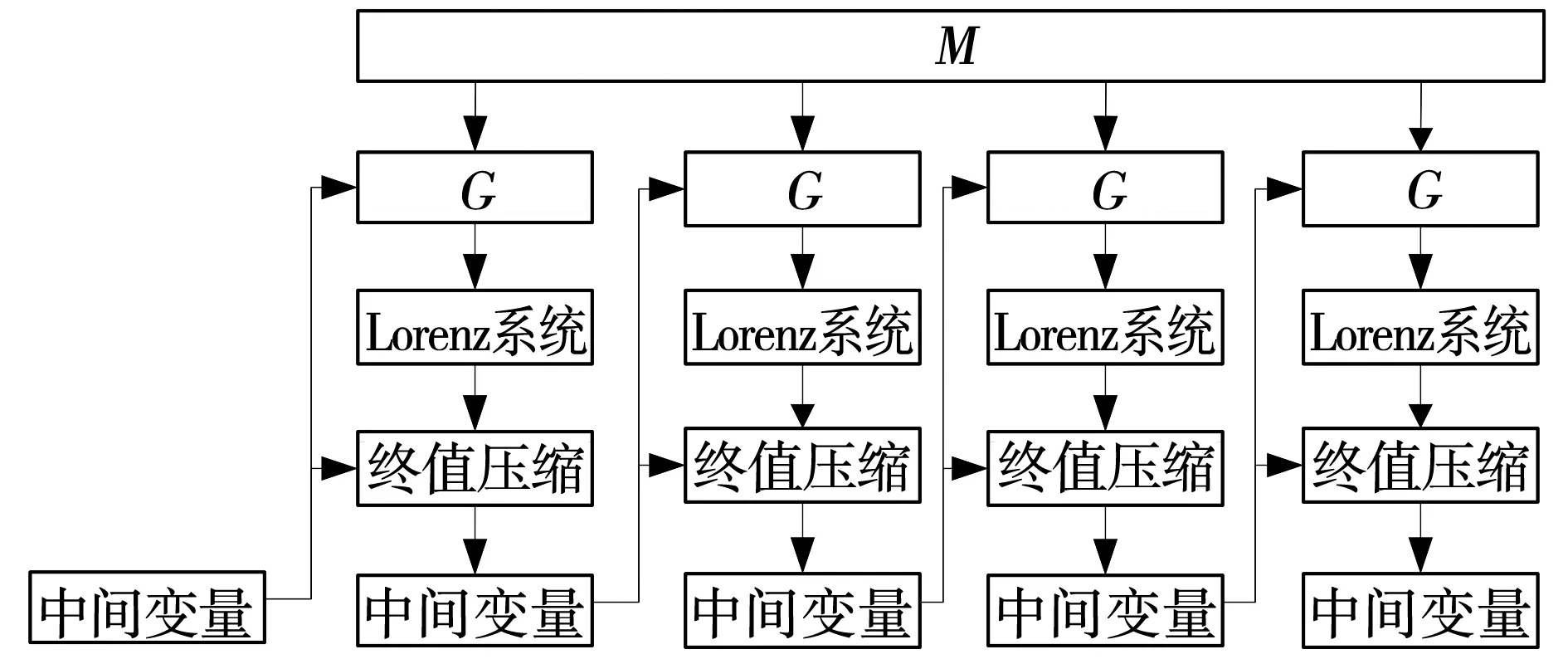
图2 基于Lorenz系统的哈希算法结构 Fig. 2 Structure of hash algorithm based on Lorenz system

首先将消息进行填充，使消息的长度为512比特的整数倍。填充规则有

M←M‖10000…00164，

(2)

式中：M——消息最后不足512比特的数据；

l——消息长度。

先在M后面添加1个1和若干个0，使其消息模512等于447，在添加一个1和64比特表示的消息长度，最后使消息长度为512比特的整数倍。

对算法中有16个中间变量Vi(0≤i≤15)进行赋值，通过下列方程得到

(3)

式中:hi——初始哈希值，(0≤i≤7)；

ci——常数，皆为固定数值，(0≤i≤7)；

ti——计数器，由消息原始长度与填充后长度的累加得到，(0≤i≤1)；

si——盐值，随机赋值生成，(0≤i≤3)。

初始化后得到的16个变量Vi作为轮函数G的输入，总计循环14轮，分别为

G0(V0,V4,V8,V12)G1(V1,V5,V9,V13)G2(V2,V6,V10,V14)G3(V3,V7,V11,V15)G4(V0,V5,V10,V15)G5(V1,V6,V11,V12)G6(V2,V7,V8,V13)G7(V3,V4,V9,V14)，

(4)

式(4)中，每轮的Gi(a,b,c,d)有如下变换

(5)

式中：+——模加运算；

⊕——异或运算；

>>> ——右循环移位操作；

mi、cj——输入的相应消息块或常量。

相比原BLAKE算法的压缩结构上，新轮函数G的前后操作不对称，还增加了循环移位操作，更进一步的增强了轮函数G的扩散性和混淆性。

混沌迭代结构，如图3所示，经过10轮的压缩循环后，将Vi通过Lorenz混沌系统的多次迭代，得出的新值作为新的Vi值。

将Vi通过进制转化为64个ASCII值，为了得到{0,1}之间的初值，对ASCII值进行如下变换

(6)

式中：n——迭代的轮数；

i——初值的序列数；

Vn(i)——第n轮迭代的第i个数。

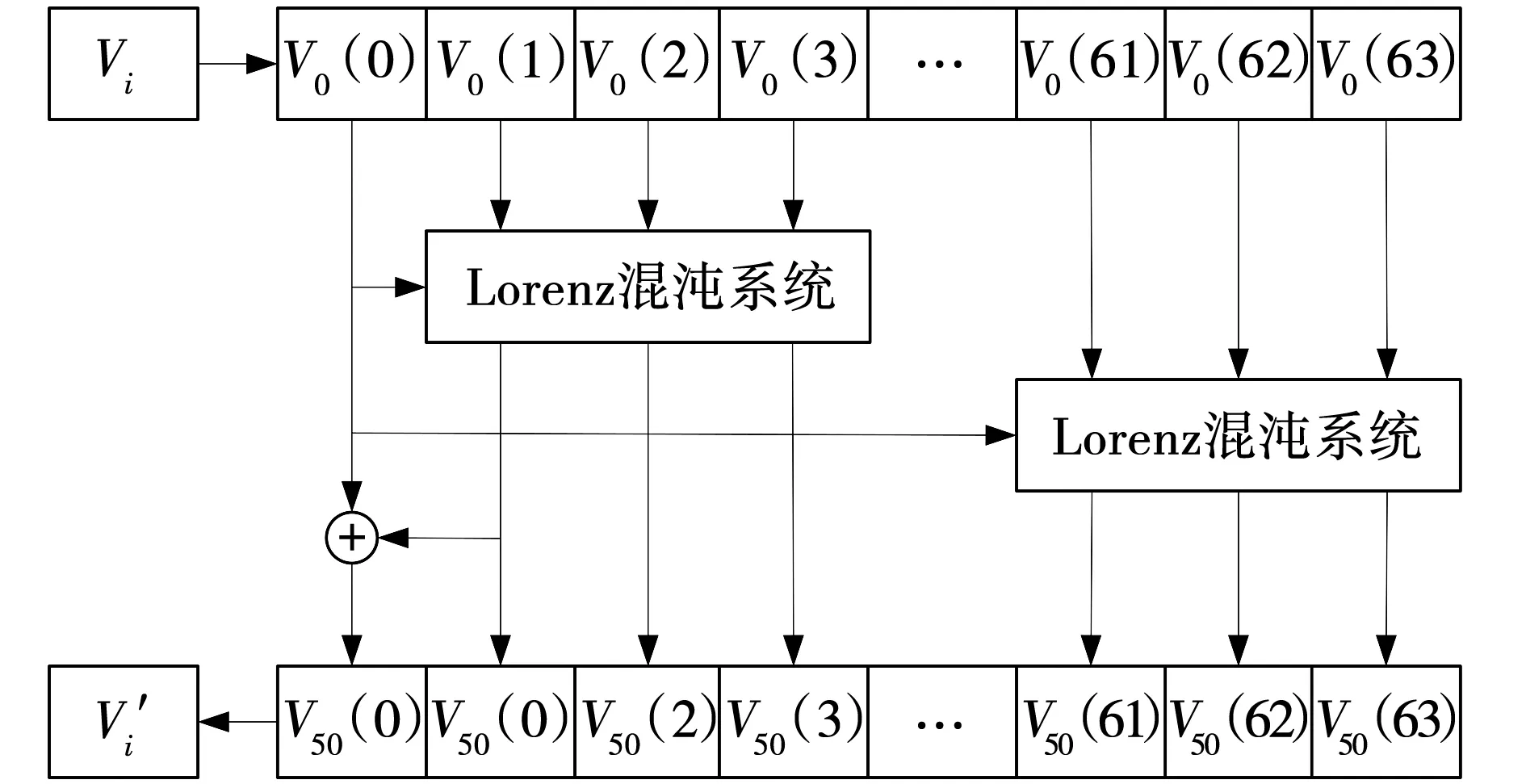
图3 混沌迭代结构Fig. 3 Chaotic iterative structure

第一个值V0(0)作为Lorenz映射的参数b，初值以三个为一组作为Lorenz映射的初值输入，并行混沌迭代50轮，其中第一组Lorenz混沌系统的输出值(V50(1))与V0(0)异或得到V50(0)，然后将所有的值再进行如下逆变换

i=0,1,…,63，

(7)

式中：abs(t)——对t值取其绝对值；

mod——取模运算。

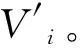
(8)

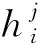
3 BLAKE哈希性能

将从哈希值的分布、初值敏感性、明文与摘要之间的混淆与扩散特性统计和抗碰撞测试等多个方面对所提算法的性能进行分析和讨论。

3.1 哈希值分布

输出哈希的均匀分布是哈希函数重要的安全功能之一。为了测试哈希函数的分布性，采用一条由随机字符组成的消息；将其转换为ASCII值并在图4中进行描述。采用文中的算法得到其哈希值，在图5中以十六进制格式显示。从结果可以看出哈希值分布均匀，明文基本散布在某一有限的区域内，而得到的哈希值却不规则均匀分布在整个空间。实验结果表明所提的算法有很好的分布性。

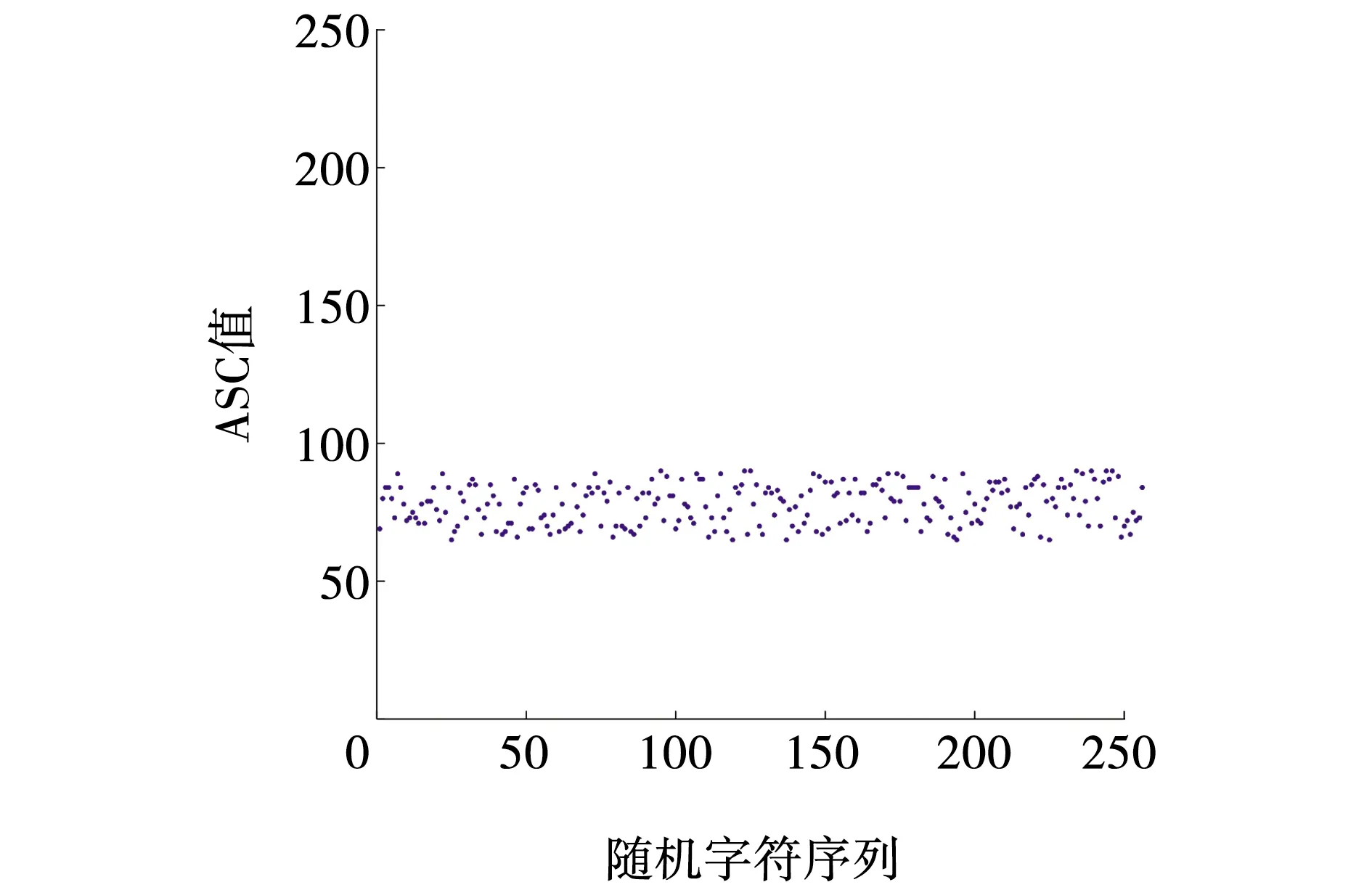
图4 随机字符的分布Fig. 4 Random character distribution

图5 哈希值的分布Fig. 5 Distribution of hash value

3.2 初值敏感性

为了测试所得的哈希值对函数的初值敏感性，任选一段文本：“Chaotic motion is a complex long-term motion unique to deterministic nonlinear dynamic systems.”。按照以下6种情况进行测试：C1：计算给定消息的哈希值。C2：将单词“a”改为“A”。C3：句末的“.”改为“，”。C4：单词“long-term”改为“longterm”。C5：在单词“to”前加个“3”。C6：句末增加一个空格。

对以上消息所得出的256比特值如图6所示。由图6可以看出，消息中的任何位置发生单个位更改，也会导致输出的哈希值发生极大的变化。这证明所提出的方案对于输入消息的改变具有很高的敏感性，很好地满足了加密散列的单向性质。

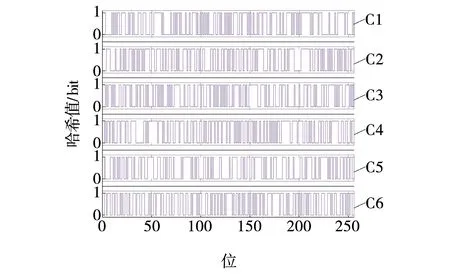
图6 不同情况的哈希值Fig. 6 Hash values in different cases

3.3 混淆与扩散统计

对哈希函数的混淆性和扩散性测试主要是进行雪崩效应测试，测试方案为：随机选取一段消息并计算其哈希值，然后在消息中任意改变1比特，并计算改变后消息的值，比较消息改变前后的结果，得到相应的变化比特数。这样的测试重复进行N=10 000次，得到的变化比特数分布情况如图7所示。结果表明，测试所得的变化比特数均介于101至158之间，且主要集中在理想值128附近。

图7 哈希值变化比特数的分布Fig. 7 Hash value change bit number distribution map

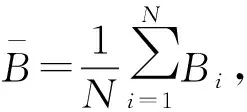
表1 新算法的雪崩特性统计

Table 1 Statistics of avalanche characteristics of newalgorithm

NBminBmaxB-P%ΔBΔP%512105151128.4150.168.053.15 1 024103154128.1650.068.143.182 048103157128.2150.088.213.2110 000101158127.9849.998.053.14

在统计性能的基础上，将文中提出的算法与最近的一些基于混沌的哈希算法进行了比较，结果如表2所示(由于哈希值不同，仅列出了 和 的比较结果)。从表中可以看出文中算法的 最接近理想值50，混淆和扩散性最好， 的值最小，雪崩特性最稳定。

表2N=10 000次数下的统计性能比较

Table 2 Comparison of statistical performance underN=10 000 times%

概率MD5[9]Zhang's[10]Guo's[11]Li's[12]Wang's[13]BLAKE[1]文中算法P50.0249.9649.5350.2150.1150.1249.99ΔP4.424.513.925.814.513.573.15

3.4 抗碰撞

碰撞是指给定不同的明文，经过相同的单向哈希算法得到的哈希值却是相同的。算法的抗碰撞性能越好，表明哈希函数就越可靠。评估哈希函数的抗碰撞性可以通过计算两个消息的哈希值之间的距离，计算公式为：

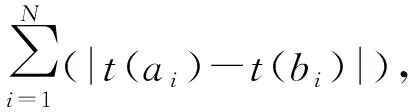
(9)

式中：dh——两个哈希值之间单位字段的绝对差值；

ai、bi——两个哈希值的第i个ASCII字符；

t(x)——将x对应的ASCII字符转化为十进制的值。

文献[14]给出了dh的数学期望

(10)

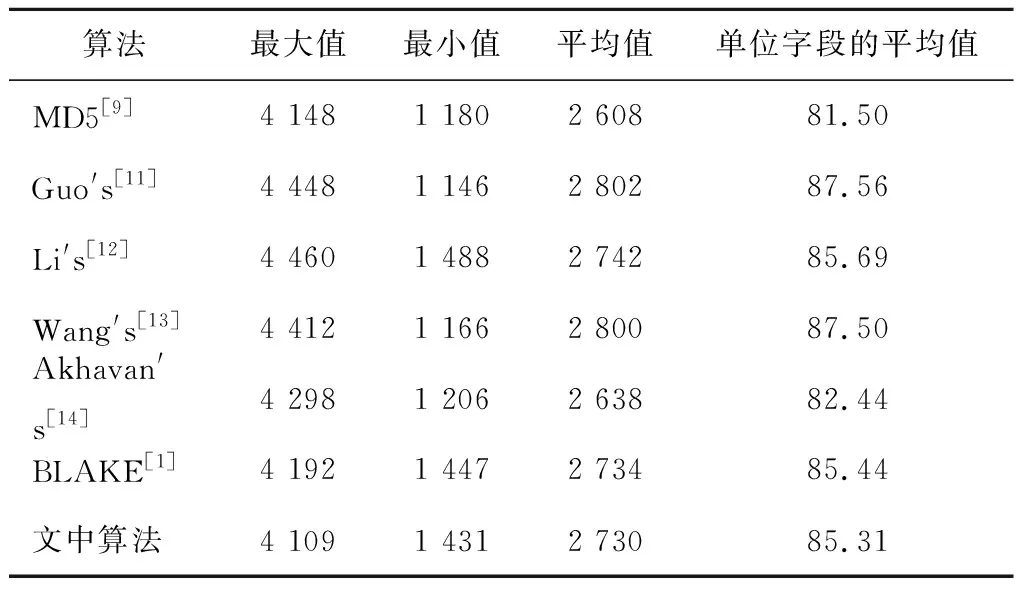
测试N=10 000次时，与其他混沌哈希算法相比较的结果如表3所示。从结果来看，本算法单位字段的值为85.31，最接近于理论平均值85.33，表明新算法的抗碰撞性能最好，能够有效抵抗伪造攻击。

表3N=10 000次数下绝对距离的测试结果

Table 3 Test results of absolute distance atN=10 000 times

算法最大值最小值平均值单位字段的平均值MD5[9]4 1481 1802 60881.50Guo's[11]4 4481 1462 80287.56Li's[12]4 4601 4882 74285.69Wang's[13]4 4121 1662 80087.50Akhavan's[14]4 2981 2062 63882.44BLAKE[1]4 1921 4472 73485.44文中算法4 1091 4312 73085.31

4 结束语

提出了一种基于高维混沌系统的哈希算法，该算法采用BLAKE函数的轮函数和Lorenz混沌迭代作为压缩函数，在循环压缩中增加循环移位运算，保证压缩结构的前后不对称，进一步增强算法的混淆性和扩散性。在Lorenz映射的初始状态中引入中间变量，使每一轮混沌迭代都处于不同的运动状态。最终的哈希值由每一轮混沌迭代后的中间变量、初始哈希、盐值和计数器值计算得到。通过对该算法进行测试分析，结果表明该算法有着良好的分布性和敏感性，相比原BLAKE算法和其他混沌哈希算法，本文算法的混淆性和扩散性的指标更接近理想值，雪崩特性更稳定，抗碰撞攻击的能力也更强。