基于有限元功率流法的轮轨系统能量分布特性研究
2020-07-13周昌盛周华龙杨文茂
周昌盛,周华龙,杨文茂,王 平
(1.中铁二院工程集团有限责任公司地下铁道设计研究院,成都 610031; 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
伴随着我国轨道交通的发展,其产生的振动噪声逐渐影响着沿线居民的生产生活。进入21世纪以来,轨道交通振动噪声污染已成为人们需要重点解决的污染之一。在评价振动特性方面,轨道交通领域中一直采用传统的单因素评价指标(力、加速度、速度、位移)。大量研究表明,振动是以能量的形式在轮轨系统中传递,现有的评价指标具有一定的局限性。
功率流作为一种结合了力与速度两种变量的评价指标,可以从能量的角度评价结构振动特性,在机械、航空与船舶等专业中广泛应用。Goyder和White[1]提出功率流概念,并研究了无限梁和板中的功率流;Park[2]利用功率流方法研究了小阻尼系统高频的振动特性;杨波[3]和沈荣瀛[4]用传递导纳方法对复杂双层隔振系统进行了研究;周保国[5]、吴广明[6]用导纳方法对功率流在浮筏系统中的传递作出了解释;伍先俊[7]对振动功率流的计算方法进行了研究。此外,国内外学者也尝试将功率流方法运用于轨道交通的振动特性研究中。MFM Hussien[8]结合建立的地下隧道内浮置板模型,用平均功率流评价了减振措施的有效性;刘维宁[9]等基于功率流法对梯形轨枕轨道结构的减振性能进行了研究;谷爱军[10]采用导纳形式的功率流,建立了浮置板轨道的振动能量传递分析模型,并推导了输入基础的功率流表达式,探讨了轨道参数对于减振效果的敏感性;陈敏敏[11]利用有限元功率流方法研究了桥梁-承轨台轨道结构的振动特性,并分析了扣件刚度及阻尼变化对钢轨和承轨台输入总功率流的影响;刘鹏辉[12]从振动功率流的角度,建立了轨下-枕下-道砟下垫层及钢轨-浮置板-基础的功率流传递模型,讨论了轨道结构中关键参数对轨道结构功率流的影响。尽管功率流法已在轨道交通中应用,并取得一定的研究成果。然而,上述研究存在以下不足:(1)以上文献只是单纯进行了谐响应分析,并未考虑实际不平顺作用下的随机振动特性;(2)未综合比较加速度、功率流两种指标在评价振动上的差异性;(3)只研究能量在轨道结构中的传递特性,而没有结合车辆子系统研究能量在轮轨耦合系统内的传递及分布规律。
鉴于研究中存在的不足,结合轮轨动力学模型与有限元功率流方法,推导了不平顺激励下输入轮轨系统、车辆子系统(包括各子结构)、轨道子系统的功率流计算公式;计算分析了不平顺激励下能量在轮轨系统中的分布规律,并分别以加速度、功率流为评价指标,比较分析了振动在车辆子系统内的传递及损失规律。
1 功率流方法介绍
1.1 功率流理论介绍
功率流是将物理学中的功率概念应用于振动分析领域,其包含力和速度两个参量,能够直观反映能量的分布及传递规律。输入结构的功率的基本表达式如下
P=F(t)·V(t)
(1)
式中,F(t)为作用于结构某点处的外力,而V(t)为该点处对F(t)所产生的速度响应,均是时间的函数。
对于振动分析来说,平均功率可反映振动的强度,因为在一段时间内的平均功率,比某一时刻的瞬时功率更能反映外部激励注入结构的能量强度,这样就把按时间平均的功率定义为振动功率流,即
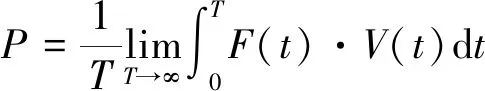
(2)
1.2 有限元功率流法
应用于振动分析领域的功率流方法有多种,包括有限元功率流法、导纳功率流法、波动功率流法及试验功率流法等,各种方法有不同的特点。有限元功率流法是指应用有限元软件计算出各点的应力、速度等响应,根据功率流与力、速度之间的简单关系,研究结构功率流动的方法。该方法的优点是理论简单,只需要通过计算模型或软件计算出的力、速度响应进行后处理分析,即可得到流动到各结构中的功率。随着一些大型计算软件的推广应用,有限元功率流法也得到发展应用。
鉴于工程中多以有限单元法将钢轨进行离散,并进而求解轮轨耦合系统的动力响应。因此,拟将有限元功率流法运用于轮轨系统动力学的研究当中,以功率流为评价指标,从能量的角度分析振动在轮轨系统中的传递及分布规律。
2 轮轨系统动力学模型及功率流理论推导
本章将有限元功率流的思想与传统的轮轨系统动力学理论相结合,推导出输入轮轨系统、车辆子系统(包括各子结构)、轨道子系统功率流的计算公式。
2.1 轮轨系统动力学模型
(1)模型简介
首先运用哈密尔顿原理与车辆-轨道耦合动力学理论,建立了高速列车-轨道垂向耦合动力学模型,用以模拟高速列车-轨道系统垂向受力运动情况[13-15]。模型中车辆子系统由多刚体结构模拟,考虑车体与转向架的沉浮、点头运动,以及车轮的沉浮运动;鉴于目前高铁中主推CRTSⅢ型板式无砟轨道,轨道弹性几乎由扣件系统提供,因此轨道系统采用单层离散点支承模型,并利用有限单元法对其进行离散,模型如图1所示。
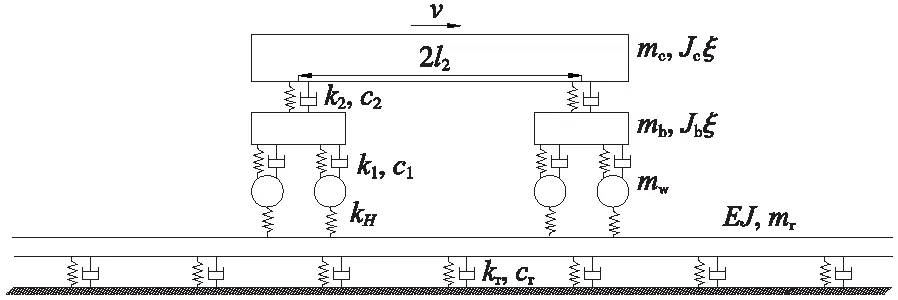
图1 全车-单层弹性点支承轨道平面模型
(2)系统垂向振动方程组的建立及求解
基于哈密尔顿原理,根据系统的总动能、总势能及相应的虚功,结合计算机中的对号入座法则[16],可以很方便地建立车辆-轨道系统振动方程组
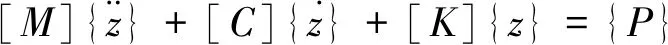
(3)
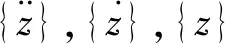
模型建立后,首先采用Wilson-θ法起步运算,然后再采用Park法求解振动方程组,其中Δt=1 ms,θ=1.4。
2.2 功率流计算公式推导
(1)轮轨系统内各子系统的输入功率流
轮轨系统中,车辆与轨道为多点接触,对于车辆子系统和轨道子系统而言都是多点激励。输入车辆子系统、轨道子系统的功率流Pc及Pg见式(4)、式(5)。
Pc=[F][Vl]
(4)
Pg=[F][Vg]
(5)
其中
[F]=[F11…F1m…Fn1…Fnm]
[Vl]=[V11…V1m…Vn1…Vnm]T
[Vg]=[Vg11…Vg1m…〗Vgn1…Vgnm]T
上述表达式中,Fnm为作用在第n节车第m个轮对的轮轨力;Vnm为第n节车第m个轮对的垂向振动速度;Vgnm为第n节车第m个轮对接触点处钢轨的垂向振动速度。
输入轮轨系统的功率流为Pc与Pg之和。
(2)车辆子系统内各子结构的输入功率流
输入轮对的功率流即输入车辆子系统的功率流;
输入转向架的功率流为
PZ=[F1][Vz]
(6)
[F1]=[Fz11…Fz1m…Fzn1…Fznm]
[Vz]=[Vz11…Vz1m…Vzn1…Vznm]
输入车体的功率流为
PB=[F2][Vb]
(7)
[F2]=[Fb11…Fb1l…Fbn1…Fbnl]
[Vb]=[Vb11…Vb1l…Vbn1…Vbnl]
式中,Fznm为第n节车第m个轮对传递至转向架的力;Vznm为Fznm作用点处对应的转向架的垂向振动速度(考虑点头作用);Fbnl为第n节车第l个转向架传递至车体的力;Vbnl为Fbnl作用点处对应的车体的垂向振动速度(考虑点头作用)。
3 计算参数及功率流的时频转换
3.1 功率流信号的后处理
利用车辆-轨道耦合动力学模型可以计算得到轮轨系统内各结构的力、速度信号,进而统计得到输入各子系统(子结构)的功率流时域信号。然而,研究表明,经时间平均的功率流更能反映振动的强度[17]。因此,可通过时频转换得出功率流在频域内的大小与分布,具体流程见图2。另外,为直观展示,引入功率电平的概念并采用1/3倍频程的展示方法。

图2 功率流分析流程示意
功率电平是通过计量的功率值与功率为1 mW的零电平功率比较所确定的相对大小值,其数学表达式如下
Pm=10·lg(P/1) dBm
(8)
式中,Pm为功率电平;P为需要计量的绝对功率值,mW;1表示零电平功率为1 mW;dBm表示以1 mW为基准的功率电平分贝值。
3.2 计算参数
计算过程中,车辆采用CRH3型高速列车,其参数见表1[18],行车速度取350 km/h;不平顺激励采用中国高速轨道谱(波长取0.1~200 m),不平顺时域样本如图3所示;轨道结构参数见表2。
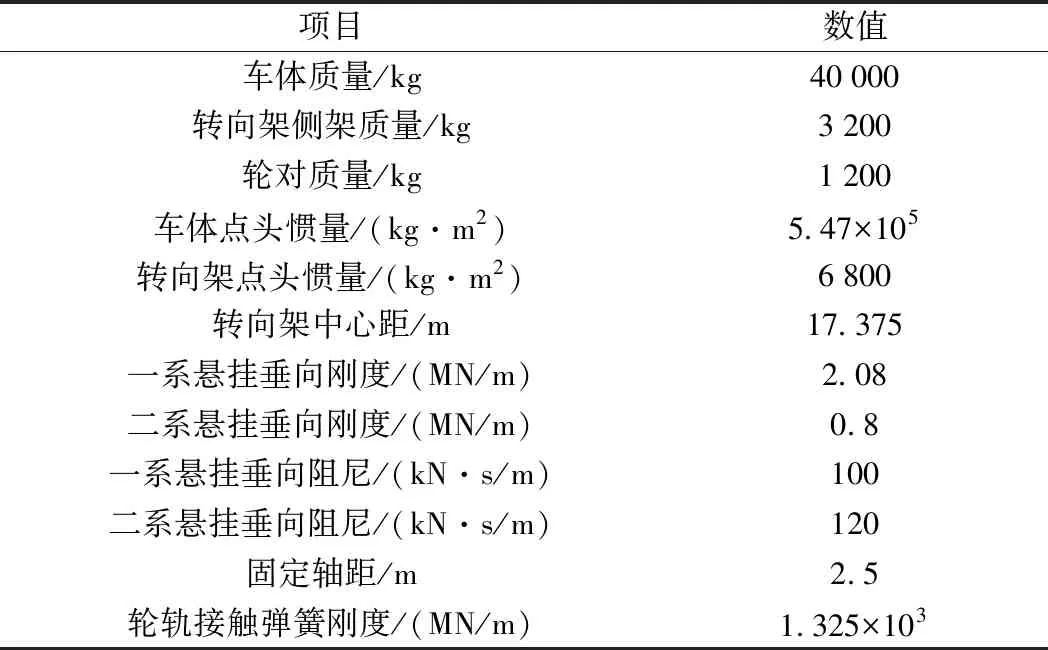
表1 CRH3型高速列车垂向模型参数
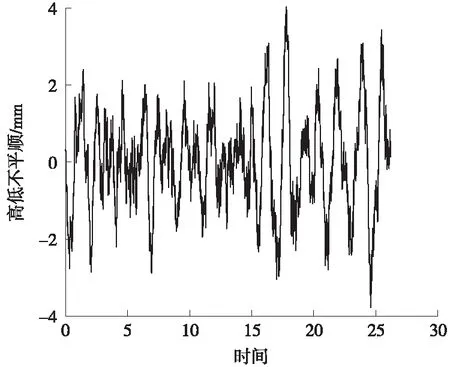
图3 高低不平顺时域样本

>表2 轨道模型参数
4 轮轨系统内能量分布及传递特性分析
以功率流为指标,通过计算并给出车辆子系统、轨道子系统及轮轨系统总输入功率流的大小与分布,进而研究随机振动过程中能量在轮轨系统中的分布规律。另外,分别以加速度及功率流为评价指标,通过计算给出车辆子系统内各子结构的加速度及输入功率流大小与分布,进而分析振动的传递规律[19-20]。
4.1 轮轨系统内功率流分布特性研究
各子系统输入功率流的大小及分布如图4所示。

图4 输入各子系统功率流1/3倍频分布
从图4可见,车辆子系统的输入功率流在0~8 Hz及高于200 Hz的频段内较小,而在8~200 Hz频段范围内取值较大,且在中心频率为63 Hz的频段内有最大功率电平131.3 dBm;轨道系统的输入功率流在0~40 Hz频段内较小,在高于40 Hz的频段范围内较大,且在中心频率为630 Hz的频段内有最大功率电平136.9 dBm。
另外,比较各曲线可以发现:轮轨系统的输入功率曲线与车辆子系统的输入功率曲线在低频阶段几乎重叠,轮轨系统的输入功率曲线在高频阶段与轨道系统的输入功率曲线重叠;中心频率在63 Hz以下时,车辆子系统输入功率曲线高于轨道系统的输入功率曲线,当中心频率高于63 Hz时,则反之。因此,列车运行时产生的低频能量主要输入到车辆子系统中,从而引起车辆子系统的低频响应;高频能量主要传递至轨道系统,引起轨道结构的高频振动。
4.2 轮轨系统内功率流传递关系研究
分别以加速度及功率流为评价指标,分析振动在车辆子系统内的传递规律,并比较两种评价指标的异同。
(1)加速度指标
图5为随机振动过程中,车辆子系统内的车体、转向架、轮对的竖向加速度振级。图6为转向架与车体的振动加速度衰减幅度。

图5 1/3倍频未计权的车体、转向架、轮对竖向振动加速度级
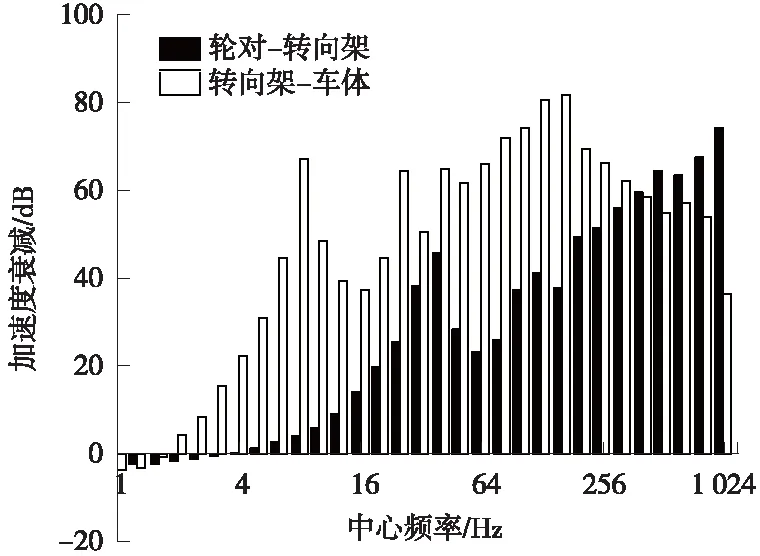
图6 轮对-转向架-车体振动加速度衰减幅度
由图5可知,轮对(转向架、车体)垂向振动加速度在中心频率为63 Hz(63,16 Hz)频段内出现极值,为128.5 dB(105.2,63.3 dB)。轮对加速度在高于16 Hz频率范围内较大,转向架振动加速度主要分布在16~80 Hz,而车体振动加速度主要分布在20 Hz以下的低频范围。轮轨相互作用过程中,2 Hz以上各频带范围内,车辆子系统内各部件的振动强度自下而上发生显著的衰减。2 Hz以下各频带范围内,出现车体加速度大于转向架、轮对加速度的情况,其原因是加速度经过一系、二系悬挂时,加速度主频会向低频小幅偏移,而2 Hz以下范围内各频带带宽较小,最终导致车体加速度在该频带内有效值显著增大。
由图6可知,经一系悬挂的减振,转向架的振动强度在16 Hz以上的中高频发生明显减弱,最高的在1 000 Hz附近衰减74.3 dB,而在16 Hz以下的低频部分变化不大;经二系悬挂的减振,车体的振动强度在全频范围内降低,最高的在160 Hz频段衰减81.7 dB。
(2)功率流指标
以功率流为评价指标研究振动的传递特性,计算并得出的传递至车辆子系统内各部件功率流的大小如图7所示。统计的车辆子系统输入功率流在流经一系、二系悬挂时各频段的损耗幅度如图8所示。
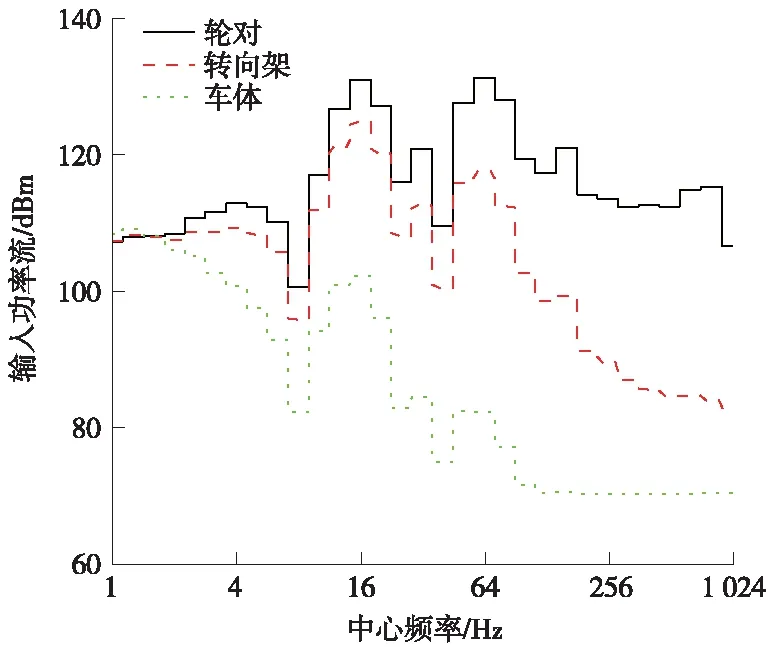
图7 车体、转向架、轮对的输入功率流

图8 轮对-转向架-车体振动功率流衰减幅度
由图7可知,轮对(转向架、车体)的输入功率流在中心频率为63 Hz(16,1.25 Hz)的频段内出现最大值,为131.3 dBm(124.8,109.1 dBm)。具体的,输入轮对的功率流在全频域范围内均保持较大值,转向架的输入功率流主要分布在250 Hz以下的中低频范围,而车体的输入功率流主要分布在20 Hz以下的低频范围。2 Hz以上各频带范围内,传递至车辆子系统的功率流由下至上(轮对-转向架-车体)在全频范围内发生衰减。2 Hz以下各频带范围内,出现车体输入功率流大于转向架、轮对输入功率流的情况,其原因与图5中出现情况类似。
由图8可知,输入功率流流经一系悬挂时,高频范围的能量得到消耗,其中在中心频率为800 Hz的频段内功率流损耗31.3 dBm;输入功率流流经二系悬挂时,在全频域范围内出现损耗,其中在中心频率为50 Hz频段内功率流损耗33.6 dBm。
通过对比图5与图7可见:车体的加速度强度与输入功率流频域分布总体一致,而轮对及转向架的振动加速度强度与输入功率流分布并不相符。这是由于传递至轮对(转向架)的能量,一部分留在轮对(转向架)处,引起该结构的振动,另一部分则传递至转向架(车体)处;而输入车体的能量则由于不能继续往下传递,则几乎所有的能量都通过振动的形式消耗。
通过对比图6与图8可以发现,经一系(二系)悬挂减振后,结构间的振动加速度衰减与能量消耗分布并不统一,说明了加速度指标并不能体现振动在结构间的实际传递与消耗情况。
综上所述,功率流评价指标直观地给出结构的输入能量及结构间能量的传递、消耗情况,而加速度则只能反映对象部件的振动强度。因此,在进行结构的减振、隔振等分析研究时,推荐采用功率流指标;而在评价结构振动强度时,建议使用加速度指标。
5 结论与建议
基于目前轨道交通领域振动评价指标的局限性,将有限元功率流方法与传统的轮轨系统动力学理论相结合,引入功率流指标,从能量的角度分析不平顺激励下轮轨系统内振动的分布及传递规律,并对比分析了加速度与功率流两种指标的差异性。得到如下结论。
(1)列车垂向振动中产生的低频(低于63 Hz)能量主要流入车辆子系统,引起车辆子系统低频振动响应,而高频(高于63 Hz)能量则传递至轨道系统,引起轨道结构的高频振动。
(2)功率流指标能直观给出振动能量在结构中的传递及分配规律,适合于减振、隔振措施分析研究;而加速度指标能直观地反映作用于指定结构的振动能量大小,适合作为减振效果的评价分析。
